Samacheer Kalvi 7th Maths Guide Term 3 Chapter 3 இயற்கணிதம் Ex 3.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 7th Maths Guide Pdf Term 3 Chapter 3 இயற்கணிதம் Ex 3.1 Textbook Questions and Answers, Notes.

TN Board 7th Maths Solutions Term 3 Chapter 3 இயற்கணிதம் Ex 3.1

Question 1.
கோடிட்ட இடங்களை நிரப்பு.

i) (p – q)² = ________
விடை :
p² – 2pq + q²

ii) (x + 5) மற்றும் (x – 5) இன் பெருக்கற்பலன் _________
விடை :
x² – 25

iii) x² – 4x + 4 இன் காரணிகள் __________
விடை :
(x – 2) மற்றும் (x – 2)

iv) 24ab²c² என்ற காரணியின் பெருக்கற்பலன் _________
விடை :
2 × 2 × 2 × 3 × a × b × b × c × c

Question 2.
பின்வரும் கூற்றுகள் சரியா, தவறா எனக் கூறுக.

i) (7x + 3) (7x – 4) = 49x² – 7x – 12.
விடை :
சரி

ii) (a – 1)² = a² – 1.
விடை :
தவறு

iii) (x² + y²) (y² + x²) = (x² + y²)².
விடை :
சரி

iv) 8pq இன் காரணி 2p ஆகும்
விடை :
சரி

Question 3.
பின்வருவனவற்றை அவற்றின் காரணகளின் பெருக்கற்பலனாக எழுதுக.

i) 24 ab²c²
= 2 × 2 × 3 × 3 × a × b × c

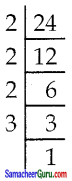
ii) 36 x³y²z
= 2 × 2 × 3 × 3 × x × x × y × y × z

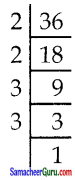
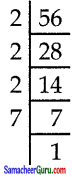
iii) 56 mn²p²

= 2 × 2 × 2 × 7 × m × n × n × p × p

Question 4.
(x + a)(x + b)= x² + x(a + b) + ab , என்னும் முற்றொருமையைப் பயன்படுத்திப், பின்வருவனவற்றின் பெருக்கற்பலனைக் காண்க.

இங்கு a = 3, b = 7, x = x

i) (x + 3) (x + 7)
= x² + x(3 + 7) + 3 × 7
= x² + 10x + 21

இங்கு x = 6a, a = 9, b = -5

ii) (6a + 9)(6a – 5)
= (6a)² + (6a) (9 – 5) + 9(-5)
= 36a² + 24a – 45

இங்கு x = 4x, a = 3y, b = 5y

iii) (4x + 3y)(4x + 5y)
= (4x)² + 4x(3y + 5y) + 3y × 5y
= 16x² + 32xy + 15y²

இங்கு x = pq, a = 8, b = 7

iv) (8 + pq)(pq + 7)
= (pq)² + (pq) (8+7) + (8 × 7)
= p²q² + 15pq + 56

Question 5.
முற்றொருமைகளைப் பயன்படுத்திப் பின்வரும் கோவைகளை விவரி.

i) (2x + 5)²
(a+b)² = a² + 2ab + b²
இங்கு a= 2x b = 5
(2x + 5)² = (2x)² + 2(2x) (5) = (5)²
= 4x² + 20x + 25

ii) (b – 7)²
(a – b)² = a² – 2ab + b²
இங்கு a = b b = 7
(b – 7)² = (b)² – 2(b)(7) = (7)²
= b² – 14b + 49

iii) (mn + 3p)²
(a+b)² = a² + 2ab + b²
இங்கு a = mn b= 3p
(mn + 3p)² = (mn)² + 2(mn)(3p) + (3p)²
= m²n² + 6mnp + 9p²

iv) (xyz – 1)²
(a – b)² = a² – 2ab + b²
(xyz – 1)² = (xyz)² – 2(xyz) (1) + (1)²
= x²y²z² – 2xyz + 1

Question 6.
(a + b)(a – b) = a² – b² என்னும் முற்றொருமையைப் பயன்படுத்திப் பின்வருவனவற்றின் பெருக்கற்பலனைக் காண்க.

i) (p + 2)(p – 2)
(a+b) (a-b) = a² – b²
(p+2) (p-2) = (p)² – (2)²
= p² – 4

ii) (1 + 3b)(3b – 1)
(a+b) (a-b) = a² – b²
(3b + 1) (3b – 1) = (3b)² – (1)²
= 9b² -1

iii) (4 – mn)(mn + 4)
(a – b) (a + b) = a² – b²
(4 – mn) (4+mn) = (4)² – (mn)²
= 16 – m²n²

iv) (6x + 7y)(6x – 7y)
(a + b) (a – b) = a² -b²
(6x + 7y) (6x-7y) = (6x)² – (7y)²
= 36x² – 49y²

Question 7.
பொருத்தமான முற்றொருமைகளைப் பயன் படுத்திப் பின்வருவனவற்றின் மதிப்பைக் காண்க.

i) 51²
(a + b)² = a² + 2ab + b²
(51)² = (50 + 1)² = (50)² + 2 (50)(1) + (1)²
= 2500 + 100 + 1 = 2601

ii) 103²
(a + b)² = a² + ab + b²
(103)² = (100 + 3)² = (100)² + 2(100)(3) + (3)²
= 10000 + 600 + 9 = 10609

iii) 998²
(a – b)² = a² – 2ab + b²
(998)² = (1000 – 2)²
= (1000)² – 2(1000)(2) + (2)
= 1000000 – 4000 + 4
= 1000004 – 4000 = 996004

iv) 47²
(a – b)² = a² – 2ab + b²
472 = (50 – 3)² = (50)² – 2(50)(3) + (3)²
= 2500 – 300 + 9
= 2509 – 300 = 2209

v) 297 × 303
(a – b) (a+b) = a² – b²
(297) × (303) = (300-3) (300+3)
= (300)² – (3)²
= 90000 – 9 = 89991

vi) 990 × 1010
(a – b) (a + b) = a² – b²
(990) × (1010) = (1000 – 10) (1000 + 10)
= (1000)² – (10)²
= 1000000 – 100 = 999900

vii) 51 × 52
(x + a) (x + b) = x² + x(a + b) + ab
(51) × (52) = (50 + 1) (50 + 2)
= (50)² + 50(1 + 2) = (1 × 2)
= 2500 + 150 + 2 = 2652

Question 8.
சுருக்குக : (a+b)² – 4ab
(a + b)² – 4ab
= a² + 2ab + b² – 4ab
= a² – 2ab + b²
= (a – b)²

Question 9.
(m – n)² + (m + n)² = 2(m² + n²) என நிறுவுக
இடப்பக்கம் = (m – n)² + (m + n)²
= m² – 2mn + b² + m² + 2mn + n²
= 2m² + 2n²
= 2(m² + n²) = வலப்பக்கம்

Question 10.
a + b = 10 மற்றும் ab = 18 எனில் a² + b² இன் மதிப்பைக் காண்க.
a + b = 10 ab = 18
a² + b² = (a + b)² – 2ab
= (10)² – 2(18) = 100 – 36 = 64

Question 11.
a² – b² = (a + b)(a – b) என்னும் முற்றொருமையைப் பயன்படுத்திப் பின்வரும் இயற்கணிதம் கோவைகளைக் காரணிப்படுத்துக.

i) z² – 16
= z² – 4²
= (z + 4) (z -4)

ii) 9 – 4y²
= (3)² – (2y)²
= (3 + 2y) (3 – 2y)

iii) 25a² – 49b²
= (5a)² – (7b)²
= (5a + 7b) (5a – 7b)

iv) 4⁴ – y⁴
= (x²)² – (y²)²
= (x² + y²) (x² – y²)
= (x² + y²) (x + y) (x – y)

Question 12.
பொருத்தமான முற்றொருமைகளைப் பயன்படுத்திப் பின்வருவனவற்றைக் காரணிப்படுத்துக.

i) x² – 8x + 16
a = x, b = 4
(a – b)² = a² – 2ab + b²
x² – 8x + 16 = x² – 2(x) (4) + 4²
= (x – 4)²

ii) y² + 20y + 100
(a + b)² = a² + 2ab + b²
a = y, b = 10 y² + 20y + 100
= y² + 2(y)(10) + 10²
= (y + 10)²

iii) 36m² + 60m + 25
(a + b)² = a² + 2ab + b²
a = 6m, b = 5
36m² + 60m + 25
= (6m)² + 2(6m)(5) + 5²
= (6m + 5)²

iv) 64x² – 112xy + 49y²
(a – b)² = a² – 2ab + b²
a = 8x, b = 7y
64x² – 112 xy + 49y²
= (8x)² – 2(8x)(7y) + (7y)² = (8x – 7y)²

v) a² + 6ab + 9b² – c²
(a + b)² = a² + 2ab + b²
a² – b² = (a + b)(a – b)
a² + bab + 9b² – c² = a² + 2(a)(3b) + (3b)² – c²
= (a+3b)² – c²
= (a + 3b + c) (a + 3b – c)

கொள்குறி வகை வினாக்கள்

Question 13.
a + b = 5 மற்றும் a² + b² = 13 எனில் ab =_______
i) 12
ii) 6
iii) 5
iv) 13
விடை :
ii) 6

Question 14.
(5 + 20)(-20 – 5) = _______
i) – 425
ii) 375
iii) – 625
iv) 0
விடை :
iii) – 625

Question 15.
x² – 6x + 9 இன் காரணிகள்
i) (x – 3)(x – 3)
ii) (x – 3)(x + 3)
iii) (x + 3)(x + 3)
iv) (x – 6)(x + 9)
விடை :
i) (x – 3)(x – 3)

Question 16.
ax²y , bxy² மற்றும் cxyz ஆகிய இயற்கணிதக் கோவைகளின் பொதுக் காரணி
i) x²y
ii) xy²
iii) xyz
iv) xy
விடை :
iv) xy