Students can Download Maths Chapter 5 Statistics Ex 5.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 5 Statistics Ex 5.4
Miscellaneous Practice problems
Question 1.
Arithmetic mean of 15 observations was calculated as 85. In doing so an observation was wrongly taken as 73 for 28. What would be correct mean?
Solution:

85 × 15 = sum of 15 observations
1275 = sum of 15 observations
Wrong observation = 73
Correct observation = 28

Correct mean = 82
![]()
Question 2.
The median of 25,16,15,10, 8, 30.
Solution:
Arranging is ascending order : 8, 10, 15, 16, 25, 30
Here n = 6, even
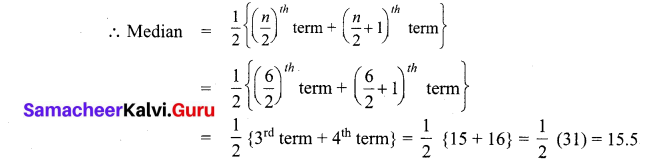
∴ Median = 15.5
Question 3.
Find the mode of 2, 5, 5, 1, 3, 2, 2, 1, 3, 5, 3.
Solution:
Arranging the data in ascending order: 1, 1, 2, 2, 2, 3, 3, 3, 5, 5, 5
Here 2, 3 and 5 occurs 3 times each.
Which is the maximum number of times.
∴ Mode is 2, 3 and 5.
![]()
Question 4.
The marks scored by the students in social test out of 20 marks are as follows.
12, 10, 8, 18, 14, 16. Find the mean and the median?
Solution:
Arranging the given data in ascending order: 8, 10, 12, 14, 16, 18.

There are n = 6 observations, which is even

Question 5.
The number of goals scored by a football team is given below.
Find the mode and median for the data of 2 ,3, 2, 4, 6, 1, 3, 2, 4, 1, 6.
Solution:
Arranging the given data in ascending order: 1, 1, 2, 2, 2, 3, 3, 4, 4, 6, 6
Clearly 2 occurs at the maximum of 3 times and so mode = 2
Here number of data of data n = 11, odd.
∴ Median = (\(\frac { n+1 }{ 2 } \))th term
= (\(\frac { 11+1 }{ 2 } \))th
term = (\(\frac { 12 }{ 2 } \))th term
= 6th term
Median = 3
![]()
Question 6.
Find the mean and mode of 6, 11, 13, 12, 4, 2.
Answer:
Arranging is ascending order : 2, 4, 6, 11, 12, 13

Mean = \(\frac { 48 }{ 6 } \) = 8
All observation occurs only once and so there is no mode for this date.
![]()
Challenge Problems
Question 1.
The average marks of six students is 8. One more student mark is added and the mean is still 8. Find the student mark that has been added.
Solution:

Sum of observation = 6 × 8 = 48
If one more mark is added then number of observations = 6 + 1 = 7
Let the number be x
Still average = 8
∴ 8 = \(\frac { 48+x }{ 7 } \)
48 + x = 7 × 8
48 + x = 56
48 + x = 56 – 48
x = 8
∴ The number that is added = 8
![]()
Question 2.
Calculate the mean, mode and median for the following data: 22, 15, 10, 10, 24, 21.
Solution:
Arranging in ascending order: 10, 10, 15, 21, 22, 24

Here n = 6, even
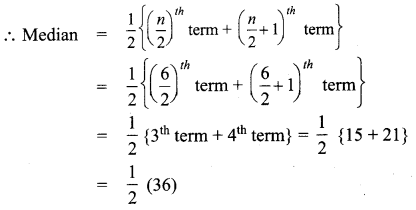
∴ Median = 18
Clearly the data 10 occurs maximum number of times and so 10 is the mode.
∴ Mode = 10
Question 3.
Find the median of the given data: 14, -3, 0, -2, -8, 13, -1, 7.
Solution:
Arranging the data is ascending order: -8, -3, -2, -1, 0, 7, 13, 14
Here number of data n = 8, even
∴ Median

∴ Median = – 0.5
![]()
Question 4.
Find the mean of first 10 prime numbers and first 10 composite numbers.
Solution:
First 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29

Mean = 12.9
Mean of first 10 prime numbers = 12.9
First 10 composite numbers are 4, 6, 8, 9, 10, 12, 14, 15, 16, 18
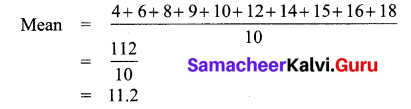
Mean of first 10 composite numbers = 11.2