Students can Download Maths Chapter 1 Number System Ex 1.6 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 1 Number System Ex 1.6
Miscellaneous Practice Problems
Question 1.
What should be added to -1 to get 10?
Solution:
(-1) + a number = 10
∴ The number = 10 + 1 = 11
Question 2.
![]()
Solution:
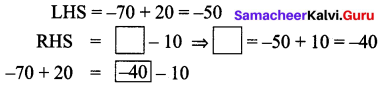
Question 3.
Substract 94860 from (-86945)
Solution:
-86945 – (94860) = -86945 + (Additive inverse of 94860)
= -86945 + (-94860) = -1,81,805
Question 4.
Find the value of (-25) + 60 + (-95) + (-385)
Solution:
(-25) + 60 + (-95) + (-385) = 35 + (-95) + (-385) = -60 + (-385) = -445
![]()
Question 5.
Find the sum of (-9999) (-2001) and (-5999).
Solution:
(-9999) + (-2001) + (-5999) = -12,000 + (-5999) = -17,999
Question 6.
Find the product of (-30) × (-70) × 15.
(-30) × (-70) × 15 = (+2100) × 15 = 31,500
Question 7.
Divide-72 by 8.
Solution:
\(\frac{-72}{8}\) = -9
Question 8.
Find two pairs of integers whose product is +15.
Solution:
(i) (+3) × (+5)
(ii) (-3) × (-5)
Question 9.
Check the following for equality.
(i) (11 + 7) + 10 and 11 + (7 + 10)
(ii) (8 – 13) × 7 and 8 – (13 × 7)
(iii) [(-6) – (+8)] × (-4) and (-6) – [8 × (-4)]
(iv) 3 × [(-4) + (-10)] and [3 × (-4) + 3 × (-10)]
Solution:
(i) LHS = (11 + 7) + 10 = 18 + 10 = 28
RHS = 11 + (7 + 10)
= 11 + (17) = 28
LHS = RHS
∴ (11 + 7) + 10 = 11 + (7 + 10)
(ii) LHS = (8 – 13) × 7 = -5 × 7 = -35
RHS = 8 – (13 × 7) = 8 – 91 = -83
LHS ≠ RHS
∴ (8 – 13) × 7 ≠ 8 – (13 × 7)
(iii) LHS = [(-6) – (+8)] × (-4) = [(-6) + (-8)] × (-4) = (-14) × (-4) = +56
RHS = (-6) – [8 × (-4)] = -6 – (-32)
= -6 + (+32) = +26
LHS ≠ RHS
∴ [(-6) – (+8)] × (-4) ≠ (-6) – [8 × (-4)]
(iv) LHS = 3 × [(-4) + (-10)] = 3 × (-14) = -42
RHS = [3 × (-4) + 3 × (-10)] = (-12) + (-30) = -42
LHS = RHS
3 × [(-4) + (-10)] = [3 × (-4) + 3 × (-10)]
![]()
Question 10.
Kalaivani had ₹ 5000 in her bank account on 01.01.2018. She deposited ₹ 2000 in January and withdrew ₹ 700 in February. What was Kalaivani’s bank balance on 01.04.2018, if she deposited ₹ 1000 and withdraw ₹ 500 in March.
Solution:
Initial bank balance = ₹ 5000 ; Total deposits: January : ₹ 2000 ; March : ₹ 1000
Total deposits upto March = ₹ 5000 + ₹ 2000 + ₹ 1000 = ₹ 8000
Amount withdrawn: February : ₹ 700 (-)
March : ₹ 500 (-)
∴ Total amount withdrawn = (-700) + (-500) ₹ -1200
Net bank balance = ₹ 8000 – ₹ 1200 = ₹ 6800
Question 11.
The price of an item x increases by ₹ 10 every year and an item y decreases by ₹ 15 every year. If in 2018, the price of x is ₹ 50 andy is ₹ 90, then which item will be costlier in the year 2020?
Solution:
Amount increases for x every year = ₹ 10.
Price ofx in 2018 = ₹ 50 ; Price of x in 2019 = ₹ 50 + ₹ 10 = ₹ 60
Price of x in 2020 = ₹ 60 + ₹ 10 = ₹ 70 Amount decreases for y per year = ₹ 15
Price of y in 2018 = ₹ 90
Price of y in 2019 = ₹ 90 – ₹ 15 = ₹ 75
Price of y in 2020 = ₹ 75 – ₹ 15 = ₹ 60
Here 70 > 60. Item x will costlier in year 2020.
Question 12.
Match the statements in Column A and Column B.
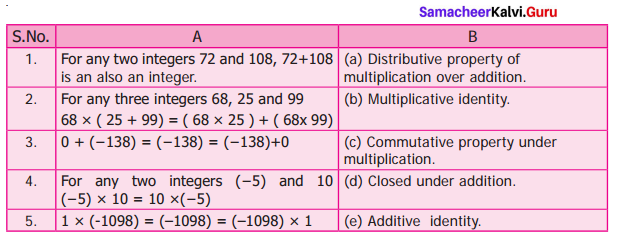
Solution:
1. – d
2. – a
3. – e
4. – c
5. – b
Challenge Problems
Question 13.
Say True or False.
(i) The sum of a positive integer and a negative integer is always a positive integer.
(ii) The sum of two integers can never be zero
(iii) The product of two negative integers is a positive integer.
(iv) The quotient of two integers having opposite sign is a negative integer.
(v) The smallest negative integer is -1.
Solution:
(i) False
(ii) False
(iii) True
(iv) True
(v) False
Question 14.
An integer divided by 7 gives a result -3. What is that integer?
Solution:
According to the problem \(\frac{\text { An integer }}{7}\) = -3
∴ The integer = -3 × 7
The required integer = -21.
![]()
Question 15.
Replace the question mark with suitable integer in the equation.
![]()
Solution:

Question 16.
Can you give 10 pairs of single digit integers whose sum is zero?
Solution:
1 + (-1) + 2 + (-2) + 3 + (-3) + 4 + (-4) + 5 + (-5) = 0
Question 17.
If P = -15 and Q = 5 find (P – Q) – (P + Q).
Solution:
Given P = 15 ; Q = 5
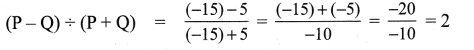
Question 18.
If the letters in the English alphabets A to M represent the number from 1 to 13 respectively and N represents 0 and the letters O to Z correspond from -1 to -12, find the sum of integers for the names given below. For example,
MATH → Sum → 13 + 1 – 6 + 8 = 16
(i) YOUR NAME
(ii) SUCCESS
Solution:
Given

(i) My name LEENA → 12 + 5 + 5 + 0 + 1 = 23
(ii) SUCCESS → (-5) + (-7) + 3 + 3 + 5 + (-5) + (-5)
= -12 + 6 + 5 + (-10) = -6 + 5 + (-10) = (-1) + (-10)
= -11
Question 19.
From a water tank 100 litres of water is used every day. After 10 days there is 2000 litres of water in the tank. How much water was there in the tank before 10 days?
Solution:
Water used for one day = 100 litres.
Water used for 10 days = 100 × 10 = 1000 litres.
After 10 days water left in the tank = 2000 litres
Initially amount of water will be = 2000 + 1000 = 3000 litres
Question 20.
A dog is climbing down into a well to drink water. In each jump it goes down 4 steps. The water level is in 20th step. How many jumps does the dog take to reach the water level?
Solution:
The water in the well is at 20th step.
For each jump the dog goes low 4 steps. 5
∴ Number of jumps the dog to reach the water = \(\frac{20}{4}\) = 5 jumps
![]()
Question 21.
Kannan has a fruit shop. He sells 1 dozen banana at a loss of ? 2 each because it may get rotten next day. What is his loss?
Solution:
1 dozen = 12 bananas
For 1 banana loss = ₹ 2
For 12 bananas loss = ₹ 2 × 12 = ₹ 24
Question 22.
A submarine was situated at 650 feet below the sea level. If it descends 200 feet, what is its new position?
Solution:
Position of submarine = 650 feet below sea level = -650 feet
Again the depth it descends = 200 feet below = – 200 feet
∴ Position of submarine = (-650) + (-200) = -850 feet
The submarine will be 850 feet below the sea level.
Question 23.
In a magic square given below each row, column and diagonal should have the same sum. Find the values of x, y, and z.

Solution:
Column total = Row total = diagonal total
∴ 1 + y + (-6) = (-10) + (-3) + 4
y + (- 5) = -13 + 4
y = -9 + 5
y = -4
So 1 + (-10) + x = y + (-3) + (-2)
-9 + x = (-4) + (-3) + (-2)
-9 + x = -9
x = -9 + 9
x = 0
Now x + (-2) + z = (-10) + (-3) + 4
0 + (-2) + z = (-13) + 4
-2 + z = -9
z = -9 + 2 = -7
z = -7
∴ x = 0, y = -4, z = -7