Students can Download Maths Chapter 4 Direct and Inverse Proportion Ex 4.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 4 Direct and Inverse Proportion Ex 4.2
Question 1.
Fill in the blanks
(i) 16 taps can fill a petrol tank in 18 minutes. The time taken for 9 taps to fill the same tank will be ___ minutes.
(ii) If 40 workers can do a project work in 8 days, then ____ workers can do it in 4 days.
Solutions:
(i) 32
(ii) 80
![]()
Question 2.
6 pumps are required to fill a water sump in 1 hr 30 minutes. What will be the time taken to fill the sump if one pump is switched off?
Solution:
Let x be the required time taken

Time taken in minutes 1 hr. 48m
Question 3.
A farmer has enough food for 144 ducks for 28 days. If he sells 32 ducks how long will the food last?
Solution:
Let the required number of days be x.

As the number of ducks decreases the food will last for more days.
∴ They are in inverse proportion. x1y1 = x2y2

The food lasts for 36 days
![]()
Question 4.
It takes 60 days for 10 machines to dig a hole. Assuming that all machines work at the same speed, how long will it take 30 machines to dig the same hole?
Solution:
Let the number of days required be x.

As the number of machines increases it takes less days to complete the work
∴ They are in inverse proportion, x1y1 = x2y2
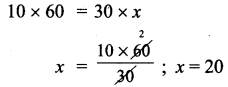
It takes 20 days to dig the hole
Question 5.
Forty students stay in a hostel. They had food stock for 30 days. If the students are doubled then for how many days the stock will last?
Solution:
Let the required number of days be x.

As the number of students increases the food last for less number of days
∴ They are in inverse proportion.
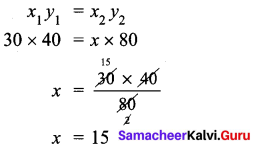
The food stock lasts for 15 days
![]()
Question 6.
Meena had enough money to send 8 parcels each weighing 500 grams through a courier service. What would be the weight of each parcel, if she has to send 40 parcel for the same money?
Solution:
Let the required weight of the parcel be x grams.

As the number of parcels increases weight of a parcel decreases.
∴ They are in inverse proportion.
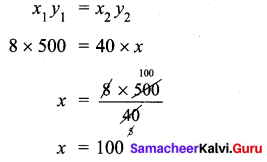
Weight of each parcel = 100 grams
Question 7.
It takes 120 minutes to weed a garden with 6 gardeners. If the same work is to be done in 30minutes, how many more gardeners are needed?
Solution:
Let the, number of gardeners needed be x.

As the number of gardeners increases the time decreases. They are in inverse proportion,
x1y1 = x2y2
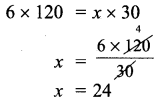
∴ To complete the work in 30 min gardeners needed = 24
Already existing gardeners = 6
∴ More gardeners needed = 24 – 6 = 18
18 more gardeners are needed
![]()
Question 8.
Neelaveni goes by bicycle to her school every day. Her average speed is 12km/hr and she reaches school in 20 minutes. What is the increase in speed, If she reaches the school in 15 minutes?
Solution:
Let the speed to reach school in 15 min be x

∴ They are in inverse proportion x1y1 = x2 y2
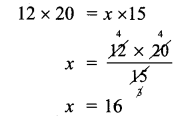
If she reaches in 15 min the speed = 16 km/hr
Already running with 12 km / hr
∴ Increased speed = 16 – 12 = 4km / hr
Increase in speed = 4 km / hr
Question 9.
A toy company requires 36 machines to produce car toys in 54 days. How many machines would be required to produce the same number of car toys in 81 days?
Solution:
Let the required number of machines be x

As the number of machines increases number of days required decreases.

∴ 24 machines would be required
Objective Type Questions
Question 10.
12 cows can graze a field for 10 days. 20 cows can graze the same field for ____ days
(i) 15
(ii) 18
(iii) 6
(iv) 8
Solution:
(iii) 6
Hint:

Question 11.
4 typists are employed to complete a work in 12 days. If two more typists are added, they will finish the same work in days
(i) 7
(ii) 8
(iii) 9
(iv) 10
Solution:
(ii) 8
