Students can Download Maths Chapter 4 Direct and Inverse Proportion Ex 4.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 4 Direct and Inverse Proportion Ex 4.3
Miscellaneous Practice Problems
Question 1.
If the cost of 7 kg of onions is ₹ 84 find the following :
(i) Weight of the onions bought for ₹ 180
(ii) The cost of 3 kg of onions
Solution:
(i) For ₹ 84 weight of onion bought
for ₹ 1 weight of onion bought
∴ For ₹ 180 weight of onion bought w
∴ For ₹ 180 weight of onion bought
(ii) Cost of 7 kg of onions = 15 kg

Question 2.
If C = kd
(i) what is the relation between C and d ?
(ii) Find k when C = 30 and d = 6
(iii) Find C, when d = 10
Solution:
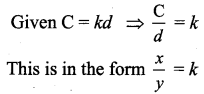
As C increases d also increases
∴ It is direct proportion


Question 3.
Every 3 months Tamilselvan deposits ₹ 5000 as savings in his bank account. In how many years he can save ₹ 1,50,000.
Solution:
Let the number of years required be x.

No. of years and deposit are direct proportion as they both increases simultaneously.

He can save ₹ 1,50,000 in \(7 \frac{1}{2}\) years.
Question 4.
A printer, prints a book of 300 pages at the rate of 30 pages per minute. Then, how long will it take to print the same book if the speed of the printer is 25 pages per minute?
Solution:
Let the required time taken to print be x
As the speed increases time taken to print decreases
∴ They are in inverse proportion
Time taken to print 30 pages = 1 min
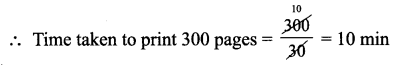

Question 5.
If the cost of 6 cans of juice in ₹ 210, then what will be the cost of 4 cans of juice?
Solution:
Let the cost required be x

As number of cans increases cost also increases.
∴ They are in direct proportion
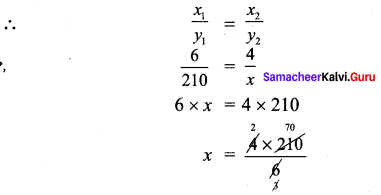
x = 140
Cost of 4 cans of juice = 140
Question 6.
x varies inversely as twice of y. Given that when y = 6, the value of x is 4. Find the value of x when y = 8.
Solution:
Given x varies inversely as twice of y.
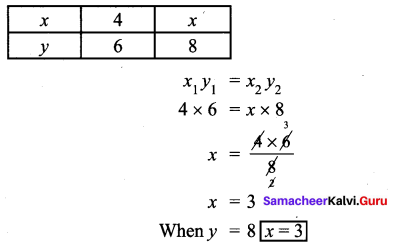
Question 7.
A truck requires 108 litres of diesel for covering a distance of 594 km. How much diesel will be required to cover a distance of 1650 km?
Solution:
Let the required distance be x

As the distance increases fuel quantity also increases.
∴ They are direct proportion.
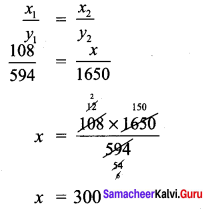
∴ The diesel required = 300 liters
Challenge Problems
Question 8.
If the cost of a dozen soaps is ₹ 396, what will be the cost of 35 such soaps?
Solution:
1 dozen = 12
Cost of 12 soaps = ₹ 396
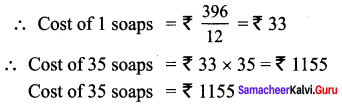
Question 9.
In a school there is 7 periods a day each of 45 minutes duration. How long each period is if the school has 9 periods a day assuming the number of hours to be the same?
Solution:
Number of periods increases as duration decreases, since the number of hours is same.
Let the duration of each period be x.

Question 10.
Cost of 105 note books is ₹ 2415. How many notebooks can be bought for ₹ 1863?
Solution:
For 2415 number of notebooks bought = 105

Question 11.
10 farmers can plough a field in 21 days. Find the number of days reduced if 14 farmers ploughed the same field?
Solution:
Let the required number of days if 14 farmers ploughed = x

As number of farmers increases, number of days decreases.
∴ They are in inverse proportion
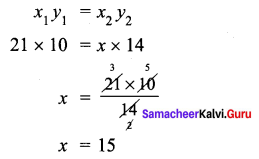
Initially the farmers worked for 21 days. Now they worked for 15 days.
∴ The number of days reduced = 21 – 15 = 6 days
Question 12.
A flood relief camp has food stock by which 80 people can be benefited for 60 days. After 10 days 20 more people have joined the camp. Calculate the number of days of food shortage due to the addition of 20 more people?
Solution:
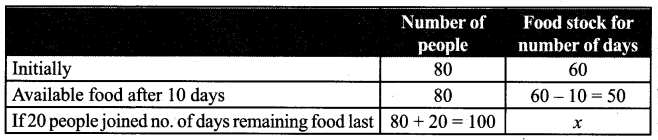
As number of people increases food last for less number of days.
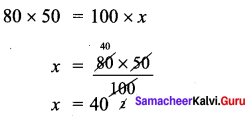
Remaining food is to be used for 50 days.
But it only last for 40 days.
No. of days shortage = 50 – 40 = 10 days.
∴ 10 days of food shortage due to the addition of 20 more people.
Question 13.
Six men can complete a work in 12 days. Two days later, 6 more men joined them. How many days will they take to complete the remaining work?
Solution:

As the number of men increases number of days increases.
∴ They are inversely proportional
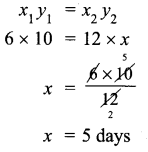
x = 5 days
∴ Remaining work will be complete in 5 days