Students can Download Maths Chapter 5 Geometry Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Additional Questions
Exercise 5.1
Question 1.
Can two adjacent angles be supplementary?
Solution:
Yes, In the figure
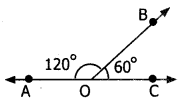
∠AOB and ∠BOC are adjacent angles.
Also ∠AOB + ∠BOC = 180°
∴ ∠AOB and ∠BOC are supplementary
Question 2.
Can two obtuse angles form a linear pair?
Solution:
No, the sum of the measures of two obtuse angles is more than 180°.
Question 3.
Can two right angles form a linear pair?
Solution:
Yes, because the sum of two right angles is 180° and form a linear pair.
![]()
Question 4.
Find x, y and z from the figure.
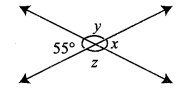
Solution:
x = 55° vertically opposite angles
y + 55° = 180°
y = 180°- 55°
y = 125°
Execise 5.2
Question 1.
Can two lines intersect in more than one point ?
Solution:
No, two lines cannot intersect in more than one point.
Question 2.
In the figure EF parallel to GH
Solution:
∠EAB = 60° and ∠ACD = 105°
Determine (i) ∠CAF and
(ii) ∠BAC
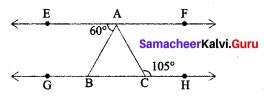
Solution:
(i) Since EF || GH and AC is a transversal
⇒ ∠CAF + ∠ACH = 180°
⇒ ∠CAF + 105° = 180° .
= 75°
(ii) ∴ EF || GH and AC is transversal.
∴ ∠EAC = ∠ACH [ ∵ Alternate interior angles]
⇒ ∠BAC = 105°
⇒ ∠BAC + ∠BAB = 105°
⇒ ∠BAC + 60° = 105°
⇒ ∠BAC = 105° – 60°
= 45°
∴ ∠CAF = 75° and ∠BAC = 45°.
![]()
Question 3.
In the given figure, the arms of two angles are parallel. If ∠ABC = 70°, then find
(i) ∠DGC
(ii) ∠DEF
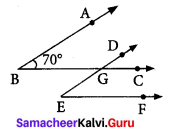
Solution:
We have AB||ED and BC || EF
(i) BC is transversal
∠DGC = ∠ABC [corresponding angles]
But ∠ABC = 70°
∠DGC = 70°
(ii) ED is a transversal to BC||EF
∴ ∠DEF = ∠DGC [corresponding]
∠DGC = 70°
∠DEF = 70°
Exercise 5.6
Question 1.
In the following figure, show that CD || EF
Solution:
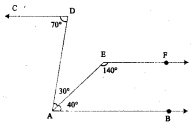
∠BAD = ∠BAE + ∠EAD
= 40°+ 30° = 70°.
and ∠CDA = 70°
∠BAD = ∠CDA
But they form a pair of alternate angles
⇒ AB || CD
Also ∠BAE + ∠AEF = 40° + 140° = 180°
But they form a pair of interior opposite angles.
⇒ AB || EF
From (1) and (2), we get
AB || CD || EF
⇒ CD || EF
![]()
Question 2.
In the adjoining figure, the lines \(\overleftrightarrow { AB } \) and \(\overleftrightarrow { CD } \) intersect at ‘O’. If ∠COB = 50°, find the measures of the other three angles.
Solution:
∠COB = 50°
∠AOD = 50° (vertically opposite angles)
Now ∠AOC and ∠COB form a linear pair,
Thus ∠AOC + ∠COB = 180°
⇒ ∠AOC + 50° = 180°.
∠AOC = 180° – 50° = 130°
Also ∠AOC and ∠BOD are vertically opposite angles.
∴ ∠BOD = ∠AOC = 130°
Thus the three angles are
∠AOD = 50°
∠AOC =130°
∠BOD = 130°