Students can Download Maths Chapter 5 Geometry Ex 5.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.3
Question 1.
Draw a line segment of given length and construct a perpendicular bisector to each line segment using scale and compass
(a) 8 cm
(b) 7 cm
(c) 5.6 cm
(d) 10.4 cm
(e) 58 cm
Solution:
(a) 8 cm
Construction :
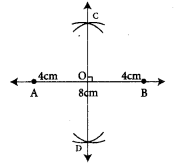
Step 1: Drawn a line. Marked two points A and B on it so that AB = 8 cm
Step 2: Using compass with A as centre and radius more than half of the length of AB, drawn two arcs of the same length one above AB and one below AB
Step 3: With the same radius and B as centre drawn two arcs to cut the arcs drawn in step 2. Marked the points of intersection of the arcs as C and D.
step 4: Joined C and D, CD intersect AB. Marked the point of intersection as ‘O’.
CD is the required perpendicular bisector of AB.
![]()
(b) 7 cm
Construction :
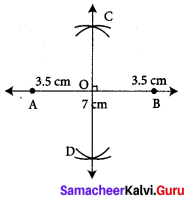
step 1: Drawn a line and marked points A and B on it so that AB = 7 cm.
step 2: Using compass with A as centre and radius more than half of the length of AB drawn two arcs of same length one above AB and one below AB.
step 3: With the same radius and B as centre drawn two arcs to cut the already drawn arcs in step 2. Marked the intersection of the arcs as C and D
step 4: Joined C and D, CD is the required perpendicular bisector of AB.
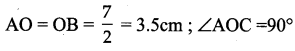
![]()
(c) 5.6 cm.
Construction :
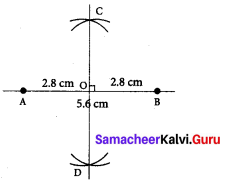
Step 1: Drawn a line and marked two points A and B on it so that AB = 5.6cm
Step 2: Using compass with A as centre and radius more than half of the length of AB, drawn two arcs of the same length, one above AB and one below AB
Step 3: With the same radius and B as centre drawn two arcs to cut the arcs drawn in step 2 and marked the points of intersection of the arcs as C and D
Step 4: Joined C and D. CD intersects AB. Marked the point of intersection as ‘O’CD is the required perpendicular bisector of AB.
Now ∠AOC = 90° AO = BO = 2.8 cm
![]()
(d) 10.4 cm
Construction :
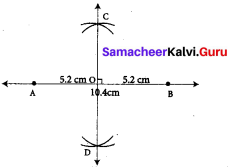
Step 1: Drawn a line and marked two points A and B on it so that AB = 10.4 cm.
Step 2: Using compass with A as centre and radius more than half of the length of AB, drawn two arcs of same length one above AB and one below AB.
Step 3: With the same radius and B as centre drawn two arcs to cut the arcs drawn in step 2 and marked the points of intersection of the arcs as C and D.
Step 4: Joined C and D. CD intersects AB. Marked the points of intersection as O. CD is the required perpendicular bisector.
Now ∠AOC = 90° ; AO = BO = 5.2 cm
![]()
(e) 58 mm
![]()
Construction :
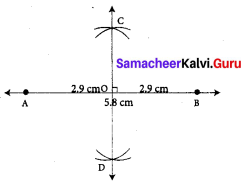
Step 1: Drawn a line. Marked two points A and B on it so that
AB = 5.8 cm = 58 mm.
Step 2: Using compass with A as centre and radius more than half of the length of AB, drawn two arcs of the same length one above AB and one below AB.
Step 3: With the same radius and B as centre drawn two arcs to cut the arcs of drawn in step 2. Marked the points of intersection of the arcs as C and D.
Step 4: Joined C and D. CD intersects AB. Marked the point of intersection as O. CD is the required perpendicular bisector. ∠AOC = 90°
AO = BO = 2.9 cm