Students can Download Maths Chapter 5 Geometry Ex 5.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.5
Question 1.
Construct the following angles using ruler and compass only.
(i) 60°
(ii) 120°
(iii) 30°
(iv) 90°
(v) 45°
(vi) 150°
(vii) 135°
Solution:
(i) 60°
Construction :
Step 1: Drawn a line and marked a point ‘A’ on it.
Step 2: With A as center drawn an arc of convenient radius to meet the line at a point B.
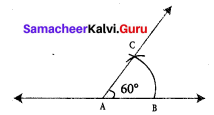
Step 3: With the same radius and B as center drawn an arc to cut the previous arc at C.
Step 4: Joined AC. The ∠ABC is the required angle with the measure 60°.
(ii) 120°
Construction :
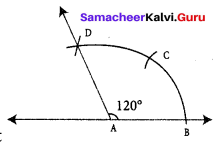
We know that there are two 60° angles in 120°.
∴ We can construct two 60° angles consecutively construct 120°
Step 1: Drawn a line and marked a point ‘A’ on it.
Step 2: With ‘A’ as center, drawn an arc of convenient radius to the line at a point B.
Step 3: With the same radius and B as center, drawn an arc to cut the previous arc at C.
Step 4: With the same radius and C as center, drawn an arc to cut the arc drawn in step 2 at D.
Step 5: Joined AD. Then ∠BAD is the required angle with measure 120°.
![]()
(iii) 30°
Constructions :
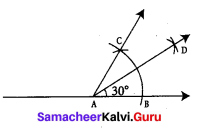
Since 30° is half of 60°, we can construct 30° by bisecting the angle 60°.
Step 1: Drawn a line and marked a point A on it.
Step 2: With A as center drawn an arc of convenient radius to the line to meet at a point B.
Step 3: With the same radius and B as center drawn an arc to cut the previous arc at C.
Step 4: Joined AC to get ∠BAC = 60°
Step 5: With B as center drawn an arc of convenient radius in the interior of ∠BAC
Step 6: With the same radius and C as center drawn an arc to cut the previous arc at D.
Step 7: Joined AD.
∴ ∠BAD is the required angle of measure 30°.
![]()
(iv) 90°
Construction :
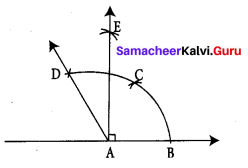
Step 1: Drawn a line and marked a point ‘A’ on it.
Step 2: With ‘A’ as center, drawn an arc of convenient radius to the line at a point B.
Step 3: With the same radius and B as center drawn an arc to cut the previous arc at ‘C’.
Step 4: With the same radius and C as center, drawn an arc to cut the arc drawn in step 2 at D.
Step 5: Joined AD. ∠BAD = 120°.
Step 6: With C as center, drawn an arc of convenient radius in the interior of ∠CAD.
Step 7: With the same radius and D as center, drawn an arc to cut the arc at E.
Step 8: Joined AF ∠BAE = 90°.
(v) 45°
Construction :
Step 1: Drawn a line and marked a point A on it
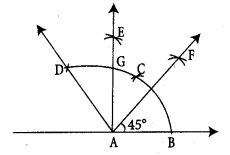
Step 2: With A as center, drawn an arc of convenient radius to the line at a point B.
Step 3: With the same radius and B as center drawn an arc to cut the previous arc at C.
Step 4: With the same radius and C as center, drawn an arc to cut the arc drawn in step 2 at D.
Step 5: Joined AD. ∠BAD = 120°.
Step 6: With G as center and any convenient radius drawn an arc in the interior of ∠GAB
Step 7: With the same radius and B as center drawn an arc to cut the arc at F.
Step 8: Joined AF. ∠BAF = 45°
![]()
(vi) 150°
Construction :
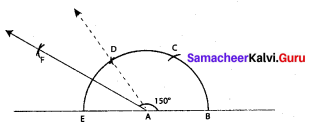
Since 150° = 60° + 60° + 30°; we construct as follows
Step 1: Drawn a line and marked a point A on it.
Step 2: With ‘A’ as center, drawn a full arc of convenient radius to the line at a point B and at E the other end.
Step 3: With the same radius and B as center, drawn an arc to cut the previous arc at C.
Step 4: With the same radius and C as center drawn an arc to cut the already drawn arc at D.
Step 5: With D as center, drawn an arc of convenient radius in the interior of ∠DAE
Step 6: With E as center and with the same radius drawn an arc to cut the previous arc at F.
Step 7: Joined AF, ∠FAB = 150°.
(vii) 135°
Construction :
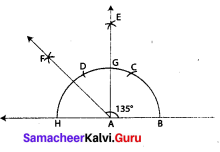
Step 1: Drawn a line and marked a point A on it.
Step 2: With ‘A’ as center, drawn an arc of convenient radius to the line at a point B.
Step 3: With the same radius and B as center drawn an arc to cut the previous arc at C.
Step 4: With the same radius and C as center, drawn an arc to cut the arc at D.
Step 5: With C and D as centers drawn arcs of convenient (same) radius in the interior of ∠CAD. Marked the point of intersection as E.
Step 6: Joined AE, through G. ∠BAE = 90°.
Step 7: Drawn angle bisector to ∠GAH through F.
Now ∠BAF = 135°.