Students can Download Maths Chapter 1 Number System Ex 1.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 1 Number System Ex 1.5
Question 1.
Write the following decimal numbers in the place value table.
(i) 247.36
(ii) 132.105
Solution:
(i) 247.36

(ii) 132.105

Question 2.
Write each of the following as decimal number.
(i) 300 + 5 + \(\frac { 7 }{ 10 } \) + \(\frac { 9 }{ 100 } \) + \(\frac { 2 }{ 100 } \)
(ii) 1000 + 400 + 30 + 2 + \(\frac { 6 }{ 10 } \) + \(\frac { 7 }{ 100 } \)
Solution:
(i) 300 + 5 + \(\frac { 7 }{ 10 } \) + \(\frac { 9 }{ 100 } \) + \(\frac { 2 }{ 100 } \) = 305.792
(ii) 1000 + 400 + 30 + 2 + \(\frac { 6 }{ 10 } \) + \(\frac { 7 }{ 100 } \) = 1432.67
![]()
Question 3.
Which is greater?
(i) 0.888 (or) 0.28
(ii) 23.914 (or) 23.915
Solution:
(i) 0.888 (or) 0.28
The whole number parts is equal for both the numbers.
Comparing the digits in the tenths place we get, 8 > 2.
0.888 > 0.28 ∴ 0.888 is greater.
(ii) 23.914 or 23.915
The whole number part is equal in both the numbers.
Also the tenth place and hundredths place are also equal.
∴ Comparing the thousandths place, we get 5 > 4.
23.915 > 23.914 ∴ 23.915 is greater.
Question 4.
In a 25 m swimming competition, the time taken by 5 swimmers A, B, C, D and E are 15.7 seconds, 15.68 seconds, 15.6 seconds, 15.74 seconds and 15.67 seconds respectively. Identify the winner.
Solution:
The winner is one who took less time for swimming 25 m.
Comparing the time taken by A, B, C, D, E the whole number part is equal for all participants.
Comparing digit in tenths place we get 6 < 7.
∴ Comparing 15.68, 15.6, 15.67, that is comparing the digits in hundredths place we get 15.60 < 15.67 < 15.68
One who took 15.6 seconds is the winner. ∴ C is the winner.
![]()
Question 5.
Convert the following decimal numbers into fractions
(i) 23.4
(ii) 46.301
Solution:
(i) 23.4 = \(\frac { 234 }{ 10 } \) = \(\frac{234 \div 2}{10 \div 2}\) = \(\frac { 117 }{ 5 } \)
(ii) 46.301 = \(\frac { 46301 }{ 1000 } \)
Question 6.
Express the following in kilometres using decimals,
(i) 256 m
(ii) 4567 m
Solution:
1 m = \(\frac { 1 }{ 1000 } \) km = 0.001 Km
(i) 256 m = \(\frac { 256 }{ 1000 } \) km = 0.256 km
(ii) 4567 m = \(\frac { 4567 }{ 1000 } \) km = 4.567 km
Question 7.
There are 26 boys and 24 girls in a class. Express the fractions of boys and girls as decimal numbers.
Solution:
Boys = 26; Girls = 24; Total = 50
Fraction of boys = \(\frac { 26 }{ 50 } \) = \(\frac{26 \times 2}{50 \times 2}\) = \(\frac { 52 }{ 100 } \) = 0.52
Fraction of girls = \(\frac { 24 }{ 50 } \) = \(\frac{24 \times 2}{50 \times 2}\) = \(\frac { 48 }{ 100 } \) = 0.48
Challenge Problems
Question 8.
Write the following amount using decimals.
(i) 809 rupees 99 paise
(ii) 147 rupees 70 paise
Solution:
100 paise = 1 rupee; 1 paise = \(\frac { 1 }{ 100 } \) rupee
(i) 809 rupees 99 paise = 809 rupees + \(\frac { 99 }{ 100 } \) rupees
= 809 + 0.99 rupees = ₹ 809.99
(ii) 147 rupees 70 paise = 147 rupees + \(\frac { 70 }{ 100 } \) rupees
= 147 rupees + 0.70 rupees = ₹ 147.70
Question 9.
Express the following in metres using decimals.
(i) 1328 cm
(ii) 419 cm
Solution:
100 cm = 1 m; 1 cm = \(\frac { 1 }{ 100 } \) m
(i) 1328 cm = \(\frac { 1328 }{ 100 } \) m = 13.28 m
(ii) 419 cm = \(\frac { 419 }{ 100 } \) m = 4.19 m
![]()
Question 10.
Express the following using decimal notation.
(i) 8 m 30 cm in metres
(ii) 24 km 200 m in kilometres
Solution:
(i) 8 m 30 cm in metres
8 m + \(\frac { 30 }{ 100 } \) m = 8 m + 0.30 m = 8.30 m
(ii) 24 km 200 m in kilometres
24 km + \(\frac { 200 }{ 1000 } \) km = 24 km + 0.200 km = 24.200 km
Question 11.
Write the following fractions as decimal numbers.
(i) \(\frac { 23 }{ 10000 } \)
(ii) \(\frac { 421 }{ 100 } \)
(iii) \(\frac { 37 }{ 10 } \)
Solution:
(i) \(\frac { 23 }{ 10000 } \) = 0.0023
(ii) \(\frac { 421 }{ 100 } \) = 4.21
(iii) \(\frac { 37 }{ 10 } \) = 3.7
Question 12.
Convert the following decimals into fractions and reduce them to the lowest form,
(i) 2.125
(ii) 0.0005
Solution:
(i) 2.125 = \(\frac { 2125 }{ 1000 } \) = \(\frac{2125 \div 25}{1000 \div 25}\) = \(\frac { 85 }{ 40 } \) = \(\frac{85 \div 5}{40 \div 5}\) = \(\frac { 17 }{ 8 } \)
(ii) 0.0005 = \(\frac { 5 }{ 1000 } \) = \(\frac{5 \div 5}{10000 \div 5}\) = \(\frac { 1 }{ 2000 } \)
Question 13.
Represent the decimal numbers 0.07 and 0.7 on a number line.
Solution:
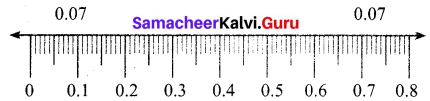
0.07 lies between 0.0 and 0.1
The unit space between 0 and 0.1 is divided into 10 equal parts and 7th part is taken. Also 0.7 lies between 0 and 1.
The unit space between 0 and 1 is divided into 10 equal parts, and the 7th part is taken.
![]()
Question 14.
Write the following decimal numbers in words.
(i) 4.9
(ii) 220.0
(iii) 0.7
(iv) 86.3
Solution:
(i) 4.9 = Four and nine tenths
(ii) 220.0 = Two hundred and twenty
(iii) 0.7 = Seven tenths
(iv) 86.3 = Eighty six and three tenths.
Question 15.
Between which two whole numbers the given numbers lie?
(i) 0.2
(ii) 3.4
(iii) 3.9
(iv) 2.7
(v) 1.7
(vi) 1.3
Solution:
(i) 0.2 lies between 0 and 1.
(ii) 3.4 lies between 3 and 4.
(iii) 3.9 lies between 3 and 4.
(iv) 2.7 lies between 2 and 3.
(v) 1.7 lies between 1 and 2.
(vi) 1.3 lies between 1 and 2.
![]()
Question 16.
By how much is \(\frac { 9 }{ 10 } \) km less than 1 km. Express the same in decimal form.
Solution:
Given measures are 1 km and \(\frac { 9 }{ 10 } \) km. i.e., 1 km and 0.9 km.
Difference = 1.0 – 0.9 = 0.1 km.