Students can Download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Ex 3.4
Miscellaneous Practice Problems
Question 1.
62 × 6m = 65, find the value of ‘m’
Solution:
62 × 6m = 65
62+m = 65 [Since am × an= am+n]
Equating the powers, we get
2 + m = 5
m = 5 – 2 = 3
Question 2.
Find the unit digit of 124128 × 126124
Solution:
In 124128, the unit digit of base 124 is 4 and the power is 128 (even power).
Therefore, unit digit of 124128 is 4.
Also in 126124, the unit digit of base 126 is 6 and the. power is 124 (even power).
Therefore, unit digit of 126124 is 6.
Product of the unit digits = 6 × 6 = 36
∴ Unit digit of the 124128 × 126124 is 6.
Question 3.
Find the unit digit of the numeric expression: 1623 + 7148 + 5961
Solution:
In 1623, the unit digit of base 16 is 6 and the power is 23 (odd power).
Therefore, unit digit of 1623 is 6.
In 7148, the unit digit of base 71 is 1 and the power is 48 (even power).
Therefore, unit digit of 7148 is 1.
Also in 5961, the unit digit of base 59 is 9 and the power is 61 (odd power).
Therefore, unit digit of 5961 is 9.
Sum of the unit digits = 6 + 1 + 9 = 16
∴ Unit digit of the given expression is 6.
![]()
Question 4.
Find the value of
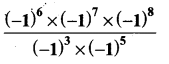
Solution:
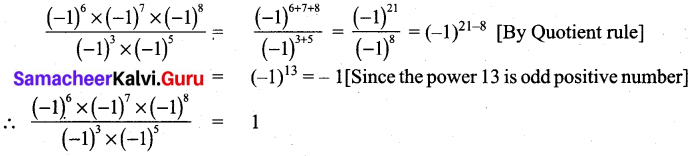
Question 5.
Identify the degree of the expression, 2a3be + 3a3b + 3a3c – 2a2b2c2
Solution:
The terms of the given expression are 2a3bc, 3a3b + 3a3c – 2a2b2c2
Degree of each of the terms: 5,4,4,6.
Terms with the highest degree: – 2a2b2c2
Therefore degree of the expression is 6.
Question 6.
If p = -2, q = 1 and r = 3, find the value of 3p2q2r.
Solution:
Given p = -2; q = 1; r = 3
∴ 3p2q2r = 3 × (-2)2 × (1)2 × (3)
= 3 × (-2 × 1)2 × (3) [Since am × bm = (a × b)m]
= 3 × (-2)2 × (3)
= 3 × (-1)2 × 22 × 3
= 31+1 × 1 × 4 [Since am × an = am+n]
= 32 × 4 = 9 × 4
∴ 3p2q2r = 36
![]()
Challenge Problems
Question 7.
LEADERS is a WhatsApp group with 256 members. Every one of its member is an admin for their own WhatsApp group with 256 distinct members. When a message is posted in LEADERS and everybody forwards the same to their own group, then how many members in total will receive that message?
Solution:
Members of the groups LEADERS = 256
Members is individual groups of the members of LEADERS = 256
Total members who receive the message

= 256 × 256 = 28 × 28
28+8 = 216
= 65536
Totally 65536 members receive the message.
![]()
Question 8.
Find x such that 3x+2 = 3x + 216.
Solution:
Given 3x+2 = 3x + 216 ; 3x+2 = 3x + 216
Dividing throught by 3x, we get

Equating the powers of same base
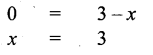
Question 9.
If X = 5x2 + 7x + 8 and Y = 4x2 – 7x + 3, then find the degree of X + Y.
Solution:
Given x = 5x2 + 7x + 8
X + Y = 5x2 + 7x + 8 + (4x2 – 7x + 3)
= (5x2 + 4x2) + (7x – 7x) + (8 + 3)
= x2 (5 + 4) + x(7 – 7) + (8 + 3) = 9x2 + 11
Degree of the expression is 2.
Question 10.
Find the degree of (2a2 + 3ab – b2) – (3a2 -ab- 3b2)
Solution:
(2a2 + 3ab – b2) – (3a2 – ab – 3b2)
= (2a2 + 3ab – b2) + (- 3a2 + ab + 3b2)
= 2a2 + 3ab – b2 – 3a2 + ab + 3b2
= 2a2 – 3a2 + 3ab + ab + 3b2 – b2
= 2a2 – 3a2 + ab (3 + 1) + b2(3 – 1)
= – a2 + 4 ab + 2b2
Hence degree of the expression is 2.
![]()
Question 11.
Find the value of w, given that x = 4, y = 4, z = – 2 and w = x2 – y2 + z2 – xyz.
Solution:
Given x = 3; y = 4 and z = -2.
w = x2 – y2 + z2 – xyz
w = 32 – 42 + (-2)2 – (3)(3)(-2)
w = 9 – 16 + 4 + 24
w = 37 – 16
w = 21
Question 12.
Simplify and find the degree of 6x2 + 1 – [8x – {3x2 – 7 – (4x2 – 2x + 5x + 9)}]
Solution:
6x2 + 1 – [8x – (3x2 – 7 – (4x2 – 2x + 5x + 9)}]
= 6x2 + 1 – [8x – {3x2 – 7 – 4x2 – 2x + 5x + 9}]
= 6x2 + 1 – [8x – 3x2 + 7 + 4x2 – 2x + 5x + 9}]
= 6x2 – 1 – [8x + 3x2 – 7 – 4x2 + 2x – 5x – 9]
= 6x2 + 3x2 – 4x2 – 8x + 2x – 5x – 1 – 7 – 9]
= x2(6 + 3 – 4) + x(8 + 2 – 5) – 15
= 5x2 – 11x – 15
Degree of the expression is 2.
![]()
Question 13.
The two adjacent sides of a rectangle are 2x2 – 5xy + 3z2 and 4xy – x2 – z2. Find the perimeter and the degree of the expression.
Solution:
Let the two adjacent sides of the rectangle as
l = 2x2 – 5xy + 3z2 and b = 4xy – x2y + 3z2
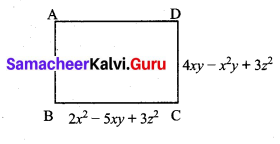
Perimeter of the rectangle
= 2(l + b) = 2(2x2 – 5xy + 3z2 + 4xy – x2 – z2)
= 4x2 – 10xy + 6z2 + 8xy – 2x2 – 2z2
= 4x2 – 2x2 – 10xy + 8xy + 6z2 – 2z2
= x2(4 – 2) + xy (-10 + 8) + z2 (6 – 2z2)
Perimeter = 2x2 – 2xy + 4z2
Degree of the expression is 2.