Students can Download Maths Chapter 4 Geometry Ex 4.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.3
Miscellaneous Practice Problems
Question 1.
In an isoscales triangle one angle is 76°. If the other two angles are equal, find them.
Solution:
In an isoscales triangle, angle opposite to equal sides are equal. Let the equal angles be x° and x°.
In a triangle the sum of the three angles is 180°.
x° + x° + 76° = 180°
x° (1 + 1) = 180° – 76° = 104°
2x = 104°
x = \(\frac{104^{\circ}}{2}\) = 52°
x = 52°
∴ Other two angles are 52° and 52°.
Question 2.
If two angles of a triangle are 46° each, how can you classify the triangle?
Solution:
Given two angles of the triangle are same and is equal to 46°. If two angles are equal the sides opposite to equal angles are equal. Therefore it will be an isoscales triangle.
![]()
Question 3.
If an angle of a triangle is equal to the sum of the other two angles, find the type of the triangle.
Solution:
Let ∠B is the greater angle then by the given condition ∠B = ∠A + ∠C.
Sum of three angle of a triangle = 180°.
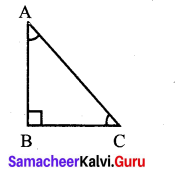
∠A + ∠B + ∠C = 180°.
∠A + (∠A + ∠C) + ∠C) = 180°.
2∠A + 2∠C = 180°
2(∠A + ∠C) = 180°
∠A + ∠C = \(\frac{180^{\circ}}{2}\)
∠B = 90°
∴ One of the angle of the triangle = 90°
It will be a right angled triangle.
Question 4.
If the exterior angle of a triangle is 140° and its interior opposite angles are equal, find all the interior angles of the triangle.
Solution:
Given the exterior angle = 140°
Interior opposite angle are equal.
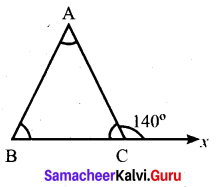
Let one of the interior opposite angle be x.
Then x + x = 140°.
[∵ Exterior angle = sum of interior opposite angles]
2x = 140°
x = \(\frac{140^{\circ}}{2}\) = 70°
x = 70°
Interior opposite angle = 70°, 70°.
Sum of the three angles of a triangle = 180°.
70° + 70° + Third angle = 180°
140° + Third angle = 180°
Third angle = 180° – 140° = 40°
∴ Interior angle are 40°, 70°, 70°.
![]()
Question 5.
In ∆JKL, if ∠J = 60° and ∠K = 40°, then find the value of exterior angle formed by extending the side KL.
Solution:
When extending the side KL, the exterior angle formed in equal
to the sum of the interior opposite angles.
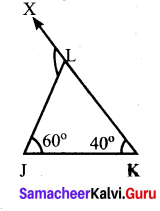
∠JLX = ∠LJK + ∠LKJ
= 60°+ 40° =100°
Exterior angle formed = 100°
Question 6.
Find the value of ‘x’ in the given figure.
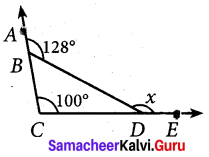
Solution:
Given ∠DCB = 1000 and ∠DBA = 128°
In the given figure
∠CBD + ∠DBA = 180°
∠CBD + 128° = 180°
∠CBD = 52°
Now exterior angle x = Sum of interior opposite angles.
x = ∠DCB + ∠CBD = 100° + 52° = 152°
x = 152°
![]()
Question 7.
If ∆MNO ≅ ∆DEF, ∠M = 60° and ∠E = 45° then find the value of ∠O.
Solution:
Given ∆MNO ≅ ∆DEF
∴ Corresponding parts of conqruent triangle are congruent.
∠M = ∠D = 60° [given ∠M = 60°]
∠N = ∠E = 45° [given ∠E = 45°]
∠O = ∠F
In triangle MNO, sum of the three angle – 180°.
∠M + ∠N + ∠O = 180°
60° + 45° + ∠O = 180°
105° + ∠O = 180°
∠O = 180° – 105° = 75°
Value of ∠O = 75°
Question 8.
In the given figure ray AZ bisects ∠BAD and ∠DCB, prove that
(i) ∆BAC ≅ ∆DAC
(ii) AB = AD
Solution:
(i) In ∆BAC and ∆DAC
∠BAC = ∠DAC [Given \(\overline{A Z}\) bisects ∠BAD]
∠BCA = ∠DCA[\(\overline{A Z}\) bisects ∠DCB]
AC = AC [∵ common side]
∴ Here AC is the included side of the angles. By ASA criterior, ∆BAC ≅ ∆DAC.
(ii) By (i) ∆BAC ≅ ∆DAC
BA = DA [By CPCTC]
i.e., AB = AD
![]()
Question 9.
In the given figure FG = FI and H is midpoint of GI, prove that ∆FGH ≅ ∆FHI
Solution:
In ∆FGH and ∆FHI
Given FG = HI
Also, GH = HI [∵ H is the midpoint of GI]
FH = FH [Common]
∴ By S.SS congruency criteria, ∆FGH ≅ ∆FIH. Hence proved.
Question 10.
Using the given figure, prove that the triangles are congruent. Can you conclude that AC is parallel to DE.
Solution:
In ∆ABC and ∆EBD,
AB = EB
BC = BD
∠ABC = ∠EBD [∵ Vertically opposite angles]
By SAS congruency criteria. ∆ABC ≅ ∆EBD.
We know that corresponding parts of congruent triangles are congruent.
∴ ∠BCA ≅ ∠BDE
and ∠BAC ≅ ∠BED
∠BCA ≅ ∠BDE means that alternate interior angles are equal if CD is the transversal to lines AC and DE.
Similarly, if AE is the transversal to AC and DE, we have ∠BAC ≅ ∠BED
Again interior opposite angles are equal.
We can conclude that AC is parallel to DE.
![]()
Challenge Problems
Question 11.
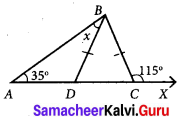
In given figure BD = BC, find the value of x.
Solution:
Given that BD = BC
∆BDC is on isoscales triangle.
In isoscales triangle, angles opposite to equal sides are equal.
∠BDC = ∠BCD ……(1)
Also ∠BCD + ∠BCX = 180° [∵ Liner Pair]
∠BCD + 115° = 180°
∠BCD = 180° – 115°
∠BCD = 65° [By (1)]
In ∆ADB
∠BAD + ∠ADB = ∠BDC
[∵ BDC is the exterior angle and ∠BAD and ∠ABD are interior opposite angles]
35° + x = 65°
x = 65° – 35°
x = 30°
Question 12.
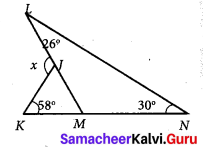
In the given figure find the value of x.
Solution:
For ∆LNM, ∠LMK is the exterior angle at M.
Exterior angle = sum of opposite interior angles
∠LMK = ∠MLN + ∠LNM = 26° + 30° = 56°
∠JMK = 56° [∵ ∠LMK = ∠JMK]
x is the exterior angle at J for ∆JKM.
∴ x = ∠JKM + ∠KMJ [∵ Sum of interior opposite angles]
x = 58° + 56° [∵ ∠JMK = 56°]
x = 114°
Question 13.
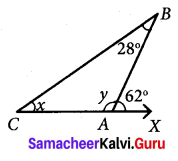
In the given figure find the values of x and y.
Solution:
In ∆BCA, ∠BAX = 62° is the exterior angle at A.
Exterior angle = sum of interior opposite angles.
∠ABC + ∠ACB = ∠BAX
28°+ x = 62°
x = 62° – 28° = 34°
Also ∠BAC + ∠BAX = 180° [∵ Linear pair]
y + 62° = 180°
y = 180° – 62° = 118°
x = 34°
y = 118°
![]()
Question 14.
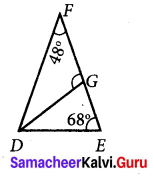
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD.
Solution:
Given ∠F = 48°
∠E = 68°
In ∆DEF,
∠D + ∠F + ∠E = 180° [By angle sum property]
∠D + 68° + 68° = 180°
∠D + 116° = 180°
∠D = 180° – 116° = 64°
Since DG is the angular bisector of ∠D.
∠FDG = ∠GDE
Also ∠FDG + ∠GDE = ∠D
2 ∠FDG = 64°
2 ∠FDG = 64°
∠FDG = \(\frac{64^{\circ}}{2}\) = 32°
∠FDG = 32°
In ∆FDG,
∠FDG + ∠GFD = 180° [By angle sum property of triangles]
32° + ∠FDG + 48° = 180°
∠FDG + 80° = 180°
∠FDG = 180° – 80°
∠FDG = 100°
![]()
Question 15.
In the figure find the value of x.
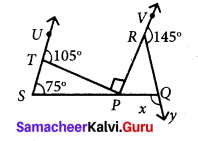
Solution:
Exterior angle is equal to the sum of opposite interior angles.
in ∆TSP ∠TSP + ∠SPT = ∠UTP
75° + ∠SPT = 105°
∠SPT = 105° – 75°
∠SPT = 30° ……(1)
∠SPT + ∠TPR + ∠RPQ = 180° [∵ Sum of angles at a point on a line is 180°]
30° + 90° + ∠RPQ = 180°
120° + ∠RPQ = 180°
∠RPQ = 180° – 120°
∠RPQ = 60° …… (2)
∠VRQ + ∠QRP = 180° [∵ linear pair]
145° + ∠QRP = 180°
∠QRP = 180° – 145°
∠QRP = 35°
Now in ∆ PQR
∠QRP + ∠RPQ = x [∵ x in the exterior angle]
35° + 60° = x
95° = x
![]()
Question 16.
From the given figure find the value of y.
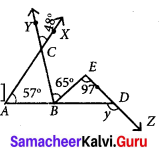
Solution:
From the figure,
∠ACB = ∠XCY [Vertically opposite angles]
∠ACB = 48° …(1)
In ∆ABC, ∠CBD is the exterior angle at B.
Exterior angle = Sum of interior opposite angles.
∠CBD = ∠BAC + ∠ACB
∠CBE + ∠EBD = 57° + 48°
65° + ∠EBD = 105°
∠EBD = 105° + 65° = 40° ……… (2)
In ∆EBD, y is the exterior angle at D.
y = ∠EBD + ∠BED
[∵ Exterior angle = Sum of opposite interior angles]
y = 40° + 97° [∵ From (2)]
y = 137°