Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 1 Life Mathematics Ex 1.2

Students can Download Maths Chapter 1 Life Mathematics Ex 1.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 1 Life Mathematics Ex 1.2

Question 1.
Fill in the blanks:

Question (i)
Loss or gain percent is always calculated on the ………
Answer:
Cost price

Question (ii)
A mobile phone is sold for ? 8400 at a gain of 20%. The cost price of the mobile phone is …………
Answer:
₹ 7000
Hint:
Let cost price of mobile be ₹ x. Given that selling price is ? 8400 and gain is 20%

Question (iii)
An article is sold for ₹ 555 at a loss of 7\(\frac{1}{2}\)% the cost price qfthe article is ……….
Answer:
₹ 600
Hint:
Given selling price is ₹ 555 & loss is 7\(\frac{1}{2}\)%
as per formula,

Question (iv)
The marked price of a mixer grinder is ₹ 4500 is sold for ₹ 4140 after discount. The rate of discount is ……..
Answer:
8%
Hint:
Marked price is X 4500. Discounted price in ₹ 4140
∴ Discount = Marked price – Discounted price = 4500 – 4140 – 360

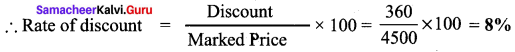
Question (v)
The total bill amount of a shirt costing ₹ 575 and a T-shirt costing ₹ 325 with GST of 5% is ………..
Answer:
₹ 945
Hint:
Cost price of shirt = ₹ 575 (CP)
GST = 5%

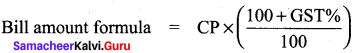
= 575 x (\(\frac { (100+5) }{ 100 } \)) = 575 x \(\frac { 105 }{ 100 } \)
= ₹ 603.75
Cost price of T-shirt = ₹ 325 (CP)
GST = 5%

= 325 x (\(\frac { (100+5) }{ 100 } \))
Total bill amount = ₹ 603.75 + ₹ 341.25 = ₹ 945

Question 2.
If selling an article for ₹ 820 causes 10% loss on the selling price, find its cost price.
Solution:
Given that selling price (SP) = ₹ 820
Loss % = 10 %

Question 3.
If the profit earned on selling an article for ₹ 810 is the same as loss on selling it for ₹ 530, then find the cost price of the article.
Solution:
Case 1: Profit = Selling price (SP) – Cost price (CP)
Case 2: Loss = Cost price (CP) – Selling price (SP)
Given that profit of case 1 = loss of case 2
∴ P = 810 – CP
L = CP – 530
Since profit (P) = loss (L)
810 – CP = CP – 530
∴ 2CP = 810 + 530 = 1340 ⇒ C.P = \(\frac{1340}{2}\)
∴ CP = 670

Question 4.
Some articles are bought at 2 for ₹ 15 and sold at 3 for ₹ 25. Find the gain percentage.
Solution:
Let cost price of one article be C.P
Given that 2 are bought for ₹ 15
∴ 2 x CP = 15 ⇒ CP = \(\frac{15}{2}\)
Let selling price of one article be SP
Given that 3 are sold for ₹ 25
∴ 3 x CP = 25 ⇒ SP = \(\frac{25}{3}\)
∴ Gain = SP – CP = \(\frac{25}{3}\) – \(\frac{15}{2}\) = \(\frac{50-45}{6}\) = \(\frac{5}{6}\)

Question 5.
If the selling price of 10 rulers is the same as the cost price of 15 rulers, then find the gain percentage.
Solution:
Let cost price of one ruler be x
Given that selling price (SP) of 10 rulers
i.e., same as cost price (CP) of 15 rulers
∴ SP of 10 rulers = 15 × x = 15x
SP of 1 ruler = \(\frac{15x}{10}\) = 1.5x
∴ Gain = SP of 1 ruler – CP of ruler = 1.5x -x = 0.5x

Question 6.
By selling a speaker for ₹ 768, a man loses 20%. In order to gain 20% how much should he sell the speaker?

Solution:
Selling price (SP) of speaker = ₹ 768
Loss % = 20%
as per formula

For gain of 20%, we should now calculate the selling price

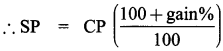
= 960 (\(\frac{100+20}{100}\)) = 960 x \(\frac{120}{100}\)
= 96 x 12 = ₹ 1152

Question 7.
A man sold two gas stoves for ₹ 8400 each. He sold one at a gain of 20% and the other at a loss of 20%. Find his gain or loss % in the whole transaction.

Solution:
Let the CP of gas stove 1 be x and gas stove 2 be y
Given that selling price (SP) for both is the same = ₹ 8400
Case i:
First gastove: Cost price (CP) = x
Selling Price (SP) = ₹ 8400
Gain % = 20%

Cost price of first gas stove = ₹ 7000

Case 2:
Second gastove: Cost price (CP) = y
Selling price (SP) = ₹ 8400
loss % = 20%

∴ Cost price of second stove = ₹ 10,500
From (1) and (2),
Total cost price = Cost of stove 1 + Cost of stove 2
= 7000+ 10500 = 17,500
Total selling price = SP of stove 1 + SP of stove 2
= 8400 + 8400 = 16,800
Now, we find that total selling price is less than total cost price, therefore it is a loss
∴ Loss = CP – SP= 17,500 – 16,800 = 700
Loss % = \(\frac{loss}{CP}\) x 100 = \(\frac{700}{17500}\) x 100 = 4%
Loss % = 4 %

Question 8.
Find the unknowns x, y and z

Solution:
(i) Book marked price = ₹ 225 discount = 8%

∴ 225 x (\(\frac { (100-8) }{ 100 } \))
= 225 x (\(\frac { 92 }{ 100 } \)) = ₹ 207

(ii) LED TV selling price = 11970 discount = 5%,

∴ 11970 = y x \(\frac { (100-d%) }{ 100 } \)
∴ y = \(\frac { 11970×100 }{ 95 } \) = 126 x 100 = ₹ 12,600

(iii) Digital clock marked price (MP) = ₹ 750, MP = ₹ 12,600
Selling price (SP) = ₹ 615, Discount = z

∴ 615 = 750 x \(\frac { (100-z) }{ 100 } \)
∴ (100 – z) = \(\frac { 615×100 }{ 700 } \)
100 – z = 82
∴ z = 100 – 82
Discouont = 18%

Question 9.
Find the total bill amount for the data below.

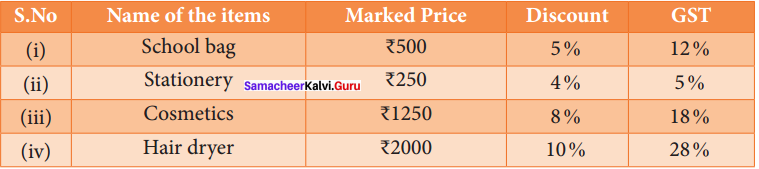
Solution:

For bill amount, we should apply GST on the discounted value of the items.

Total bill amount = Bill amount of School bag + Stationary + Cosmetics + Hair drier
= 532 + 252 + 1357 + 2304
= ₹ 4,445

Question 10.
A shopkeeper buys goods at \(\frac { 4 }{ 5 } \) of its marked price and sells them at \(\frac { 4 }{ 5 } \) of the marked price find his profit percentage.
Solution:
Let marked price be MP
Given that he buys good at \(\frac { 4 }{ 5 } \) of marked price
∴ CP (cost price) = \(\frac { 4 }{ 5 } \) MP
Given that selling price (SP) = \(\frac { 7 }{ 5 } \) x MP
∴ Profit = Selling price – Cost price = \(\frac { 7 }{ 5 } \) MP – \(\frac { 4 }{ 5 } \) MP = \(\frac { 3 }{ 5 } \)  MP

Question 11.
A branded AC has a marked price of ₹ 37250. There are 2 options given for the customer.

1. Selling Price is ₹ 37250 along with attractive gifts worth ₹ 3000 (or)
2. Discount of 8% but no free gifts. Which offer is better?

Marked price of AC = ₹ 37,250
Option 1:
Selling price = ₹ 37250 & gifts worth ₹ 3000
∴ Net gain for customer = ₹ 3000 as there is no discount on AC

Option 2:
Discount of 8%, but no gift

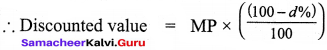
= 37250 x \(\frac { (100-8) }{ 100 } \) = 37250 x 0.92 = 34270
∴ Savings for customer = 37250 – 34270 = ₹ 2980
Therefore, the customer gets 3000 gift in option 1 where as he is able to save only ₹ 2980 in option 2. Therefore, option 1 is better.

Question 12.
If a mattress is marked for ₹ 7500 and is available at two successive discount of 10% and 20%, find the amount to be paid by the customer.
Solution:
Marked price of mattress = ₹ 7500
Discount d₁ = 10%
Discount d₂ = 20%

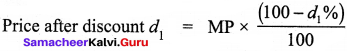
= 7500 x \(\frac { (100-10) }{ 100 } \) = 7500 x \(\frac { 90 }{ 100 } \) = 6750

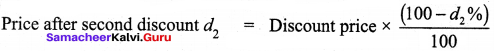
= 6750 x \(\frac { (100-20) }{ 100 } \) = ₹ 5400

Objective Type Questions

Question 13.
A fruit vendor sells fruits for ₹ 200 gaining ₹ 40. His gain percentage is –
(a) 20%
(b) 22%
(c) 25%
(d) 16\(\frac { 2 }{ 3 } \)
Answer:
(c) 25%
Hint:
Selling price = ₹ 200
Gain = 40
∴ CP = Selling price – gain = 200 – 40 = 160
Gain % = \(\frac { Gain }{ CP } \) x 100 = \(\frac { 40 }{ 160 } \) x 100 = 25%

Question 14.
By selling a flower pot for ₹ 528, a woman gains 20%. At what price should she sell it to gain 25%?
(a) ₹ 500
(b) ₹ 550
(c) ₹ 553
(d) ₹ 573
Answer:
(b) ₹ 550
Hint:
If selling price (SP) = ₹ 528
Gain % = 20%
∴ CP = ?

∴ 528 = CP x \(\frac { 100+20 }{ 100 } \)
∴ CP = \(\frac { 528×100 }{ 120 } \)
If gain % = 25 %, Selling ?

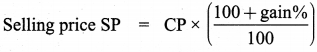
= 440 x \(\frac { (100+gain%) }{ 100 } \) = 440 x \(\frac { 125 }{ 100 } \)
= ₹ 550

Question 15.
A man buys an article for ₹ 150 and makes overhead expenses which are 12% of the cost price. At what price must he sell it to gain 5%?
(a) ₹ 180
(b) ₹ 168
(c) ₹ 176.40
(d) ₹ 85
Answer:
(c) ₹ 176.40
Hint:
Cost price of article = ₹ 150
Over head expenses = 12% of cost price = \(\frac { 12 }{ 100 } \) x 150 = ₹ 85
∴ Effective cost of article = 150 + 18 = ₹ 168
Now, to gain 5%, he has to sell at

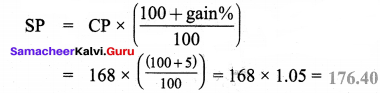
Question 16.
The price of a hat is ₹ 210. What was the marked price of the hat if it is bought at 16% discount?
(a) ₹ 243
(b) ₹ 176
(c) ₹ 230
(d) ₹ 250
Answer:
(d) ₹ 250
Hint:
Let marked price be MP
Discounted price = ₹ 210
Rate of discount = 16%
As per formula:

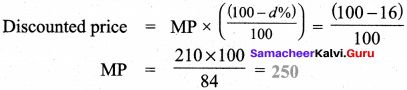
Question 17.
The single discount which is equivalent to two successive discount of 20% and 25% is –
(a) 40%
(b) 45%
(c) 5%
(d) 22.5%
Answer:
(a) 40%
Let marked price be MP, after discount 1 of 20%,

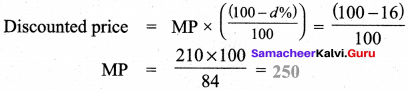
After discount 2 of 25%,

Comparing with formula, we get
∴ This is equivalent to a single discount of 40%