Students can Download Maths Chapter 1 Life Mathematics Ex 1.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 1 Life Mathematics Ex 1.3
Question 1.
Fill in the blanks
Question (i)
The compound interest on ₹ 5000 at 12% p.a for 2 years compounded annually is ………..
Answer:
₹ 1272
Hint:
Compound Interest (Cl) formula is
Cl = Amount – Principal
Amount = A (1 + \(\frac{r}{100}\))n = 5000 (1 + \(\frac{12}{100}\))2
= 5000 (1 + \(\frac{112}{100}\))2 = 6272
∴ Cl = 6272 – 5000 = ₹ 1272
![]()
Question (ii)
The compound interest on ₹ 8000 at 10% p.a for 1 year, compounded half yearly is …………
Answer:
₹ 820
Hint:
Compound interest (CI) = Amount – Principal
∴ Amount = P (1 + \(\frac{r}{100}\))2n [2n as it is compounded half yearly]
r = 10% p.a, for half yearly r = 1 + \(\frac{10}{2}\) = 5
A = 8000 (1 + \(\frac{5}{100}\))2×1 = 8000 x (\(\frac{105}{100}\))2 = 8820
CI = Amount – principal
= 8820 – 8000 = ₹ 820
Question (iii)
The annual rate of growth in population of a town is 10%. If its present population is 26620, the population 3 years ago was ………..
Answer:
₹ 20,000
Hint:
Rate of growth of population r = 10%; Present population = 26620
Let population 3 years ago be x
∴ Applying the formula for population growth which is similar to compound interest,
26620 = x (1 + \(\frac{r}{100}\))3
∴ 26620 = x (1 + \(\frac{10}{100}\))3 = x (\(\frac{110}{100}\))3
∴ x = 26620 x (\(\frac{110}{100}\))3
= ₹ 20,000
The population 3 years ago was ₹ 20,000
Questions (iv)
The amount if the compound interest is calculated quarterly, is found using the formula ………….
Answer:
A = P (1 + \(\frac{r}{400}\))4n
Hint:
Quarterly means 4 times in a year.
∴ The formula for compound interest is
A = P (1 + \(\frac{r}{400}\))4n
Question (v)
The difference between the S.I and C.I for 2 years for a principal of ₹ 5000 at the rate of interest 8% p.a is …….
Answer:
₹ 32
Hint:
Difference between S.I & C.I is given by the formula
CI – SI = P (\(\frac{r}{100}\))2
Principal (P) = 5000, r = 8% p.a
∴ CI – SI = 5000 (\(\frac{8}{100}\))2 = 5000 x \(\frac{8}{100}\) x \(\frac{8}{100}\) = ₹ 32
![]()
Question 2.
Say True or False
Question (i)
Depreciation value is calculated by the formula P (1 – \(\frac{r}{100}\))n
Answer:
True
Hint:
Depreciation formula is P (1 – \(\frac{r}{100}\))n
Question (ii)
If the present population of a city is P and it increases at the rate of r % p.a, then the population n years ago would be P (1 + \(\frac{r}{100}\))n.
Answer:
False
Hint:
Let the population ‘n’ yrs ago be ‘x’
Present population (P) = x × (1 + \(\frac{r}{100}\))n
x = \(\frac { P }{ (1+\frac { r }{ 100 } )^{ n } } \)
Question (iii)
The present value of a machine is ₹ 16800. It depreciates @25% p.a. Its worth after 2 years is ₹ 9450.
Answer:
True
Hint:
Present value of machine = ₹ 16800
Depreciation rate (n) = 25%
Value after 2 years = P (1 – \(\frac{r}{100}\))n = 16800 (1 – \(\frac{25}{100}\))2
= 16800 x (1 – \(\frac{1}{4}\))2 = 16800 x \(\frac{3}{4}\) x \(\frac{3}{4}\) = 9450
Question (iv)
The time taken for ₹ 1000 to become ₹ 1331 @20% p.a compounded annually is 3 years.
Answer:
False
Principal money = 1000
rate of interest Amount = 20%
Amount = 1331, applying in formula we get
A = (1 + \(\frac{r}{100}\))n
1331 = 1000(1 + \(\frac{r}{100}\))n
∴ \(\frac{1331}{1000}\) = (1 – \(\frac{1}{5}\))n
\(\frac{1331}{1000}\) = (\(\frac{6}{5}\))n
∴ n ≠ 3 (False)
![]()
Question (v)
The compound interest on ₹ 16000 for 9 months @20% p.a, compounded quarterly is ₹ 2522.
Answer:
True
Hint:
Principal (P) = 16000
n = 9 months = \(\frac{9}{12}\) years
r = 20% p.a
For compounding quarterly, we have to use below formula.
Amount (A) = P x (1 + \(\frac{r}{100}\))4n
Since quarterly we have to divide r by 4
r = \(\frac{20}{4}\)
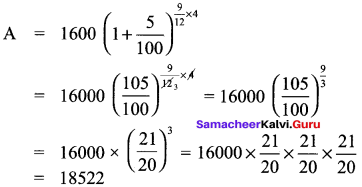
∴ Interest = A – P = 18522 – 16000 = 2522 (True)
Question 3.
Find the compound interest on ₹ 3200 at 2.5% p.a for 2 years, compounded annually.
Solution:
Principal (P) = ₹ 3200
r = 2.5% p.a
n = 2 years comp, annually
∴ Amount (A) = (1 + \(\frac{r}{100}\))n = (1 + \(\frac{2.5}{100}\))2
= 3200 x (1.025)2 = 3362
Compound interest (Cl) = Amount – Principal = 3362 – 3200 = ₹ 162
Question 4.
Find the compound interest for 2\(\frac{1}{2}\) years on ₹ 4000 at 10% p.a if the interest is compounded yearly.
Solution:
Principal (P) = ₹ 4000
r = 10% p.a
Compounded yearly n = 2\(\frac{1}{2}\) years. Since it is of the form a\(\frac{b}{c}\) years
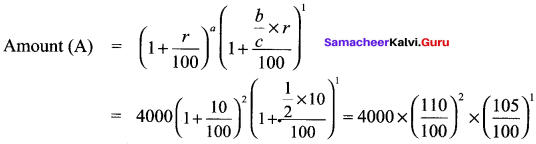
= 4000x 1.1 x 1.1 x 1.05 = 5082
∴ Cl = Amount – Principal = 5082 – 4000 = 1082
Question 5.
Magesh invested ₹ 5000 at 12% p.a for one year. If the interest is compounded half yearly, find the amount he gets at the end of the year.
Solution:
Principal (P) = ₹ 5000
Interest compounded half yearly
r = 12% p.a = \(\frac{12}{2}\) = 6% for half yearly
t = 1 yr.
Since compounded half yearly, the formula to be used is
Amount A = P (1 + \(\frac{r}{100}\))2n
A = 5000 (1 + \(\frac{6}{100}\))2×1 = 5000 x (\(\frac{106}{100}\))2 = ₹ 5618
Question 6.
At what time will a sum of ₹ 3000 will amount to ₹ 3993 at 10% p.a compounded annually?
Solution:
Amount A = ₹ 3993
Principal = ₹ 3000
r = 10% p.a
n = ?
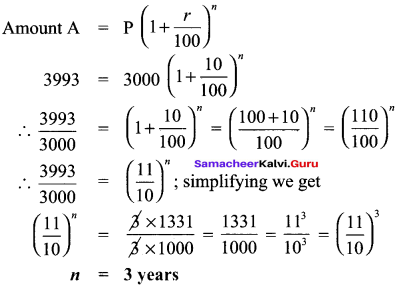
Question 7.
A principal becomes ₹ 2028 in 2 years at 4% p.a compound interest. Find the Principal.
Solution:
n = 2 years
r = rate of interest = 4% p.a
Amount A = ₹ 2028
Amount (A) = P (1 + \(\frac{r}{100}\))n
2028 = P (1 + \(\frac{4}{100}\))n
2028 = P (\(\frac{r}{100}\))2
∴ P = \(\frac{2028x100x100}{104×104}\) = ₹ 1875
![]()
Question 8.
At what rate percentage p.a will ₹ 5625 amount to ₹ 6084 in 2 years at compound interest?
Solution:
Principal (P) = ₹ 5625
Amount (A) = ₹ 6084
n = 2 years
r = ?
Amount (A) = P (1 + \(\frac{r}{100}\))n [Applying in formula]
6084 = 5625 (1 + \(\frac{r}{100}\))2
(1 + \(\frac{r}{100}\))2 = \(\frac{6084}{5625}\)
Taking square root on both sides, we get
1 + \(\frac{r}{100}\) = \(\frac{78}{75}\)
\(\frac{r}{100}\) = \(\frac{78}{75}\) – 1 = \(\frac{3}{75}\) = \(\frac{1}{25}\)
∴ r = \(\frac{1}{25}\) x 100 = 4%
Question 9.
In how many years will ₹ 3375 amount to ₹ 4096 at 13\(\frac{1}{3}\)% p.a where interest is compounded half-yearly?
Solution:
Principal = ₹ 3375
Amount = ₹ 4096
r = 13\(\frac{1}{3}\)% p.a = \(\frac{40}{3}\)% p.a
Compounded half yearly r = \(\frac { \frac { 40 }{ 3 } }{ 2 } \) = \(\frac{2}{3}\)
Let no. of years be n
for compounding half yearly, formula is

Question 10.
Find the C.I on ₹ 15000 for 3 years if the rates of interest is 15%, 20% and 25% for I, II and III years respectively.
Solution:
Principal (P) = ₹ 15000
rate of interest 1 (a) = 15% for year I
rate of interest 2 (b) = 20% for year II
rate of interest 3 (c) = 25% for year III
Formula for amount when rate of interest is different for different years is
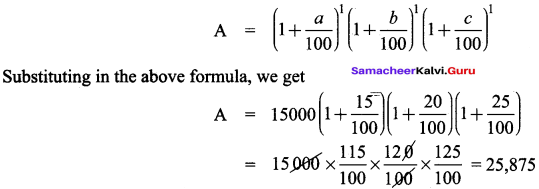
Compound Interest (Cl) = A – P = 25,875 – 15,000 = 10,875
Cl = ₹ 10,875
Question 11.
The present height of a tree is 847 cm. Find its height two years ago, if it increases at 10 % p.a.

Solution:
Present height of tree = 847 cm
Present height = ‘h’
n = 2 yrs
rate of growth = 10% p.a
Applying in formula, we get

∴ Original height of tree = 70 cm
Question 12.
Find the difference between the C.I and the S.I on ₹ 5000 for 1 year at 2% p.a, if the interest is compounded half yearly.
Solution:
Principal (P) = ₹ 5000
time period (n) = 1 yr.
Rate of interest (r) = 2% p.a
for half yearly r = 1%
Difference between Cl & SI is given by the formula
CI – SI = P (\(\frac{r}{100}\))2n [for half yearly compounding]
CI – SI = P (\(\frac{1}{100}\))2×1
= 5000 x \(\frac{1}{100}\) x \(\frac{1}{100}\) = ₹ 0.50
![]()
Question 13.
What is the difference in simple interest and compound interest on 115000 for 2 years at 6% p.a compounded annually.
Solution:
Principal (P) = ₹ 15,000
Time period (n) = 2 yrs.
Rate of interest (r) = 6% p.a compounded annually
Difference between CI and SI given by
CI – SI = P (\(\frac{r}{100}\))n = 15000 (\(\frac{6}{100}\))2
= 15000 x \(\frac{6}{100}\) x \(\frac{6}{100}\)
= ₹ 54
Question 14.
Find the rate of interest if the difference between the C.I and S.I on ₹ 8000 compounded annually for 2 years is ₹ 20.
Solution:
Principal (P) = ₹ 8000
time period (n) = 2 yrs.
rate of interest (r) = ?
Difference between Cl & SI is given by the formula
CI – SI = P (1 + \(\frac{r}{100}\))n
Difference between Cl & SI is given as 20
∴ 20 = 8000 x (\(\frac{r}{100}\))2
∴ (\(\frac{r}{100}\))2 = \(\frac{20}{8000}\) = \(\frac{1}{400}\)
Taking square root on both sides
\(\frac{r}{100}\) = \(\sqrt { \frac { 1 }{ 400 } } \) = \(\frac{1}{20}\)
∴ r = \(\frac{100}{20}\)
Question 15.
Find the principal if the difference between C.I and S.I on it at 15% p.a for 3 years is ₹ 1134.
Solution:
Rate of interest (r) = 15% p.a
time period (n) = 3 years
Difference between Cl & SI is given as 1134
Principal = ? → required to find
Simple Interest SI = \(\frac{Pnr}{100}\)
Compound Interest CI = P (1 + i)n – P
Cl – SI = P [(1 + i)n – 1 – \(\frac{nr}{100}\)]

Objective Type Questions
Question 16.
The number of conversion periods, if the interest on a principal is compounded every two months is ……………
(a) 2
(b) 4
(c) 6
(d) 12
Answer:
(c) 6
Hint:
Conversion period is the time period after which the interest is added to the principal. If principal is compounded every two months then in a year, there will be 6\(\frac{12}{2}\) conversation periods.
Question 17.
The time taken for ₹ 4400 to become ₹ 4851 at 10%, compounded half yearly is
(a) 6 months
(b) 1 year
(c) 1\(\frac{1}{2}\) years
(d) 2years
Answer:
(b) 1 year
Hint:
Principal = ₹ 4400
Amount = ₹ 4851
Rate of interest = 10% p.a
for half yearly, divide by 2,
r = \(\frac{10}{2}\) = 5 %
Compounded half yearly, so the formula is
A = P (1 + \(\frac{r}{100}\))2n
Substuting in the above formula, we get

Taking square root on both sides, we get
(\(\frac{21}{20}\))2n = (\(\frac{21}{20}\))2
Equating power on both sides
∴ 2n = 2,
n = 1
![]()
Question 18.
The cost of a machine is ₹ 18000 and it depreciates at 16\(\frac{2}{3}\)% annually. Its value after 2 years will be ………..
(a) ₹ 12000
(b) ₹ 12500
(c) ₹ 15000
(d) ₹ 16500
Answer:
(b) ₹ 12500
Hint:
Cost of machine = ₹ 18000
Depreciation rate = 16\(\frac{2}{3}\)% = \(\frac{50}{3}\)% p.a
time period = 2 years
∴ As per depreciation formula,
Depriciated value = Original value (1 – \(\frac{r}{100}\))n
Substituting in above formula, we get
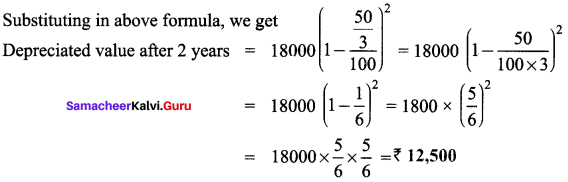
Question 19.
The sum which amounts to ₹ 2662 at 10% p.a in 3 years compounded yearly is ………..
(a) ₹ 2000
(b) ₹ 1800
(c) ₹ 1500
(d) ₹ 2500
Answer:
(a) ₹ 2000
Hint:
Amount = ₹ 2662
rate of interest = 10% p.a
Time period = 3 yrs. Compounded yearly
Principal (P) → required to find?
Applying formula A = P (1 + \(\frac{r}{100}\))n
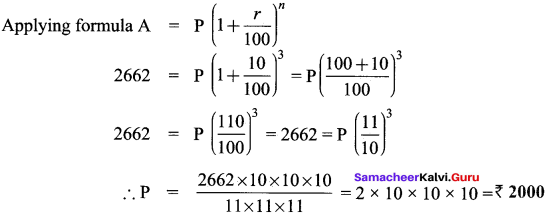
Question 20.
The difference between simple and compound interest on a certain sum of money for 2 years at 2% p.a is ₹ 1 the sum of money is ……….
(a) ₹ 2000
(b) ₹ 1500
(c) ₹ 3000
(d) ₹ 2500
Answer:
(d) ₹ 2500
Difference between Cl and SI is given as Re 1
Time period (n) = 2 yrs.
Rate of interest (r) = 2% p.a
Formula for difference is
CI – SI = P x (1 + \(\frac{r}{100}\))n
Substituting the values in above formula, we get
1 = P x (\(\frac{2}{100}\))2
∴ P = 1 x (\(\frac{100}{2}\))2
= 1 x (50)2 = ₹ 2500