Students can Download Maths Chapter 1 Life Mathematics Ex 1.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 1 Life Mathematics Ex 1.4
Miscellaneous Practise Problems
Question 1.
Nanda’s marks in 3 Math tests Tl, T2 and T3 were 38 out of 40,27 out of 30 and 48 out of 50. In which test did he do well? Find his overall percentage in all the 3 tests.
Solution:
Nanda’s marks are as follows
In Test 1 → T1 \(\frac{38}{40}\)
Test 2 → T2 \(\frac{27}{30}\)
Test 3 → T3 \(\frac{48}{50}\)
For percentage, multiply by 100
T1 = \(\frac{38}{40}\) x 100 = 95%
T2 = \(\frac{27}{30}\) x 100 = 90%
T3 = \(\frac{48}{50}\) x 100 = 96%
Hence, he has scored highest percentage in test 3
∴ He is done well in T3
Overall percentage is the average of the 3 percentages.
i.e \(\frac{90+95+96}{3}\) = \(\frac{281}{50}\) = 93\(\frac{2}{3}\)%
![]()
Question 2.
Sultana bought the following things from a general store. Calculate the total bill amount to be paid by her.
(i) Medicines costing ₹ 800 with GST @ 5% ………..

(ii) Cosmetics costing ₹ 650 with GST @ 12% ………….

(iii) Cereals costing ₹ 900 with GST @ 0% …………

(iv) Sunglass costing ₹ 1750 with GST @ 18 % ………..

(v) Air Conditioner costing ₹ 28500 with GST @ 28% ………..

Solution:

(i) Medicine : bill amount is 800(1 + \(\frac{5}{100}\)) = 800 x \(\frac{105}{100}\) = 840
(ii) Cosmetics: Bill amount is 650(1 + \(\frac{12}{100}\)) = 650 x \(\frac{112}{100}\) = 728
(iii) Cereals : Bill amount is 900(1 + \(\frac{0}{100}\)) = 900
(iv) Sunglass: bill amount is 1750(1 + \(\frac{18}{100}\)) = 1750 x \(\frac{118}{100}\) = 2065
(v) AC : Bill amount is 28500(1 + \(\frac{28}{100}\)) = 28500 x \(\frac{128}{100}\) = 36480
∴ Total bill amount = 840 + 728 + 900 + 2065 + 36480
= ₹ 41,013 (total bill amount)
Question 3.
P’s income is 25% more than that of Q. By what percentage is Q’s income less than P’s?
Solution:
Let Q’s income be 100.
P’s income is 25% more than that of Q
∴ P’s income = 100 + \(\frac{25}{100}\) x 100 = 125
Q’s income is 25 less than that of P
In percentage terms, Q’s income is less than P’s with respect to P’s income is
\(\frac{P-Q}{P}\) x 100 = \(\frac{125-100}{125}\) x 100 = \(\frac{25}{100}\) x 100 = 20%
Question 4.
Gopi sold a laptop at 12% gain. If it had been sold for ₹ 1200 more, the gain would have been 20%. Find the cost price of the laptop.

Solution:
Let the cost price of the laptop be ‘x’
Gain = 12%
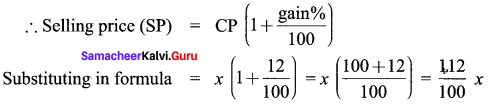
If the selling price was 1200 more
i.e \(\frac{112}{100}\)x +1200, the gain is 20%
i.e new selling price = x(1 + \(\frac{2}{100}\))
= \(\frac{112}{100}\)x + 1200 = x(100 + \(\frac{20}{100}\)) = \(\frac{112}{100}\)x
∴ 1200 = \(\frac{120}{100}\)x = \(\frac{112}{100}\)x = \(\frac{8}{100}\)x
∴ x = \(\frac{120×100}{8}\) = 15000
Cost price of the laptop is ₹ 15000
Question 5.
Vaidegi sold two sarees for ₹ 2200 each. On one she gains 10% and on the other she loses 12%. Calculate her gain or loss percentage in the sales.

Solution:
Saree 1:
The selling price is ₹ 2200, let cost price be CP1, gain is 10%
Cost price ₹ Using the formula

Saree 2:
The selling price is 2200, let cost price be CP2, loss is given as 12%. We need to find CP2 using the formula as before,

Cost price of both together is CP1 + CP2
= 2000 + 2500 = 4500 ……(1)
Selling price of both together is 2 x 2200 = 4400 …….(2)
Since net selling price is less than net cost price, there is a loss.
loss% = \(\frac{loss}{cost price}\) x 100
Loss = Net cost price – Net selling price
(1) – (2) = 4500 – 4400 = 100
∴ loss% = \(\frac{100}{4500}\) x 100 = \(\frac{100}{45}\) = \(\frac{20}{9}\) = 2\(\frac{2}{9}\)%
= 2\(\frac{2}{9}\)% loss
![]()
Question 6.
A sum of money becomes ₹ 18000 in 2 years and ₹ 40500 in 4 years on compound interest. Find the sum.
Solution:
Let the sum of money be ‘P’
Given that sum ‘P’ becomes 18000 in 2yrs.
i.e Amount (A) = P(1 + \(\frac{r}{100}\))n
18000 = P(1 + \(\frac{r}{100}\))2
(1 + \(\frac{r}{100}\))2 = \(\frac{18000}{P}\) ⇒ (1 + \(\frac{r}{100}\))4 = (\(\frac{18000}{P}\))2 ……(1)
Also given that sum ‘P’ becomes46500 in 4 yrs.
i.e Amount (A) = P(1 + \(\frac{r}{100}\))n
40500 = P(1 + \(\frac{r}{100}\))4
Substituting (1) in (2), we get
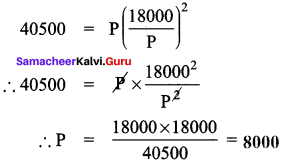
Question 7.
Find the difference in the compound interest on ₹ 62500 for 1\(\frac{1}{2}\) years at 8% p.a compounded annually and when compounded half-yearly.
Solution:
Case 1:
P = ₹ 62500
n = 1\(\frac{1}{2}\)yrs. (a\(\frac{b}{c}\)) formula
r = 8% Compound annully
CI = A – P

CI = A – P = 70200 – 62500 = 7700 ……(1)
CAse 2:
P = ₹ 62500
n = 1\(\frac{1}{2}\)yrs.
r = 8% p.a when compound half yearly
r = 4% compound half yearly

= 70304 – 62500 = ₹ 7804
Difference between case 1 & case 2 is (2) – (1)
∴ (2) – (1) = 7804 – 7700 = ₹ 104
Challenging Problems
Question 8.
If the first number is 20% less than the second number and the second number is 25% more than 100, then find the first number.
Solution:
Second number is 25% more than 100
∴ 2nd number is 100 + \(\frac{25}{100}\) x 100= 125
First number is 20% less than second no.
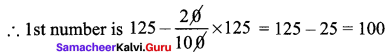
1st number is 100
Question 9.
A shopkeeper gives two successive discounts on an article whose marked price is ? 180 and selling price is ? 108. Find the first discount percent if the second discount is 25%.
Solution:
Marked price is given as ? 180
Let 1st discount be d1% = ? (to find)
2nd discount be d2% = 25%
Selling price is 108 (given)
Price after 1st discount = 180(1 – \(\frac { d_{ 1 } }{ 100 } \)) = P1
Price after 2nd discount = P1(1 – \(\frac { d_{ 2 } }{ 100 } \)) = 108
Substituting for P1 from (1), we get
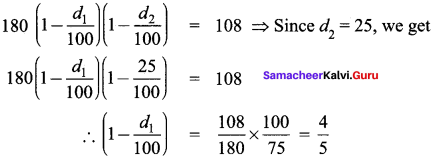
∴ 1 – \(\frac { d_{ 1 } }{ 100 } \) = \(\frac{4}{5}\)
∴ \(\frac { d_{ 1 } }{ 100 } \) = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)
∴ d1 = \(\frac{1}{5}\) x 100 = 20%
![]()
Question 10.
A man bought an article on 30% discount and sold it at 40% more than the marked price. Find the profit made by him.
Solution:
Let marked price be ‘P’
Discounted price = P(1 – \(\frac{d}{100}\)) where d is the discount %
∴ Discounted price = P(1 – \(\frac{30}{100}\)) = \(\frac{70}{100}\)P → this is the cost price.
Selling price = 40% more than marked price

Question 11.
Find the rate of compound interest at which a principal becomes 1.69 times itself in 2 years.
Solution:
Let principal be ‘P’
Amount is given to be 1.69 times principal
i.e 1.69 P
Time period is 2yrs. = (n)
Rate of interest = r = ? (required)
Applying the formula,
Amount = Principal (1 + \(\frac{r}{100}\))n
Substituting, 1.69 P = P (1 + \(\frac{r}{100}\))2
∴ (1 + \(\frac{r}{100}\))2 = \(\frac{1.69P}{P}\)
Taking square root on both sides, we get
\(\sqrt{1.69}\) = 1 + \(\frac{r}{100}\)
∴ 1 + \(\frac{r}{100}\) = 1.3
∴ \(\frac{r}{100}\) = 1.3
r = 30%
∴ rate of compound interst is 30%
![]()
Question 12.
The simple interest on a certain principal for 3 years at 10% p.a is ₹ 300. Find the compound interest accrued in 3 years.
Solution:
Let principal be ‘P’
Rate of interest is 10% p.a (r)
Time period (n) = 3 yrs.
Formula for simple interest
∴ P = \(\frac{300×100}{10×3}\) = 1000
Compound Interest = CI = A – P
Amount (A) = P (1 + \(\frac{r}{100}\))n
= 1000(1 + \(\frac{10}{100}\))3 = 1000 x (\(\frac{10o+10}{100}\))3
= 1000 x \(\frac{110}{100}\) x \(\frac{110}{100}\) x \(\frac{110}{100}\) = 1331
Compound Interest (Cl) = Amount – Principal
= 1331 – 1000 = 331
Compound Interest = ₹ 331