Students can Download Maths Chapter 2 Algebra Ex 2.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 2 Algebra Ex 2.5
Miscellaneous Practice Problems
Question 1.
The sum of three numbers is 58. The second numberis three times of two-fifth of the first number and the third number is 6 less than the first number. Find the three numbers.
Solution:
Here what we know
a + b + c = 58 (sum of three numbers is 58)
Let the first number be ‘x’
b = a + 3 (the second number is three times of \(\frac{1}{2}\) of the first number)
b = 3 x \(\frac{2}{5}\)x = \(\frac{6}{5}\)x
Third number = x – 6
Sum of the numbers is given as 58.
∴ x + \(\frac{6}{5}\)x + (x – 6) = 58
Multiplying by 5 throughout, we get
5 × x + 6x + 5 × (x – 6) = 58 x 5
5x + 6x + 5x – 30 = 290
∴ 16x = 290 + 30
∴ 16x = 320
∴ x = \(\frac{320}{16}\)x = 20
Answer:
1st number =20
2nd number = 3 x \(\frac{2}{5}\) x 20 = 24
3rd number = 24 – 6 = 14
![]()
Question 2.
In triangle ABC, the measure of ∠B is two third the measure of ∠A. The measure of ∠C is 20° more than the measure of ∠A. Find the measures of the three angles.
Solution:
Let angle ∠A be a°
Given that ∠B = \(\frac{2}{3}\) x ∠A = \(\frac{2}{3}\)a
& given ∠C = ∠A + 20 = a + 20
Since A, B & C are angles of a triangle, they add up to 180° (∆ property)
∠A + ∠B + ∠C = 180°
a + \(\frac{2}{3}\) a + a + 20 = 180°
\(\frac{3a+2a+3a}{3}\) + 20 = 180°
\(\frac{8a}{3}\) = 180 – 20 = 160°

∠C = 80°
Question 3.
Two equal sides of an isosceles triangle are 5y – 2 and 4y + 9 units. The third side is 2y + 5 units. Find y and the perimeter of the triangle.
Solution:
Given that 5y – 2 & 4y + 9 are the equal sides of an isosceles triangle.
The 2 sides are equal
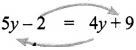
∴ 5y – 4y = 9 + 2 (by transposing)
∴ y = 11
∴ 1st side = 5y – 2 = 5 x 11-2 = 55 – 2 = 53
2nd side = 53
3rd side = 2y + 5 = 2 x 11 + 5 = 22 + 5 = 27
Perimeter is the sum of all 3 sides
∴ P = 53 + 53 + 27 = 133 units
Question 4.
In the given figure, angle XOZ and angle ZOY form a linear pair. Find the value of x.
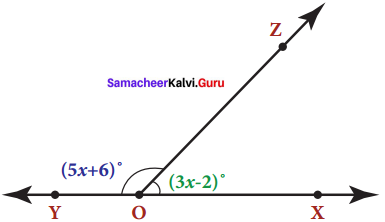
Solution:
Since ∠XOZ & ∠ZOY form a linear pair,
by property, we have their sum to be 180°
∴ ∠XOZ + ∠ZOY = 180°
3x – 2 + 5x + 6 = 180°
8x + 4 = 180 = 8x = 180 – 4
∴ 8x = 176 ⇒ x = \(\frac{176}{8}\) ⇒ x = 22°
XOZ = 3x – 2 = 3 x 22 – 2 = 66 – 2 = 64°
YOZ = 5x + 6 = 5 x 22 + 6
= 110 + 6 = 116
![]()
Question 5.
Draw a graph for the following data:

Does the graph represent a linear relation?
Solution:
Graph between side of square & area
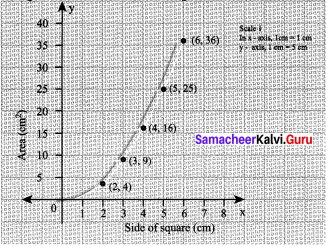
When we plot the graph, we observe that it is not a linear relation.
Challenging Problems
Question 6.
Three consecutive integers, when taken in increasing order and multiplied by 2, 3 and 4 respectively, total up to 74. Find the three numbers.
Solution:
Let the 3 consecutive integers be ‘x’, ’x + 1 & ‘x + 2’
Given that when multiplied by 2, 3 & 4 respectively & added up, we get 74
![]()
Simplifying the equation, we get
2x + 3x + 3 + 4x + 8 = 74
9x + 11 = 74
9x = 63 ⇒ x = \(\frac{63}{9}\) = 7
First number = 7
Second numbers = x + 1
Third numbers = x + 2
∴ The numbers are 7, 8 & 9
![]()
Question 7.
331 students went on a field trip. Six buses were filled to capacity and 7 students had to travel in a van. How many students were there in each bus?
Solution:
Let the number of students in each bus be ‘x’
number of students in 6 buses = 6 × x = 6x
Apart from 6 buses, 7 students went in van
A total number of students is 331
∴ 6x + 7 = 331
∴ 6x = 331 – 7 = 324
∴ x = \(\frac{324}{6}\) = 54
∴ There are 54 students in each bus.
Question 8.
A mobile vendor has 22 items, some which are pencils and others are ball pens. On a particular day, he is able to sell the pencils and ball pens. Pencils are sold for ₹ 15 each and ball pens are sold at ₹ 20 each. If the total sale amount with the vendor is ₹ 380, how many pencils did he sell?
Solution:
Let vendor have ‘p’ number of pencils & ‘b’ number of ball pens
Given that total number of items is 22
∴ p + b = 22
Pencils are sold for ₹ 15 each & ball pens for ₹ 20 each
total sale amount = 15 x p + 20 x b
= 15p + 20b which is given to be 380.
∴ 15p + 20b = 380
Dividing by 5 throughout,
\(\frac{15p}{5}\) + \(\frac{20b}{5}\) = \(\frac{380}{5}\)
⇒ 3p + 4b = 76
Multiplying equation (1) by 3 we get
3 x 7 + 3 x b = 22 x 3
⇒ 3p + 3b = 66
Equation (2) – (3) gives

∴ b = 10
∴ p = 12
He sold 12 pencils
![]()
Question 9.
Draw the graph of the lines y = x, y = 2x, y = 3x and y = 5x on the same graph sheet. Is there anything special that you find in these graphs?
Solution:
- y = x
- y = 2x
- y = 3x
- y = 5x
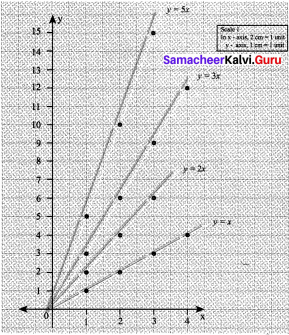
1. y = x
When x = 1, y = 1
x = 2, y = 2
x = 3, y = 2
2. y = 2x
When x = 1, y = 2
X = 2, y = 4
X = 3, y = 6
3. y = 3x
when x = 1, y = 3
x = 2, y = 6
x = 3, y = 9
4. y = 5x
When x = 1, y = 5
x = 2, y = 10
x = 3, y = 15
When we plot the alijpve points & join the points to form line, we notice that the lines become progressively steeper. In other words, the slope keeps increasing.
Question 10.
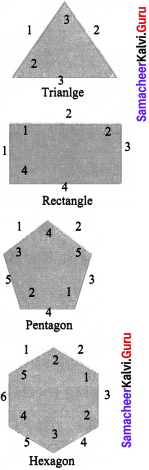
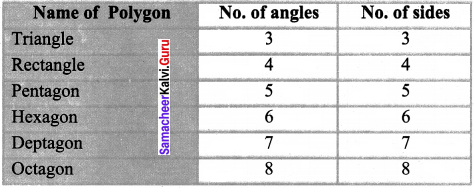
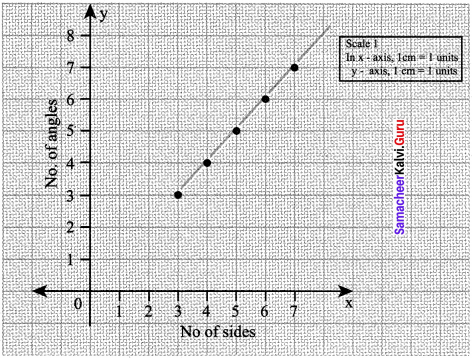
Consider the number of angles of a convex polygon and the number of sides of that polygon. Tabulate as follows:

Use this draw a graph illustrating the relations hip between the number of angles and the number of sides of a polygon.
Solution:
Angles: