Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 3 Geometry Additional Questions

Students can Download Maths Chapter 3 Geometry Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 3 Geometry Additional Questions

Question 1.
State Pythagoras theorem.
Solution:
In a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.

Question 2.
Write two uses of Pythagoras theorem in our daily life.
Solution:
The Pythagoras theorem is useful in finding the distance and the heights of objects.

Question 3.
Prove Pythagoras theorem.
Solution:
Proof of the Pythagoras theorem using similarity of triangles.

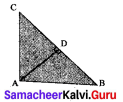
Given: ∠BAC = 90°
To Prove BC² = AB² + AC²
Construction: Draw AD ⊥ BC
Proof:

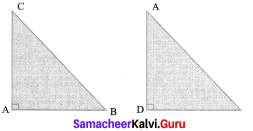
In ∆ ABC and ∆ DBA
∠B is common and ∠BAC = ∠ADB = 90°
Therefore, ∆ ABC ~ ∆ DBA, (AA similarity)
Hence, the ratio of corresponding sides are equal.
⇒ \(\frac{AB}{DB}\) = \(\frac{BC}{BA}\)
⇒ AB² = BC x DB
Similarity, ∆ ABC ~ ∆ DAC,
⇒ \(\frac{AC}{DC}\) = \(\frac{BC}{AC}\)
⇒ AC² = BC x DB
Adding (1) and (2), we get
AB² + AC² = BC x DB + BC x DC
= BC x (DB + DC) = BC x BC
⇒ AB² + AC² = BC² and hence the proof of the theorem

Question 4.
State the converse of Pythagoras theorem.
Solution:
If in a triangle, the square on the greatest side is equal to the sum of squares on the other two sides, then the triangle is right angled triangle.

Question 5.
Give 2 examples for Pythagorean triplet.
Solution:
(21, 28, 35), (24, 32, 40)

Question 6.
Check whether (2, 3, 5) is Pythagorean triplet.
Solution:

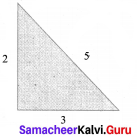
2² + 3² = 4 + 9 = 13
5² = 25
13 ≠ 25
∴ It is not a Pythagorean triplet.

Question 7.
Can the sides that measure 15 cm, 20 cm and 25 cm make a right triangle?
Solution:

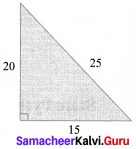
20² + 15² = 400 + 225 = 625
25² = 625
20² + 15² = 25²
∴ It is Pythagorean triplet.
∴ The given sides make a right angled triangle.

Question 8.
In the figure, find the value of x.

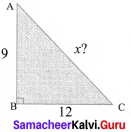
Solution:
In ABC
12² + 9² = 144 + 81 =225 = 15²
∴ x = 15

Question 9.
In the figure find the value of a and b and verify ∆ ABD is a right angled triangle.
Solution:
Now by altitude – on – hypotenuse theorem,
AB² = BC x BD gives
10² = a x 26
a = \(\frac{100}{26}\) = \(\frac{50}{13}\)

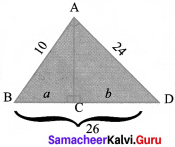
and AD² = CD x BD
24² = b x 26
b = \(\frac{576}{26}\) = \(\frac{288}{13}\)
and in ∆ ABD;
AB² + AD² = BD²
10² + 24² = 576 = 26²
BD = 26
Therefore ∆ ABD is a right angled triangle.

Question 9.
State the altitude-on-Hypotenuse theorem.
Solution:
If an altitude is drawn to the hypotenuse of an right angled triangle then (i) the two triangles are similar to the given triangle and also to each other.

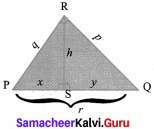
That is ∆ PRQ ~ ∆ PSR ~ ∆ RSQ

1. h² = xy
2. p² = yr and
3. q² = xr, where r = x + y