Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 3 Geometry Intext Questions

Students can Download Maths Chapter 3 Geometry Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 3 Geometry Intext Questions

Exercise 3.1
Try This (Text book Page No. 60)

Question 1.
How will you prove ∆ ABC ~ AD AC?
Proof:
In ∆ ABC & ∆ DAC, ∠C is common and ∠BAC = ∠ADC = 90°
Therefore ∆ ABC ~ AD AC (AA similarity)

Try This (Text book Page No. 61)

Question 1.
Check whether the following are Pythagorean triplets

1. 57, 176, 185
2. 264, 265, 23
3. 8, 41, 40

Solution:
1. For Pythagorean triplet, the sum of the squares of 2 sides is equivalent to square of 3rd side (hypotenuse)
Let us check of
57² + 176² whether = 185² or not
57² = 3249
176² = 30976
185² = 34225
57² + 176² = 3249 + 30976 = 34225 = 185²
∴ 57, 176 & 185 are Pythagorean triplet.

2. 23, 264, 265
23² = 529
264² = 69696
23² + 264² = 70225
265² = 70225
∴ 23² + 264² = 265²
∴ Pythagorean triplet

3. 8, 41, 40
8² = 64
40² = 1600
8² + 40² = 1664
41² = 1681
8² + 40² ≠ 41² = 1
∴ They are not Pythagorean triplet

Activity – 1 (Text book Page No. 62)

We can construct sets of Pythagorean triplets as follows. Let m and n be any two positive integers (m > n):
(a, b, c) is a Pythagorean triple if a = m² – n², b = 2mn and c = m² + n² (Think, why?) Complete the table.

Solution:

Activity – 2 (Text book Page No. 65)

Question 1.
Find all integer-sided right angled triangles with hypotenuse 85
Solution:
(x + y)² – 2xy = 85²

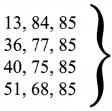
Pythagorean triplets with hypotenuse 85.

Exercise 3.3
Try These (Text book Page No. 68)

Question 1.
The area of the trepezium is ……..
Answer:
\(\frac{1}{2}\) x h x (a + b) sq. units!

Question 2.
The distance between the parallel sides of a trapezium is called as ………
Answer:
its height

Question 3.
If the height and parallel sides of a trapezium are 5 cm, 7 cm and 5 cm respectively, then its area is ……..
Answer:
30 sq cm
Hint:
= \(\frac{1}{2}\) x h x (a + b) sq. units
= \(\frac{1}{2}\) x 5 x (7 + 5)
= \(\frac{1}{2}\) x 5 x 12 = 30 sq.cm

Question 4.
In an isosceles trapezium, the non-parallel sides are ……….. in length.
Answer:
Equal.

Question 5.
To construct a trapezium, ………… measurements are enough.
Answer:
Four.

Question 6.
If the area and sum of the parallel sides are 60 cm2 and 12 cm, its height is ………..
Answer:
10 cm
Hint:
Area of the trapezium = \(\frac{1}{2}\) x h (a + b)
60 = \(\frac{1}{2}\) x h x (12)
h = \(\frac{60×2}{12}\) = 10 cm

Exercise 3.4
Think (Text book Page No. 74)

Question 1.
Can a rhombus, a square or a rectangle be called as a parallelogram? Justify your answer.
Solution:
Yes, a rhombus, a square or a rectangle can be called as parallelogram as the opposite sides are equal and parallel and diagonals bisect each other in this figures.

Try These (Text book Page No. 74)

Question 1.
In a parallelogram, the opposite sides are …….. and ……….
Answer:
equal, parallel

Question 2.
If ∠A of a parallelogram ABCD is 100° then, find ∠B, ∠C and ∠D .
Answer:

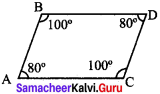
∠B = 80°
∠C = 100°
∠D = 80°

Question 3.
Diagonals of a parallelogram each other.
Answer:
Bisect

Question 4.
If the base and height of the parallelogram are 20 cm and 5 cm then, its area is ………
Answer:
100 sq.cm

Question 5.
Find the unknown values in the given parallelograms and write the property Used to find them.

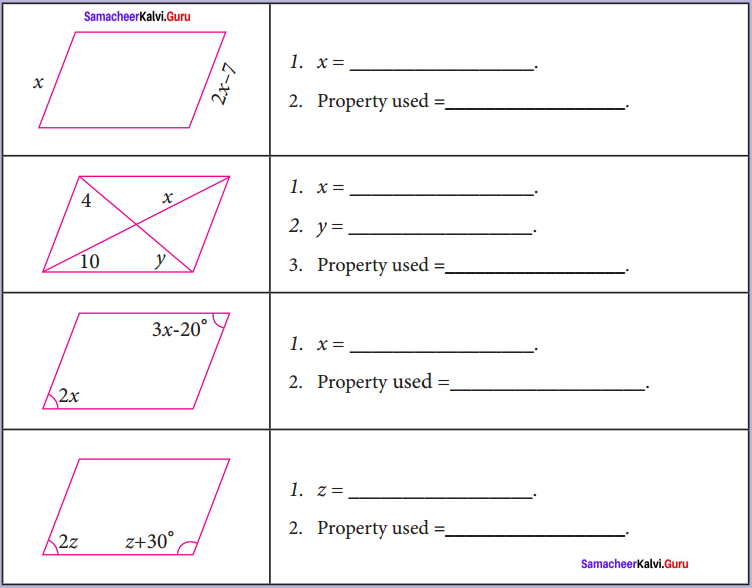
Solution: