Students can Download Maths Chapter 1 Numbers Ex 1.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 1 Numbers Ex 1.1
Question 1.
Fill in the blanks:
i. The ones digit in the square of 77 is …………
ii. The number of non-square numbers between 24² and 25² is ……………….
iii. If a number ends with 5, its square ends with …………
iv. A square number will not end with numbers ………….
v. The number of perfect square numbers between 300 and 500 is …………
Solution:
i. 9
ii. 48
iii. 5
iv. 2, 3, 7, 8
v. 5
![]()
Question 2.
Say True or False:
i. When a square number ends in 6, its square root will have 6 in the unit’s place.
ii. A square number will not have odd number of zeros at the end.
iii. The number of zeros in the square of 961000 is 9.
iv. (7, 24, 25) is a Pythagorean triplet.
v. The square root of 221 is 21.
Solution:
i. True
ii. True
iii. False
iv. True
v. False
Question 3.
What will be the ones digit in the squares of the following numbers?
(i) 36
(ii) 252
(iii) 543
Solution:
(i) If a number ends with 6, its square ends with 6.
∴ Ones’ digit in the square of 36 is 6.
(ii) If a number ends with 2, its square ends with 4.
∴ Ones’ digit in the square of 252 is 4
(iii) If a number ends with 3, its square ends with 9.
∴ Ones’ digit in the square of 543 is 9.
Question 4.
Study the given numbers and justify why each of them obviously cannot be a perfect square.
(i) 1000
(ii) 34567
(iii) 408
Solution:
We know that the numbers end with odd number of zeros, 7 and 8 not perfect squares.
∴ 1000, 34567 and 408 cannot be perfect squares.
Question 5.
Find the sum without actually adding the following odd numbers:
(i) 1 + 3 + 5 + 7 +……..+ 35
(ii) The first 99 odd natural numbers.
Solution:
1 + 3 + 5 + 7 +……..+ 35.
Here there are 18 odd numbers from 1 to 35.
Sum of first n consecutive odd natural numbers = n²
∴ Sum of first 18 consecutive odd natural numbers = 18² = 18 × 18 = 324
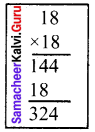
(ii) The first 99 odd natural numbers.
Sum of first n consecutive natural numbers = n²
∴ Sum of 99 odd natural numbers = 99² = 99 × 99 = 9801

Question 6.
Express
(i) 15² and
(ii) 19²
as the sum of two consecutive positive integers.
Solution:

![]()
Question 7.
Write
(i) 10² and
(ii) 11²
as the sum of consecutive odd natural numbers.
Solution:
(i) 10²
10² = 100 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(ii) 11²
11² = 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21
Question 8.
Find a Pythagorean triplet whose
(i) largest member is 65
(ii) smallest member is 10
Solution:
(i) Largest number is 65
Given largest number is 65.
We know that 2m, m² – 1, m² + 1 form a Pythagorean triplet.
let m² + 1 = 65
m² = 65 – 1
m² = 64
m² = 8 × 8
m = 8
∴ 2m = 2 × 8 = 16
m² – 1 = 64 – 1 = 63
∴ The required Pythagorean triplet is (16, 63, 65)
(ii) Smallest number is 10
We know that (2m, m² – 1, m² + 1) form a Pythagorean triplet.
Given smallest number is 10
let 2m = 10
m = \(\frac{10}{2}\)
m = 5
m² + 1 = 5² + 1 = 25 + 1 = 26
m² – 1 = 5² – 1 = 25 – 1 = 24
∴ The required Pythagorean triplet is (10, 24, 26)
Question 9.
Find the square root of the following by repeated subtraction method.
(i) 144
(ii) 256
(iii) 784
Solution:
(i) 144
Step 1: 144 – 1 = 143
Step 2: 143 – 3 = 140
Step 3: 140 – 5 = 135
Step 4: 135 – 7 = 128
Step 5: 128 – 9 = 119
Step 6: 119 – 11 = 108
Step 7: 108 – 13 = 95
Step 8: 95 – 15 = 80
Step 9: 80 – 17 = 63
Step 10: 63 – 19 = 44
Step 11: 44 – 21 = 23
Step 12: 23 – 23 = 0.
We get 0 in the 12th step.
∴ 144 is a perfect square and ⇒ \(\sqrt{144}\) = 12.
(ii) 256
Step 1: 256 – 1 = 255
Step 2: 255 – 3 = 252
Step 3: 252 – 5 = 247
Step 4: 247 – 7 = 240
Step 5: 240 – 9 = 231
Step 6: 231 – 11 = 220
Step 7: 220 – 13 = 207
Step 8: 207 – 15 = 192
Step 9: 192 – 17 = 175
Step 10: 175 – 19 = 156
Step 11: 156 – 21 = 135
Step 12: 135 – 23 = 112
Step 13: 112 – 25 = 87
Step 14: 87 – 27 = 60
Step 15: 60 – 29 = 31
Step 16: 31 – 31 = 0
We have subtracted odd numbers starting from 1 repeatedly from 256. We get 0 in the 8th step.
∴ 256 is a perfect square and \(\sqrt{256}\) = 16
(iii) 784
Step 1: 784 – 1 = 783
Step 2: 783 – 3 = 780
Step 3: 780 – 5 = 775
Step 4: 775 – 7 = 768
Step 5: 768 – 9 = 759
Step 6: 759 – 11 = 748
Step 7: 748 – 13 = 735
Step 8: 735 – 15 = 720
Step 9: 720 – 17 = 703
Step 10: 703 – 19 = 684
Step 11: 684 – 21 = 663
Step 12: 663 – 23 = 640
Step 13: 640 – 25 = 615
Step 14: 615 – 27 = 588
Step 15: 588 – 29 = 559
Step 16: 559 – 31 = 528
Step 17: 528 – 33 = 495
Step 18: 495 – 35 = 460
Step 19: 460 – 37 = 423
Step 20: 423 – 39 = 384
Step 21: 384 – 41 = 343
Step 22: 343 – 43 300
Step 23: 300 – 45 = 255
Step 24: 255 – 47 = 208
Step 25: 208 – 49 = 159
Step 26: 159 – 51 = 108
Step 27: 108 – 53 = 55
Step 28: 55 – 55 = 0
We have subtracted odd numbers starting from 1 repeatedly from 784, we get zero in the 28th step.
∴ 784 is a perfect square. \(\sqrt{784}\) = 28
![]()
Question 10.
Find the square root by prime factorisation method.
(i) 1156
(ii) 4761
(iii) 9025
Solution:
(i) 1156
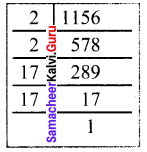
1156 = 2 × 2 × 17 × 17
1156 = 2² × 17²
1156 = (2 × 17)²
∴ \(\sqrt{1156}\) = \((\sqrt{2×17})^{2}\) = 2 × 17 = 34
∴ \(\sqrt{1156}\) = 34
(ii) 4761
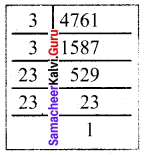
4761 = 3 × 3 × 23 × 23
4761 = 3² × 23²
4761 = (3 × 23)²
\(\sqrt{4761}\) = \((\sqrt{3 × 23})^{2}\)
\(\sqrt{4761}\) = 3 × 23
\(\sqrt{4761}\) = 69
(iii) 9025
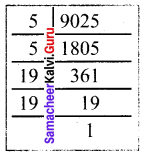
9025 = 5 × 5 × 19 × 19
9025 = 5² × 19²
9025 = (5 × 19)²
\(\sqrt{925}\) = \((\sqrt{5 × 19})^{2}\) = 5 × 19 = 95
Question 11.
Examine if each of the following is a perfect square:
(i) 725
(ii) 190
(iii) 841
(iv) 1089
Solution:
(i) 725
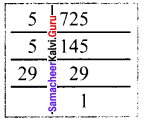
725 = 5 × 5 × 29 = 5² × 29
Here the second prime factor 29 does not have a pair.
Hence 725 is not a perfect square number.
(ii) 190
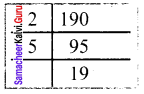
190 = 2 × 5 × 19
Here the factors 2, 5 and 9 does not have pairs.
Hence 190 is not a perfect square number.
(iii) 841
841 = 29 × 29
Hence 841 is a perfect square
(vi) 1089
1089 = 3 × 3 × 11 × 11 = 33 × 33

Hence 1089 is a perfect square
Question 12.
Find the least number by which 1800 should be multiplied so that it becomes a perfect square. Also, find the square root of the perfect square thus obtained.
Solution:

We find 1800 = 2 × 2 × 3 × 3 × 5 × 5 × 2
= 2² × 3² × 5² × 2
Here the last factor 2 has no pair. So if we multiply 1800 by 2, then the number becomes a perfect square.
∴ 1800 × 2 = 3600 is the required perfect square number.
∴ 3600 = 1800 × 2
3600 = 2² × 3² × 5² × 2 × 2
3600 = 2² × 3² × 5² × 2²
= (2 × 3 × 5 × 2)²
\(\sqrt{3600}\) = \((\sqrt{2 × 3 × 5 × 2})^{2}\) = 2 × 3 × 5 × 2 = 60
∴ \(\sqrt{3600}\) = 60.
![]()
Question 13.
Find the smallest number by which 10985 should be divided so that the quotient is a perfect square.
Solution:
We find 10985 = 5 × 13 × 13 × 13
= 5 × 13 × 13²
Here the prime factors 5 and 13 do not have pairs.
∴ We can divide 10985 by 65 (5 × 13) to get a perfect square
∴ When we divide 10985 by 65 we get quotient 169.
169 = 13 × 13
\(\sqrt{169}\) = 13
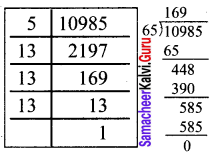
Question 14.
Is 2352 a perfect square? If not, find the smallest number by which 2352 must be multiplied so that the product is a perfect square. Find the square root of the new number.
Solution:

We find 2352 = 2 × 2 × 2 × 2 × 3 × 7 × 7
2352 = 2² × 2² × 3 × 7²
Here the factor 3 has no pair.
∴ 2352 is not a perfect square.
We have to multiply 2352 by 3 so that the product is a perfect square.
Img 13
∴ 2352 × 3 = 2² × 2² × 7² × 3 × 3
7056 = 2² × 2² × 7² × 3²
7056 = (2 × 2 × 7 × 3)²
∴ \(\sqrt{7056}\) = \((\sqrt{2 × 2 × 7 × 3})^{2}\)
= 2 × 2 × 7 × 3 = 84
\(\sqrt{7056}\) = 84
![]()
Question 15.
Find the least square number which is divisible by each of the numbers 8, 12 and 15.
Solution:
The least number divisible by each of the numbers 8, 12, 15 is their L.C.M
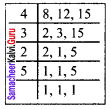
∴ LCM of 8, 12, 15 is (4 × 3 × 2 × 5) = 120
Resolving 120 into prime factors
We get 120 = 2 × 2 × 2 × 3 × 5
Grouping into pairs of equal factors
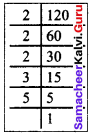
120 = (2 x 2) x 2 x 3 x 5
∴ The factors 2, 3 and 5 had no pairs.
Thus to make 120 a perfect square, we must multiply it by (2 x 3 x 5) = 30.
∴ The least square number divisible by 8,12 and 15 is 120 x 30 = 3600