Students can Download Maths Chapter 3 Geometry Ex 3.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 3 Geometry Ex 3.2
Miscellaneous and Practice Problems
Question 1.
Identify the centroid of ΔPQR.
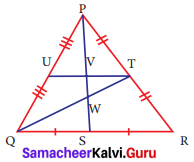
Solution:
In ΔPQR, PT = TR ⇒ QT is a median from vertex Q.
QS = SR ⇒ PS is a median from vertex P.
QT and PS meet at W and therefore W is the centroid of ΔPQR.
![]()
Question 2.
Name the orthocentre of ΔPQR.
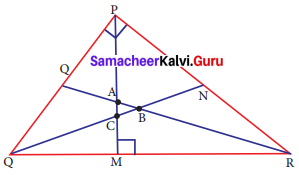
Solution:
∠P = 90°
This is a right triangle
∴ orthocentre = P [∴ In right triangle orthocentre is the vertex containing 90°]
Question 3.
In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. If the length of GA is 3 cm, find XA.
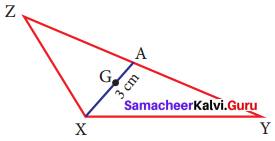
Solution:
Given A is the midpoint of YZ.
∴ ZA = AY
G is the centroid of ΔXYZ centroid divides each median in a ratio 2 : 1 ⇒ XG : GA = 2 : 1
\(\frac{XG}{GA}\) = \(\frac{2}{1}\)
\(\frac{XG}{3}\) = \(\frac{2}{1}\)
XG = 2 × 3
XG = 6 cm
XA = XG + GA
= 6 + 3 ⇒ XA = 9 cm
Challenging Problems
Question 4.
Find the length of an altitude on the hypotenuse of a right angled triangle of legs of length 15 feet and 20 feet.
Solution:
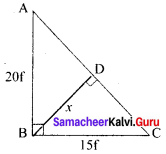
Since ∠B = 90°
Using pythagoras theorem
AC² = AB² + BC² = 20² + 15²
= 400 + 225
AC² = 625
AC² = 255
AC = 25
Area of a triangle ΔABC = \(\frac{1}{2}\) × 15 × 20 = 150 feet²
Again Area of ΔABC = \(\frac{1}{2}\) × AC × BD
150 = \(\frac{1}{2}\) × 25 × BD
BD = \(\frac{2 × 150}{25}\) = \(\frac{300}{25}\)
BD = 12 feet
∴ Length of the altitude on the hypotenuse of the right angled triangle is 12 feet.
Question 5.
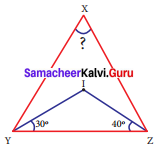
If I is the incentre of ΔXYZ, ∠IYZ = 30° and ∠IZY = 40°, find ∠YXZ.
Solution:
Since I is the incentre of ΔXYZ
∠IYZ = 30° ⇒ ∠IYX = 30°
∠IZY = 40° ⇒ ∠IZX = 40°
∴ ∠XYZ = ∠XYI + ∠IYZ = 30° + 30°
∠XYZ = 60°
lll ly ∠XYZ = ∠XZI + ∠IZY = 40° + 40°
∠XYZ = 80°
By angle sum property of a triangle
∠XZY + ∠XYZ + ∠YXZ = 180°
80° + 60° + ∠YXZ = 180°
140° + ∠YXZ = 180°
∠YXZ = 180° – 140°
∠YXZ = 40°
![]()
Question 6.
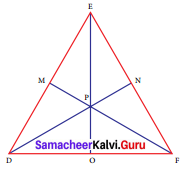
In ΔDEF, DN, EO, FM are medians and point P is the centroid. Find the following.
(i) If DE = 44, then DM = ?
(ii) If PD = 12, then PN = ?
(iii) If DO = 8, then FD = ?
(iv) If OE = 36, then EP = ?
Solution:
Given DN, EO, FM are medians.
∴ FN = EN
DO = FO
EM = DM
(i) If DE = 44, then
DM = \(\frac{44}{2}\) = 22
DM = 22
(ii) If PD = 12, PN = ?
\(\frac{PD}{PN}\) = \(\frac{2}{1}\)
\(\frac{12 }{PN}\) = \(\frac{2}{1}\) ⇒ PN = \(\frac{12}{2}\) = 6
PN = 6
(iii) If DO = 8, then
FD = DO + OF = 8 + 8
FD = 16
(iv) If OE = 36,
then \(\frac{EP}{PO}\) = \(\frac{2}{1}\)
\(\frac{EP}{2}\) = PO
OE = OP + PE
36 = \(\frac{PE}{2}\) + PE
36 = \(\frac{PE}{2}\) + \(\frac{2PE}{2}\)
36 = \(\frac{3PE}{2}\)
PE = \(\frac{36 × 2}{3}\)
PE = 24
![]()