Students can Download Maths Chapter 1 Rational Numbers Ex 1.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 1 Rational Numbers Ex 1.2
8th Maths Exercise 1.2 Question 1.
Fill in the blanks:
(i) The multiplicative inverse of \(2 \frac{3}{5}\) is _____.
(ii) If -3 × \(\frac{6}{-11}=\frac{6}{-11}\) × x, then x is _______.
(iii) If distributive property is true for \(\left(\frac{3}{5} \times \frac{-4}{9}\right)+\left(x \times \frac{15}{17}\right)=\frac{3}{5} \times(y+z)\), then x, y, z are _____, _____ and ____.
(iv) If x × \(\frac{-55}{63}=\frac{-55}{63}\) × x = 1, then x is called the _____ of \(\frac{55}{63}\).
(v) The multiplicative inverse of -1 is ______.
Solution:
(i) \(\frac{5}{13}\)
(ii) -3
(iii) \(\frac{3}{5}, \frac{-4}{9}\) and \(\frac{15}{13}\)
(iv) Mulitplicative inverse
(v) -1
8th Standard Maths Book Exercise 1.2 Question 2.
Say True or False.
(i) \(\frac{-7}{8} \times \frac{-23}{27}=\frac{-23}{27} \times \frac{-7}{8}\) illustrates the closure property of rational number.
(ii) Associative property is not true for subtraction of rational numbers.
(iii) The additive inverse of \(\frac{-11}{-17}\) is \(\frac{11}{17}\).
(iv) The product of two negative rational numbers is a positive rational number.
(v) The multiplicative inverse exists for all rational numbers.
Solution:
(i) False
(ii) True
(iii) False
(iv) True
(v) False
8th Standard Maths Exercise 1.2 Question 3.
Verify the closure property for addition and multiplication of the rational numbers \(\frac{-5}{7}\) and \(\frac{8}{9}\)
Solution:
Closure property for addition.
Let a = \(\frac{-5}{7}\) and b = \(\frac{8}{9}\) be the given rational numbers.
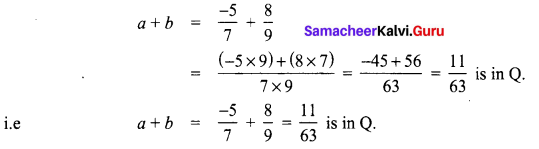
? Closure property is true for addition of rational numbers.
Closure property for multiplication
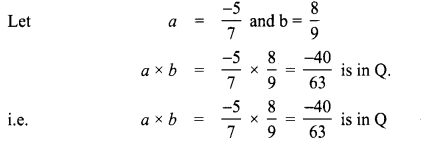
? Closure property is true for multiplication of rational numbers.
8th Std Maths Exercise 1.2 Question 4.
Verify the associative property for addition and multiplication of the rational numbers \(\frac{-10}{11}, \frac{5}{6}, \frac{-4}{3}\).
Solution:
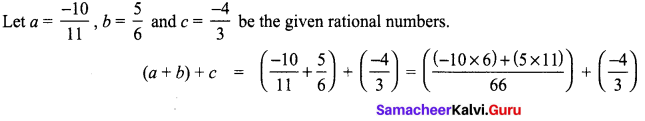

a × (b × c) = \(\frac{100}{99}\)
From (1) and (2) a × (b × c) = (a × b) × c is true for rational numbers.
Thus associative property is true for addition and multiplication of rational numbers.
Samacheer Guru 8th Maths Question 5.
Check the commutative property for addition and multiplication of the rational numbers \(\frac{-10}{11}\) and \(\frac{-8}{33}\).
Solution:
Let a = \(\frac{-10}{11}\) and b = \(\frac{-8}{33}\) be the given rational numbers.

From (1) and (2)
a + b = b + a and hence addition is commutative for rational numbers.
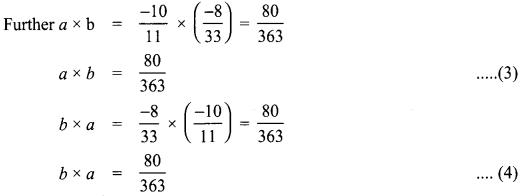
From (3) and (4) a × b = b × a
Hence multiplication is commutative for rational numbers.
Samacheerkalvi.Guru 8th Maths Question 6.
Verify the distributive property a × (b + c) = (a × b) + (a × c) for the rational numbers a = \(\frac{-1}{2}\) ,b = \(\frac{2}{3}\) and c = \(\frac{-5}{6}\).
Solution:
Given the rational number a = \(\frac{-1}{2}\) ,b = \(\frac{2}{3}\) and c = \(\frac{-5}{6}\).

From (1) and (2) we have a × (b + c) = (a × b) + (a × c) is true.
Hence multiplication is distributive over addition for rational numbers Q.
10th Maths Exercise 1.2 Samacheer Kalvi Question 7.
Evaluate:
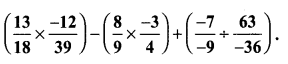
Solution:

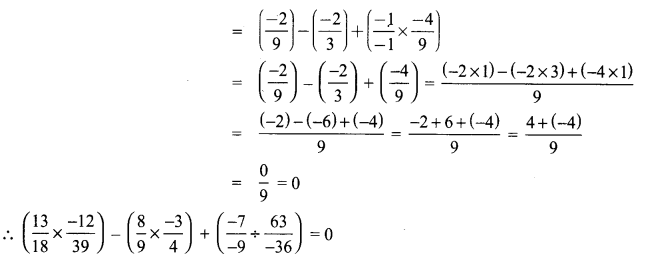
Samacheer Kalvi Guru 8th Standard Maths Question 8.
Evaluate using appropriate properties.

Solution:

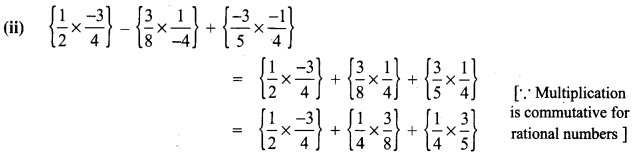
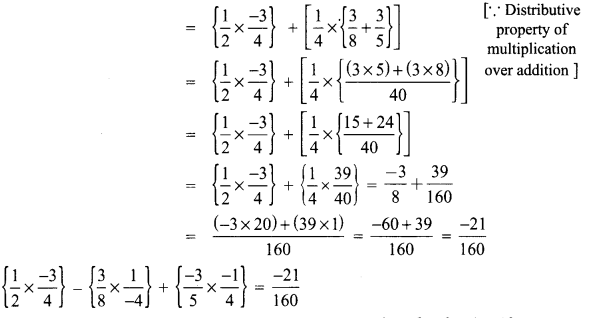
8th Maths 1.2 Question 9.
Use commutative and distributive properties to simplify \(\frac{4}{5} \times \frac{-3}{8}-\frac{3}{8} \times \frac{1}{4}+\frac{19}{20}\)
Solution:
Since multiplication is commutative
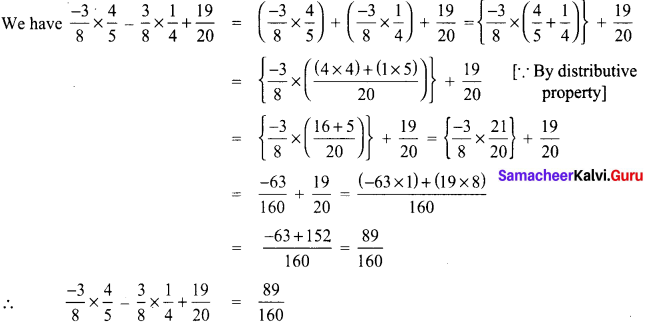
Objective Type Questions
8th Standard Maths 1.2 Question 10.
Mulitplicative inverse of 0 (is)
(A) 0
(B) 1
(C) -1
(D) does not exist
Solution:
(D) does not exist
8th Maths Book Example Sums Question 11.
Which of the following illustrates the inverse property for addition?
![]()
Solution:
(A) \(\frac{1}{8}-\frac{1}{8}\) = 0
Samacheer Kalvi 8th Books Maths Question 12.
Closure property is not true for division of rational numbers because of the number
(A) 1
(B) -1
(C) 0
(D) \(\frac{1}{2}\)
Solution:
(C) 0
Samacheer Kalvi Guru Maths 8th Question 13.
\(\frac{1}{2}-\left(\frac{3}{4}-\frac{5}{6}\right) \neq\left(\frac{1}{2}-\frac{3}{4}\right)-\frac{5}{6}\) illustrates that subtraction does not satisfy the ____ law of rational numbers.
(A) commutative
(B) closure
(C) distributive
(D) associative
Solution:
(D) associative
Samacheer Kalvi 8th Maths Question 14.
\(\left(1-\frac{1}{2}\right) \times\left(\frac{1}{2}-\frac{1}{4}\right) \div\left(\frac{3}{4}-\frac{1}{2}\right)\) = ______________

Solution:
(A) \(\frac{1}{2}\)