Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.5

Students can Download Maths Chapter 3 Algebra Ex 3.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.5

Miscellaneous Practice Problems

Question 1.
Subtract: -2(xy)² (y³ + 7x²y + 5) from 5y² (x²y³ – 2x⁴y + 10x²)
Solution:
5y² (x²y³ – 2x⁴y + 10x²) – [(-2)(xy)² (y³ + 7x²y + 5)]
= [5y² (x²y³) – 5y² (2x⁴y) + 5y² (10x²)] – [(-2)x²y² (y³ + 7x²y + 5)]
= (5y⁵5x² – 10x⁴y³ + 50x²y²)
= 5x²y⁵ – 10x⁴y³ + 50x²y² – [(-2x²y⁵) – 14x⁴y³ – 10x²y²]
= 5x²y⁵ – 10x⁴y³ + 50x²)y² + 2x² y⁵ + 14x⁴)y³ + 10x²)y²
= (5 + 2)x²y⁵ + (-10 + 14)x⁴y³ + (+50 + 10)x²y²
= 7x²y⁵ + 4x⁴y³ + 60x²y²

Question 2.
Multiply (4x² + 9) and (3x – 2).
Solution:
(4x² + 9) (3x – 2) = 4x²(3x – 2) + 9(3x – 2)
= (4x²)(3x) – (4x²)(2) + 9(3x) – 9(2) = (4 × 3 × x × x²) – (4 × 2 × x²) + (9 × 3 × x) – 18
= 12x³ – 8x² + 27x – 18 (4x³ + 9) (3x – 2) = 12x³ – 8x² + 27x – 18

Question 3.
Find the simple interest on Rs. 5a²b² for 4ab years at 7b% per annum.
Solution:

Question 4.
The cost of a note book is Rs. 10ab. If Babu has Rs. (5a²b + 20ab² + 40ab). Then how many note hooks can he buy?
Solution:
For ₹ 10 ab the number of note books can buy = 1.

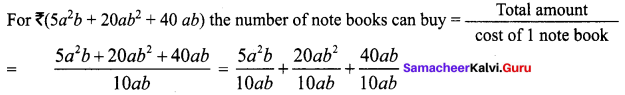
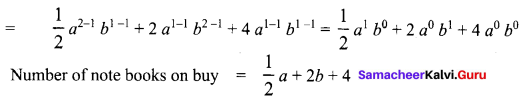
Question 5.
Factorise : (7y² – 19y – 6)
Solution:
7y² – 19y – 6 is of the form ax² + bx + c where a = 7; b = -19; c = – 6

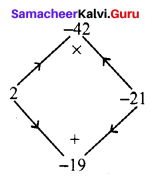
The product a × c = 7 × -6 = -42
sum b = – 19

The middle term – 19y can be written as – 21y + 2y
7y² – 19y – 6 = 7y² – 21y + 2y – 6
= 7y(y – 3) + 2(y – 3) = (y – 3)(7y + 2)
7y² – 19y – 6 = (y – 3)(7y + 2)

Challenging Problems

Question 6.
A contractor uses the expression 4x² + 11x + 6 to determine the amount of wire to order when wiring a house. If the expression comes from multiplying the number of rooms times the number of outlets and he knows the number of rooms to be (x + 2), find the number of outlets in terms of ‘x’ [Hint: factorise 4x² + 11x + 6]
Solution:
Given Number of rooms = x + 2
Number of rooms × Number of outlets = amount of wire.

Now factorising 4x² + 11x + 6 which is of the form ax² + bx + c with a = 4 b = 11 c = 6.
The product a × c = 4 × 6 = 24
sum b = 11


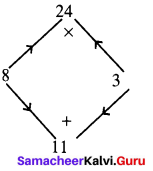
The middle term 11x can be written as 8x + 3x
∴ 4x² + 11x + 6 = 4x² + 8x + 3x + 6 = 4x (x + 2) + 3 (x + 2)
4x² + 11x + 6 = (x + 2) (4x + 3)
Now from (1) the number of outlets

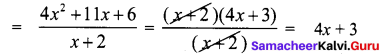
∴ Number of outlets = 4x + 3

Question 7.
A mason uses the expression x² + 6x + 8 to represent the area of the floor of a room. If the decides that the length of the room will be represented by (x + 4), what will the width of the room be in terms of x ?
Solution:
Given length of the room = x + 4
Area of the room = x² + 6x + 8
Length × breadth = x² + 6x + 8

Question 8.
Find the missing term: y² + (-) x + 56 = (y + 7)(y + -)
Solution:
We have (x + a) (x + b) = x² + (a + b)x + ab
56 = 7 × 8 .
∴ y² + (7 + 8)x + 56 = (y + 7)(y + 8)

Question 9.
Factorise: 16p⁴ – 1
Solution:
16p⁴ – 1 = 2⁴p⁴ – 1 = (2²)²(p²)² – 1²
Comparing with a² – b² = (a + b)(a – b) where a = 2²p² and b = 1
∴ (2²p²)² – 1² = (2²p² + 1) (2²p² – 1) = (4p² + 1) (4p² – 1)
∴ 16p⁴ – 1 = (4p² + 1)(4p² – 1)(4p² + 1)(2²p² – 1²)
= (4p² + 1) [(2p)²– 1²] = (4p² + 1) (2p + 1)(2p – 1)
[∵ using a² – b² = (a + b) (a – b)]
∴ 16p⁴ – 1 = (4psup>2 + 1)(2p + 1)(2p – 1)

Question 10.
Factorise : x⁶ – 64y³
Solution:
x⁶ – 64y³ = (x²)³ – 4³y³ = (x²)³ – (4y)³
This is of the form a³ – b³ with a = x², b = 4y
a³ – b³ = (a – b)(a² + ab + b²)
(x²)³ – (4y)³ = (x² – 4y) [(x²)² + (x²)(4y) + (4y)²]
= (x² – 4y) [x⁴ + 4x²y + 16y²]
∴ x⁶ – 64y³ = (x² – 4y) [x⁴ + 4x²y + 16y²]