Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.1

Students can Download Maths Chapter 4 Geometry Ex 4.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.1

Question 1.
From the figure given, prove that ∆ABC ~ ∆DEF.

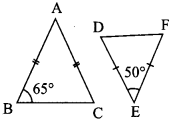
Solution:
From the ∆ABC,
AB = AC
It is an isosceles triangle
Angles opposite to equal sides are equal
∴ ∠B = ∠C = 65°
∴ ∠B + ∠C = 65° + 65°
= 130°
We know that .sum of three angles is a triangle = 180°
∠A + ∠B + ∠C = 180°
∠A + 130° = 180°
∠A = 180°-130°
∠A = 50°
From ∆DEF, ∠D = 50°
∴ Sum of Remaining angles = 180° – 50° = 130°
DE = FD
∴ ∠D = ∠F
From ∆ABC and ∆DEF

∠A = ∠D = 50°
∠B = ∠E = 65°
∠C = ∠F = 65°
∴ By AAA criteria ∆DEF ~ ∆ABC

Question 2.
Prove that ∆GUM ~ ∆ BOX from the given figure.

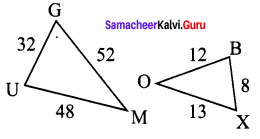
Solution:


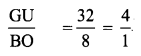
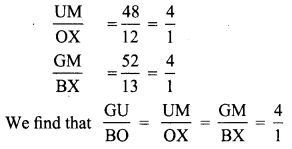
That is their corresponding sides are proportional.
∴ By SSS similarity ∆GUM ~ ∆BOX.

Question 3.
In the given figure YH ||TE Prove that ∆WHY ~ ∆WET and also find HE and TE.

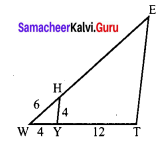
Solution:

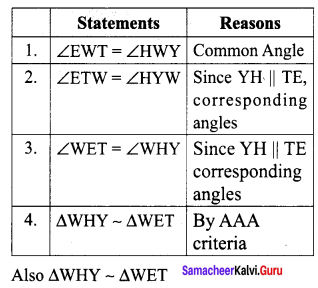
Question 4.
In the given figure, if ∆EAT ~ ∆BUN find the measure of all angles.

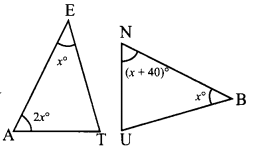
Solution:
Given ∆EAT ≡ ∆BUN
∴ Corresponding angles are equal
∴ ∠E = ∠B ..(1)
∠A = ∠U ..(2)
∠T = ∠N ..(3)
∠E = x°
∠A = 2x°
Sum of three angles of a triangle = 180°
In ∆EAT, x + 2x + ∠T = 180°
∠T = 180° – (x° + 2x° )
∠T = 180°- 3x° …(4)
Also in ∆BUN
(x + 40)° + + ∠U = 180°
x + 40° + x + ∠U = 180°
2x° + 40° + ∠U = 180°
∠U = 180° – 2x – 40°
= 140° – 2x°
Now by (2)
∠A = ∠U
2x = 140° – 2x
2x + 2x = 140°
4x = 140°

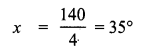
∠A = 2x° = 2 × 35° = 70°
∠N = x + 40°
= 35° + 40° = 75°
∴ ∠T = ∠N = 75°
∠E = ∠B = 35°
∠A = ∠U = 70°

Question 5.
From the given figure, UB || AT and CU ≡ CB Prove that ∆CUB ~ ∆CAT and hence ∆CAT is isosceles.

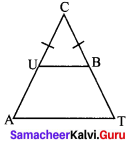
Solution:

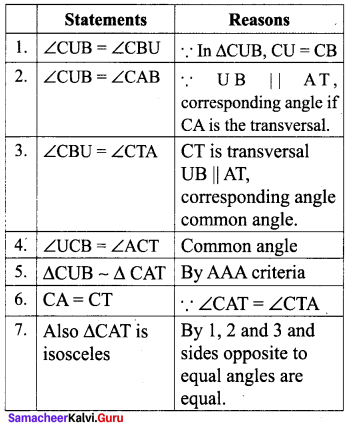
Question 6.
In the figure, ∠CIP ≡ ∠COP and ∠HIP ≡ ∠HOP. Prove that IP ≡ OP.

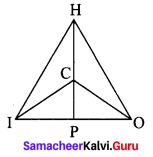
Solution:

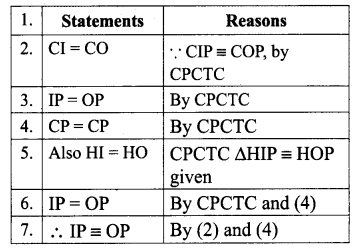
Question 7.
In the given triangle, AC ≡ AD and ∠CBD ≡ ∠DEC. Prove that ∆BCF ≡ ∆EDF.

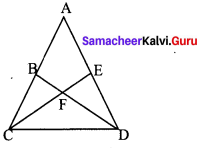
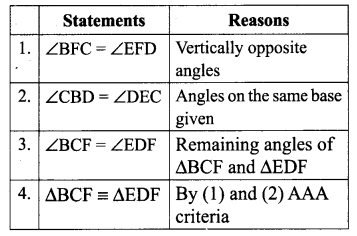
Solution:

Question 8.
In the given figure, ∆ BCD is isosceles with base BD and ∠BAE ≡ ∠DEA. Prove that AB ≡ ED .

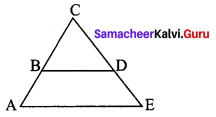
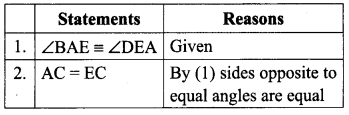
Solution:

Question 9.
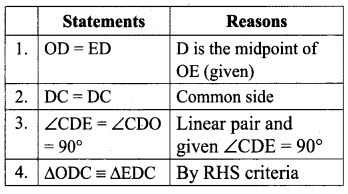
In the given figure, D is the midpoint of OE and ∠CDE = 90°. Prove that ∆ODC ≡ ∆EDC.

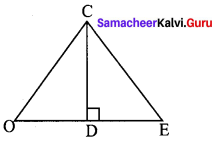
Solution:

Question 10.
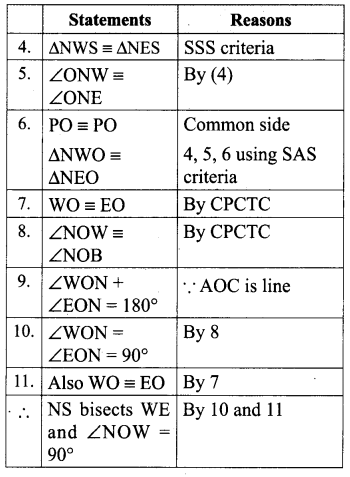
In the figure, if SW ≡ SE and ∠NWO ≡ ∠NEO. then, prove that NS bisects WE and ∠NOW = 90°

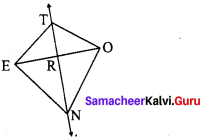
Proof:

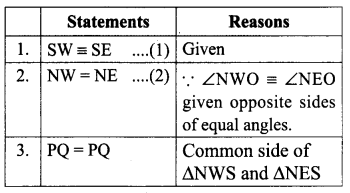
Question 11.
Is ∆PRQ ≡ ∆QSP ? Why ?

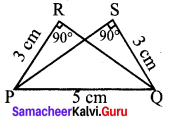
Solution:
In ∠PRQ = ∠PSQ = 90° given
PR = QS = 3 cm given
PQ = PQ = 5 cm common
It satisfies RHS criteria
∴ ∆PRQ congruent to ∆QSP.

Question 12.
Fill in the blanks with the most correct term from the given list.
(in proportion, similar, corresponding, congruent shape, area, equal)
Statements Reasons

Question 1.
Corresponding sides of similar triangles are ___.
Solution:
in proportion

Question 2.
Similar triangles have the same ___ but not necessarily the same size.
Solution:
shape

Question 3.
In similar triangles, ___ sides are opposite to equal angles.
Solution:
equal

Question 4.
The symbol ~ is used to represent ___ triangles.
Solution:
congruent

Question 5.
The symbol ~ is used to represent ____ triangles.
Solution:
similar

Objective Type Questions

Question 13.
Two similar triangles will always have ___ angles
(A) acute
(B) obtuse
(C) right
(D) matching
Solution:
(D) matching

Question 14.
If in triangles PQR and XYZ, \(\frac{P Q}{X Y}=\frac{Q R}{Z X}\) then they will be similar if
Solution:
(C) Q = ∠X

Question 15.
A flag pole 15 cm high casts a shadow of 3 m at 10 a.m. The shadow cast by a building at the same time is 18.6 m. The height of the building is
(A) 90 m
(B) 91 m
(C) 92 m
(D) 93 m
Solution:
(D) 93 m

Question 16.
If ∆ABC ~ ∆PQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Solution:
(A) 50°

Question 17.
In the figure, which of the following statements is true?
(A) AB = BD
(B) BD < CD
(C) AC = CD
(D) BC = CD

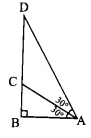
Solution:
(C) AC = CD