Students can Download Maths Chapter 4 Geometry Ex 4.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.2
Miscellaneous Practice Problems
Question 1.
In the given figure, find PT given that l1 || l2
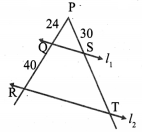
Solution:
Given that l1 || l2
∴ In ∆PQS and ∆PRT
∠P is common
∠Q = ∠R [∵ PR is the transversal for l1 and l2 corresponding angles]
∠S = ∠T [∵ corresponding angles]
∴ ∆PQS ~ ∆PRT [∵ By AAA congruency]
In similar triangles, corresponding angles are proportional.
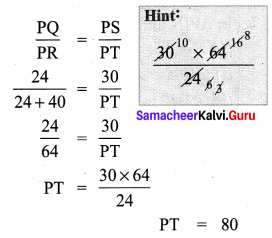
Question 2.
From the diagram, prove that ∆SUN ~ ∆RAY
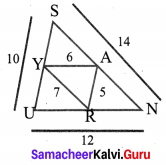
Proof:
From the ∆SUN and ∆RAY
SU = 10;
UN = 12;
SN = 14;
RA = 5,
AY = 6;
RY = 7
We have


Question 3.
The height of a tower is measured by a mirror on the ground by which the top of the tower’s reflection is seen. Find the height of the tower.
Solution:
The image and its reflection make similar shapes
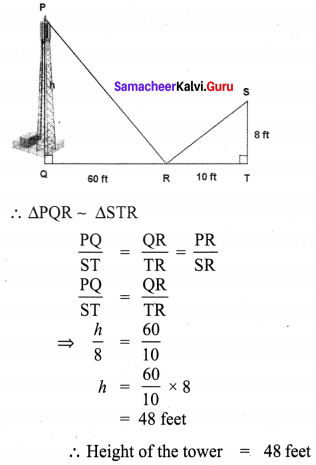
![]()
Question 4.
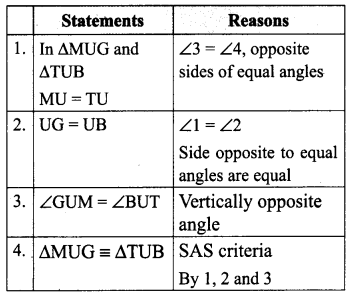
In the figure, given that ∠1 = ∠2 and ∠3 ≡ ∠4 Prove that ∆MUG ≡ ∆ TUB.
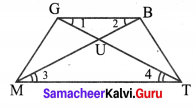
Proof:
Question 5.
If ∆WAR ≡ ∆MOB, name the additional pair of corresponding parts. Name the criterion used by you.
Solution:

Given ∆WAR ≡ ∆MOB
∠RWA ≡ ∠BMO [∵ sum of three angles of a triangle are 180°]
∴ Criteria used here is angle sum property of triangles.
Question 6.
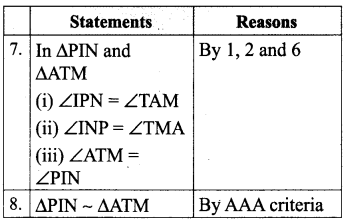
In the figure, ∠TMA ≡ ∠IAM and ∠TAM ≡ ∠IMA. P is the midpoint of MI and N is the midpoint of AI. Prove that ∆ PIN ~ ∆ ATM.
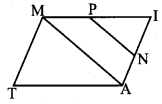
Solution:

![]()
Question 7.
In the figure, if ∠FEG = ∠1 then, prove that DG2 = DE.DF.
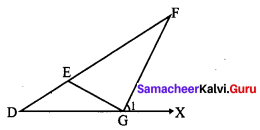
Proof:
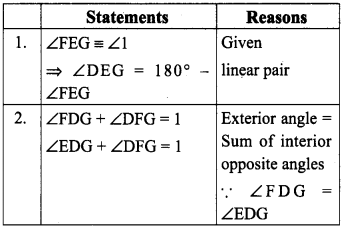
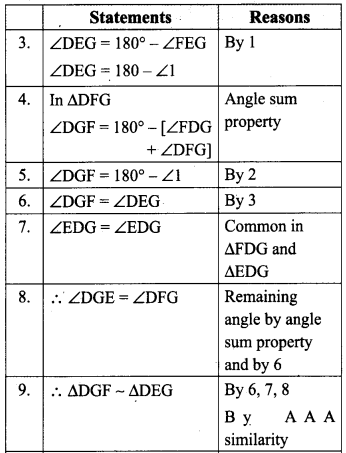
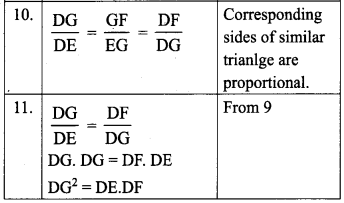
Question 8.
In the figure, ∠TEN ≡ ∠TON = 90° and TO = TE. Prove that ∠ORN ≡ ∠ERN
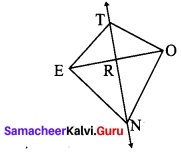
Solution:

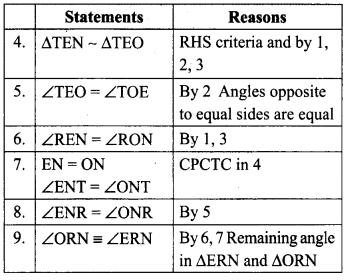
Question 9.
In the figure, PQ ≡ TS, Q is the midpoint of PR, S is the midpoint TR and ∠POU ≡ ∠TSU. Prove that QU ≡ SU.

Proof:

![]()
Question 10.
In the figure ∆TOP ≡ ∆ARM . Explain why?
Solution:
In ∆TOP and ∆ARM
OP = RM given
∠TOP = ∠ARM = 90°
given ∠OTP = ∠RAM
given ∠OPT = ∠RMA Remaining angle, by angle sum property.
∴ By ASA criteria we can say that ∆TOP ≡ ∆ARM