You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.11
Question 1.
Solve, using the method of substitution
(i) 2x – 3y = 7; 5x + y = 9
(ii) 1.5x + 0.1y = 6.2; 3x – 0.4y = 11.2
(iii) 10% of x + 20% of y = 24; 3x – y = 20
(iv) \(\sqrt{2} x-\sqrt{3} y=1 ; \sqrt{3} x-\sqrt{8} y=0\)
Solution:
(i) 2x – 3y = 7 ………….. (1)
5x + y = 9 ………….. (2)
Step (1)
From the equation (2)
5x+ y = 9
y = -5x + 9
Step (2)
substitute (3) in (1)
2x – 3(-5x + 9) = 7
2x + 15x – 27 = 7
17x = 7 + 27
17x = 34
x = \(\frac{34}{17}\) = 2; x = 2
Step (3)
substitute x = 2 in (3)
y = – 5(2) + 9 = -10 + 9 = -1
Solution: x = 2; y = -1
(ii) 1.5x + 0.1y = 6.2 …………. (1)
3x – 0.1y = 11.2 ………….. (2)
Multiply (1 ) x 10 15x + y = 62 ……….(1)
(2) × 10 ⇒ 30x – 4y = 112 …………. (4)
Step (1)
From equation (3)
15x + y = 62
y = -15x + 62 …………. (5)
Step (2)
substitute (5) in (4)
30x – 4 (-15x + 62) = 112
30x + 60x – 248 = 112
90x = 112 + 248
90x = 360
x = \(\frac{360}{90}\)
x = 4
Step (3)
substitute x = 4 in (5)
y = -15(4) + 62
= -60 + 62
y = 2
Solution: x = 4; y = 2
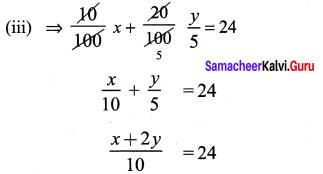
x + 2y = 240 ………. (1)
3 x – y =20 ……….. (2)
Step (1)
From equation (2)
3x – y = 20
-y = 20 – 3x
y = 3x – 20 — (3)
Step (2)
substitute (3) in (1)
x + 2(3x – 20) = 240
x + 6x – 40 = 240
7x = 240 + 40
x = \(\frac{280}{7}\)
x = 40
Step (3)
substitute x = 40 in (3)
y = 3 (40) – 20
= 120 – 20 = 100
Solution : x = 40 and y = 100
(iv) \(\sqrt{2} x-\sqrt{3} y\) = 1 ………… (1)
\(\sqrt{3} x-\sqrt{8} y\) = 0 ……….. (2)
Step (1)
From the equation (2)


Solution: x = \(\sqrt{8}\) and y = \(\sqrt{3}\)
Question 2.
Raman’s age is three times the sum of the ages of his two sons. After 5 years his age will be twice the sum of the ages of his two sons. Find the age of Raman.
Solution:
Let Raman’s age = x
Let the sum of his two sons age = y
now x = 3y ⇒ x – 3y = 0 ……… (1)
After 5 years,
Step (3)
x + 5 = 2(y + 10)
x + 5 = 2y + 20
x – 2y = 20 – 5
x – 2y = 15
Step (1)
From equation (1) x = 3y
Step (2)
Substitute x = 3y in (2)
3y – 2y = 15
y = 15
Step (3)
Substitute y = 15 in (1)
x = 3y = 3 × 15
x = 45
∴ Raman’s age is 45 years.
![]()
Question 3.
The middle digit of a number between 100 and 1000 is zero and the sum of the other digit is 13. If the digits are reversed, the number so formed exceeds the original number by 495. Find the number.
Solution:
Let the number be x0y
x + y = 13 …………….. (1)
If the digits are reversed the number so formed is y0x
x0y = 100x + 10 × 0 + 1 × y
y0x = 100y + 10 × 0 + 1 × x
100y + x – (100x + y) = 495
100y + x – 100x – y = 495
-99x + 99y = 495 ………….. (2)
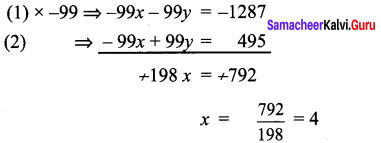
Substitute x = 4 in (1)
4 + y = 13 = 13 – 4 = 9
The number is 409.