You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.13
Question 1.
Solve by cross-multiplication method
(i) 8x – 3y = 12; 5x = 2y + 7
(ii) 6x + 7y – 11 = 0; 5x + 2y = 13
(iii) \(\frac{2}{x}+\frac{3}{y}=5 ; \frac{3}{x}-\frac{1}{y}+9=0\)
Solution:
(i) 8x – 3y = 12 ……….. (1)
5x – 2y = 7 ………… (2)
8x – 3y – 12 = 0
5x – 2y – 7 = 0
For cross multiplication method, we write the co-efficients as
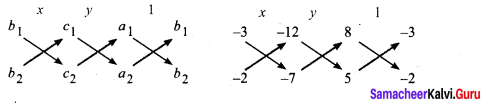
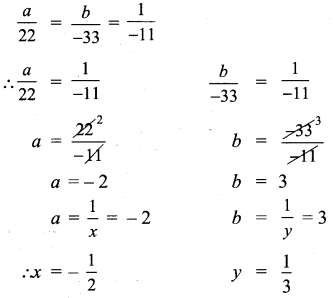
(ii) 6x + 7y – 11 = 0
5x + 2y – 13 = 0
For cross multiplication method, we write the co-efficients as
∴ Solutions: x = 3; y = -1
(iii) \(\frac{2}{x}+\frac{3}{y}\) – 5 = 0 ……….. (1)
\(\frac{3}{x}-\frac{1}{y}\) + 9 = 0 ………… (2)
In (1), (2) Put \(\frac{1}{x}\) = a, \(\frac{1}{y}\) = b
(1) ⇒ 2a + 3b – 5 = 0
(2) ⇒ 3a – b + 9 = 0
For cross multiplication method, we write the co-efficients as
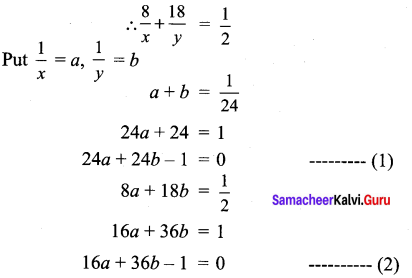
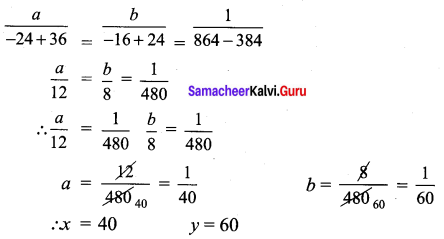
Solution: x = \(-\frac{1}{2}\); y = \(\frac{1}{3}\)
![]()
Question 2.
Akshaya has 2 rupee coins and 5 rupee coins in her purse. If in all she has 80 coins totalling ₹ 220, how many coins of each kind does she have.
Solution:
Let the number of 2 rupee coins be x
Let the number of 5 rupee coins be y
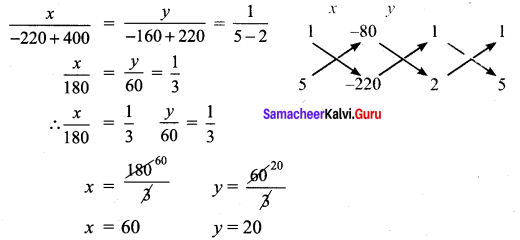
x + y = 80
2x + 5y = 220
x + y – 80 = 0
2x + 5y – 220 = 0
For cross multiplication method, we write the co-efficients as
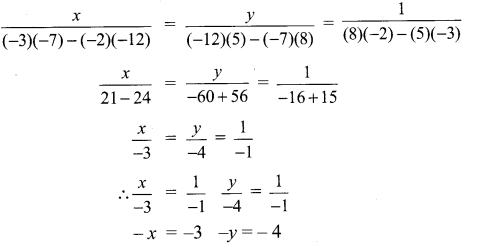
∴ No. of 2 rupee coins = 60
No. of 5 rupee coins = 20
Question 3.
It takes 24 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for 8 hours and the pipe of the smaller diameter is used for 18 hours. Only half of the pool is filled. How long would each pipe take to fill the swimming pool.
Solution:
Let the time taken by the larger pipe be x hours and Set the time taken by the smaller pipe be y hours.
∴ \(\frac{1}{x}+\frac{1}{y}=\frac{1}{24}\)
In 1 hour the larger pipe can fill it = \(\frac{1}{x}\)
In 1 hour the smaller pipe can fill it \(\frac{1}{y}\)

For cross multiplication method, we write the co-efficients as
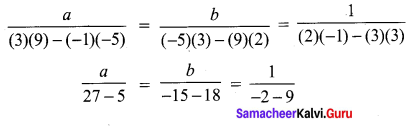
∴ To fill the full tank the larger pipe takes 40hrs
To fill the full tank the smaller pipe takes 60hrs