You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.4
9th Maths Algebra Exercise 3.4 Question 1.
Expand the following :
(i) (2x + 3y + 4z)2
(ii) (-p + 2q + 3r)2
(iii) (2p + 3)(2p – 4)(2p – 5)
(iv) (3a + 1)(3a – 2)(3a + 4)
Solution:
(i) (2x + 3y + 4z)2
(a + b + c)2 ≡ a2 + b2 + c2 + 2ab + 2bc + 2ca
∴ (2x + 3y + 4z)2 = (2x)2 + (3y)2 + (4z)2 + 2 (2x) (3y) + 2 (3y) (4z) + 2 (4z) (2x)
= 4x2 + 9y2 + 16z2 + 12xy + 24yz + 16zx
(ii) (-p + 2q + 3r)2
(a + b + c)2 ≡ a2 + b2 + c2 + 2ab + 2bc + 2ca
(-p + 2q + 3r)2 = (-p)2 + (2q)2 + (3r)2 + 2(-p) (2q) + 2(2q) (3r) + 2 (-p) (3r)
= p2 + 4q2 + 9r2 – 4pq +12qr – 6rp
(iii) (2p + 3)(2p – 4)(2p – 5)
(x + a) (x + b) (x + c) ≡ x3 + (a + b + c) x2 + (ab + be + ca) x + abc
(2p + 3)(2p – 4)(2p – 5) = (2p)3 + (3 – 4 – 5) (2p)2 + [(3 × – 4)2 + (-4 × -5) + (-5 × 3)] 2p + 3 × – 4 × – 5
= 8p3 + (-6) (4p2) + [-12 + 20 + (-15)] 2p + 60
= 8p3 – 24p2 + (-7)2p + 60
(2p + 3)(2p – 4)(2p – 5) = 8p3 – 24p2 – 14p + 60
(iv) (3a + 1)(3a – 2)(3a + 4)
(x + a) (x + b) (x + c) ≡ x3 + (a + b + c) x2 + (ab + bc + ca) x + abc
(3a + 1)(3a – 2)(3a + 4) = (3a)3 + (1 – 2 + 4) (3a)2 + [1 × (- 2) + (-2 × 4) + 4 × 1] (3a) + 1 × -2 × 4
= 27a3 + 3 (9a2) + (-2 – 8 + 4)3a – 8
= 27a3 + 27a2 – 8a – 8
9th Maths Exercise 3.4 Question 2.
Using algebraic identity, find the coefficients of x2, x and constant term without actual expansion.
(i) (x + 5)(x + 6)(x + 7)
(ii) (2x + 3)(2x – 5)(2x – 6)
Solution:
(i) (x + 5)(x + 6)(x + 7)
(x + a) (x + b) (x + c) ≡ x3 + (a + b + c) x2 + (ab + bc + ca) x + abc
Co-efficient of x2 = a + b + c = 5 + 6 + 7 = 18
Co-efficient of x2 = ab + bc + ca = (5 × 6) + (6 × 7) + (7 × 5)
= 30 + 42 + 35 = 107
Constant term = abc = 5 × 6 × 7
Co-efficient of constant term = 210
(ii) (2x + 3)(2x – 5)(2x — 6)
∴ Co-efficient of x2 = 4 (a + b + c) = 4 (3 + (-5) + (-6))
= 4 × (-8) = -32
Co-efficient of x = 2 (ab + bc + ca)
= 2 [3 × (-5) + (-5) (-6) + (-6) (3)]
= 2[-15 + 30- 18] = 2 × (-3) = -6
Constant term = abc = 3 × (-5) × (-6) = 90
Class 9 Maths Exercise 3.4 Solutions Question 3.
If (x + a)(x + b)(x + c) = x3 + 14x2 + 59x + 70, find the value of
(i) a + b + c
(ii) \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
(iii) a2 + b2 + c2
(iv) \(\frac{a}{b c}+\frac{b}{a c}+\frac{c}{a b}\)
Solution:
(x + a)(x + b)(x + c) = x3 + 14x2 + 59x + 70 …………….. (1)
(x + a) (x + b) (x + c) ≡ x3 + (a + b + c) x2 + (ab + bc + ca) x + abc …………. (2)
(i) Comparing (1) & (2)
We get, a + b + c = 14
(ii) \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{b c+a c+a b}{a b c}=\frac{59}{70}\)
(iii) (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
= 142 – 2 (59) = 196 – 118 = 78
(iv) \(\frac{a}{b c}+\frac{b}{a c}+\frac{c}{a b}=\frac{a^{2}+b^{2}+c^{2}}{a b c}=\frac{78}{70}=\frac{39}{35}\)
9th Class Maths Exercise 3.4 Solution Question 4.
Expand
(i) (3a – 4b)3
(ii) (x + \(\frac{1}{y}\))3
Solution:
(i) (3a – 4b)3 We know that
(x – y)3 = x3 – 3x2y + 3xy2 – y3
(3a-4b)3 = (3a)3 – 3 (3a)2 (4b) + 3 (3a) (4b)2 – (4b)3
= 27a3 – 108a2b + 144 ab2 – 64b3
(ii) (x + \(\frac{1}{y}\))3
(x + y)3 ≡ x3 + 3x2y + 3xy2 + y3
\(\left(x+\frac{1}{y}\right)^{3}=x^{3}+\frac{3 x^{2}}{y}+\frac{3 x}{y^{2}}+\frac{1}{y^{3}}\)
Exercise 3.4 Class 9 Maths Solution Question 5.
Evaluate the following by using identities:
(i) 983
(ii) 10013
Solution:
(i) 982 = (100 – 2)3
(a – b)3 ≡ a3 – 3a2b + 3ab2 – b3
983 = (100 – 2)3 = 1003 – 3 × 1002 × + 3 × 100 × 22 – 23
= 1000000 – 3 × 10000 × 2 + 300 × 4 – 8
= 1000000 – 60000 + 1200 – 8 = 1001200 – 60008 = 941192
(ii) 10013 = (1000 + 1)3
(a + b)3 ≡ a3 + 3a2b + 3ab2 + b3
(1000 + 1)3 = 10003 + 3(10002) × 1 + 3 × 1000 × 12 + 13
= 1000,000,000 + 3,000,000 + 3000 + 1 = 1,003,003,001
9th Standard Maths Exercise 3.4 Question 6.
If (x + y + z) = 9 and (xy + yz + zx) = 26 then find the value of x2 + y2 + z2.
Solution:
(x + y + z) = 9 and(xy + yz + zx) = 26
x2 + y2 + z2 = (x + y + z)2 – 2 (xy + yz + zx)
= 92 – 2 × 26 = 81 – 52 = 29
9th Class Math Exercise 3.4 Solution Question 7.
Find 27a3 + 64b3, if 3a + 4b = 10 and ab = 2.
Solution:
3a + 4b = 10, ab = 2
(3a + 4b)3 = (3a)3 + 3 (3a)2 (4b) + 3 (3a) (4b)2 + (4b)3
(27a3 + 64b3) = (3a + 4b)3 – 3 (3a) (4b) (3a + 4b)
∵ x3 + y3 = (x + y)3 – 3xy – (x + y)
= 103 – 36 ab (10)= 1000 – 36 × 2 × 10
= 1000 – 720 = 280
Maths Class 9 Chapter 3 Exercise 3.4 Question 8.
Find x3 – y3, if x – y = 5 and xy = 14.
Solution:
x – y = 5, xy = 14
x3 – y3 = (x – y)3 + 3xy (x – y) = 53 + 3 × 14 × 5
= 125 + 210 = 335
Maths Exercise 3.4 Class 9 Question 9.
If a + \(\frac{1}{a}\) = 6, then find the value of a3 + \(\frac{1}{a^{3}}\)
Solution:
a3 + b3 = (a + b)3 – 3ab (a + b)
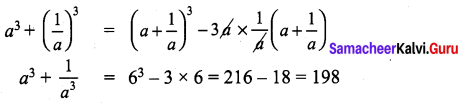
9th Class Math Ex 3.4 Solution Question 10.
If x2 + \(\frac{1}{x^{2}}\) = 23, then find the value of x + \(\frac{1}{x}\) and x3 + \(\frac{1}{x^{3}}\)
Solution:
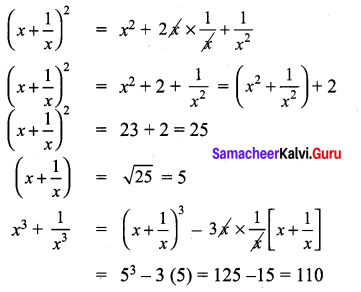
9th Class Math, Exercise 3.4 Solution Question 11.
If (y – \(\frac{1}{y}\))3 = 27, then find the value of y3 – \(\frac{1}{y^{3}}\)
Solution:
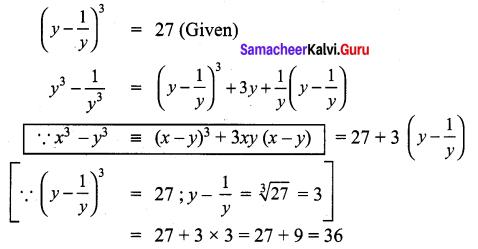
9th Class Math Chapter 3 Exercise 3.4 Question 12.
Simplify : (i) (2a + 36 + 4c)(4a2 + 9b2 + 16c2 – 6ab – 12bc – 12bc – 8ca)
(ii) (x – 2y + 3z) (x2 + 4y2 + 9z2 + 2xy + 6yz – 3xz)
Solution:
(i) (2a + 36 + 4c)(4a2 + 9b2 + 16c2 – 6ab – 12bc – 12bc – 8ca)
We know that
(a + b + c) (a2 + b2 + c2 – ab – bc – ca) = a3 + b3 + c3 × 3 abc
∴ (2a + 36 + 4c) (4a2 + 9b2 + 16 c2 – 6 ab – 12 bc – 8 ca)
= (2a)3 + (3b)3 + (4c)3 – 3 × 2a × 36 × 4c
= 8a3 + 27b3 + 64c3 – 72 abc
(ii) (x – 2,y + 3z) (x2 + 4y2 + 9z2 + 2xy + 6yz – 3xz)
(a + b + c) (a2 + b2 + c2 – ab – bc – ca) = a3 + b3 + c3 – 3abc .
∴ (x – 2y + 3z) (x2 + 4y2 + 9z2 + 2xy + 6yz – 3xz)
= x3 + (-2y)3 + (3z)3 – 3 × x × (-2y) (3z)
= x3 – 8y3 + 27z3 + 18 xyz
9 Class Math 3.4 Solution Question 13.
By using identity evaluate the following:
(i) 73 – 103 + 33
(ii) 1 + \(\frac{1}{8}-\frac{27}{8}\)
Solution:
(i) 73 – 103 + 33
(a + b + c) (a2 + b2 + c2 – ab – bc – ca) = a3 + b3 + c3 – 3 abc
If a + b + c = 0, then a3 + b3 + c3 = 3 abc
∴ 7 – 10 + 3 = 0
⇒ 73 – 103 + 33 = 3 × 7 × – 10 × 3
= 9 × -70 = -630
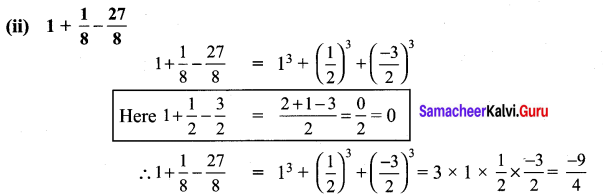
Ex 3.4 Class 9 Maths Solutions Question 14.
If 2x – 3y – 4z = 0, then find 8x3 – 27y3 – 64z3.
Solution:
If 2x – 3y – 4z = 0 then 8x3 – 27y3 – 64z3 = ?
If x + y + z = 0 then x3 + y3 + z3 = 3xyz
8x3 – 21 y3 – 64z3 = (2x)3 + (-3y)3 + (-4z)3
= 3 × 2x × -3y × – 4z = 72 xyz