You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.7
9th Maths Exercise 3.7 Question 1.
Find the quotient and remainder of the following.
(i) (4x3 + 6x2 – 23x + 18) ÷ (x + 3)
(ii) (8y3 – 16y2 + 16y -15) ÷ (2y – 1)
(iii) (8x3 – 1) ÷ (2x – 1)
(iv) (-18z + 14z2 + 24z3 + 18) ÷ (3z + 4)
Solution:
(i) (4x3 + 6x2 – 23x + 18) ÷ (x + 3)
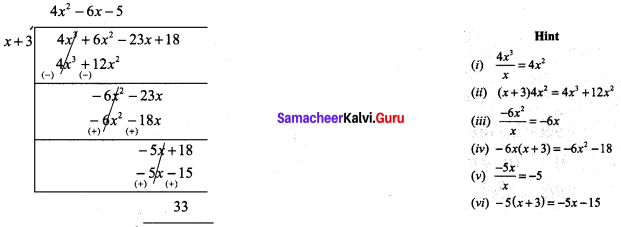
Quotient = 4x2 – 6x – 5
Remainder = 33
(ii) (8y3 – 16y2 + 16y -15) ÷ (2y – 1)

Quotient = 4y2 – 6y + 5
Remainder = -10
(iii) (8x3 – 1) ÷ (2x – 1)

Quotient = 4x2 + 2x + 1
Remainder = 0
(iv) (-18z + 14z2 + 24z3 + 18) ÷ (3z + 4)

Quotient = 8z2 – 6z + 2
Remainder = 10
9th Maths Algebra Exercise 3.7 Question 2.
The area of rectangle is x2 + 7x + 12. If its breadth is (x + 3), then find its length.
Solution:
Area of a rectangle = x2 + 7x + 12
Its breadth = x + 3
Area = breadth × length
x2 + 7x + 12 = (x + 3) × length
∴ Length = (x2 + 7x + 12) ÷ (x + 3)

Quotient = x + 4; Remainder = 0;
∴ Length = x + 4
Samacheer Kalvi 9th Maths Question 3.
The base of a parallelogram is (5x + 4). Find its height, if the area is 25x2 – 16.
Solution:
The base of a parallelogram is (5x + 4)
Area = 25x2 – 16
Area = b × h = 25x2 – 16
base = 5x + 4
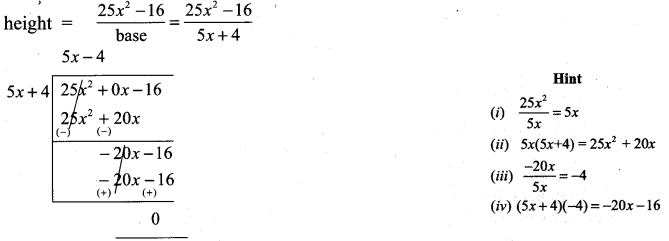
∴ height of the parallelogram = 5x – 4.
9th Maths Samacheer Kalvi Question 4.
The sum of (x + 5) observations is (x3 + 125). Find the mean of the observations.
Solution:
The sum of (x + 5) observations is (x3 + 125)


Quotient = x2 – 5x + 25
Remainder = 0
∴ Mean of the observations = x2 – 5x + 25
![]()
Samacheerkalvi.Guru 9th Maths Question 5.
Find the quotient and remainder for the following using synthetic division:
(i) (x3 + x2 – 7x – 3) ÷ (x – 3)
(ii) (x3 + 2x2 – x – 4) ÷ (x + 2)
(iii) (3x3 – 2x2 + 7x – 5) ÷ (x + 3)
(iv) (8x4 – 2x2 + 6x + 5) ÷ (4x + 1)
Solution:
(i) (x3 + x2 – 7x – 3) ÷ (x – 3)
Let p (x) = x3 + x2 – 7x – 3
q (x) = x – 3 To find the zero of x – 3
p(x) in standard form ((i.e.) descending order)
x3 + x2 – 7x – 3
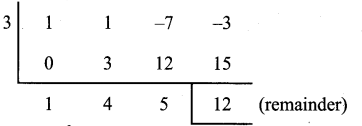
Quotient is x2 + 4x + 5
Remainder is 12
(ii) (x3 + 2x2 – x – 4) + (x + 2)
p (x) = x3 + 2x2 – x – 4
Co-efficients are 1 2 -1 – 4
To find zero of x + 2, put x + 2 = 0; x = -2
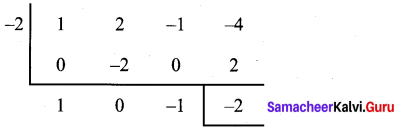
∴ Quotient is x2 – 1
Remainder is -2
(iii) (3x3 – 2x2 + 7x – 5) ÷ (x + 3)
To find zero of the divisor (x + 3), put x + 3 = 0; ∴ x = – 3
Dividend in Standard form 3x3 – 2x2 + 7x – 5
Co-efficients are 3 -2 7 – 5
Synthetic Division
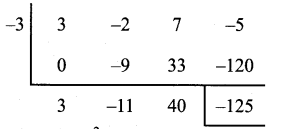
Quotient is 3x2 – 11x + 40
Remainder is -125
(iv) (8x4 – 2x2 + 6x + 5) ÷ (4x + 1)
To find zero of the divisor 4x + 1, put 4x + 1 = 0 ; 4x = -1; x = \(-\frac{1}{4}\)
Dividend in Standard form 8x4 + 0x3 – 2x2 + 6x + 5
Co-efficients are 8 0 -2 6 5
Synthetic Division

Samacheer Kalvi Maths 9th Question 6.
If the quotient obtained on dividing (8x4 – 2x2 + 6x – 7) by (2x + 1) is (4x3 + px2 -qx + 3), then find p, q and also the remainder.
Solution:
Let p (x) = 8x4 – 2x2 + 6x – 7
Standard form = 8x4 + 0x3 – 2x2 + 6x – 7
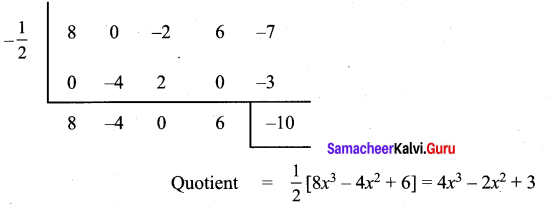
Quotient 4x3 – 2x2 + 3 is compared with the given quotient 4x3 + px2 – qx + 3
Co-efficients of x2 is p = – 2
Co-efficients of x is q = 0
Remainder is – 10
9th Maths Algebra Question 7.
If the quotient obtained on dividing 3x3 + 11x2 + 34x + 106 by x – 3 is 3x2 + ax + b, then find a, b and also the remainder.
Solution:
Let p (x) = 3x3 + 11x2 + 34x + 106
p (x) in standard form
Co-efficients are 3 11 34 106
q(x) = x – 3, its zero x = 3
Synthetic division
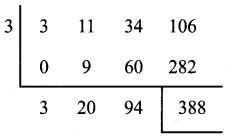
Quotient is 3x2 + 20x + 94, it is compared with the given quotient 3x2 + ax + b
Co-efficient of x is a = 20
Constant term is b = 94
Remainder r = 388