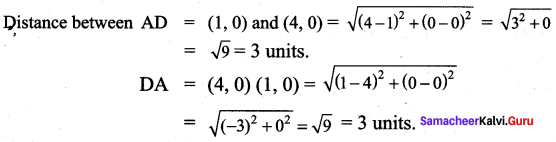Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions

Exercise 5.1

Question 1.
State whether the following statements are true/false.
(i) (5, 7) is a point in the IV quadrant.
(ii) (-2, -7) is a point in the III quadrant.
(iii) (8, -7) lies below the x-axis.
(iv) (-2, 3) lies in the II quadrant.
(v) For any point on the x-axis its y-coordinate is zero.
Solution:
(i) False
(ii) True
(iii) True
(iv) True
(v) True

Question 2.
Locate the points
(i) (3, 5) and (5, 3)
(ii) (-2, -5) and (-5, -2) in the rectangular coordinate system.
Solution:

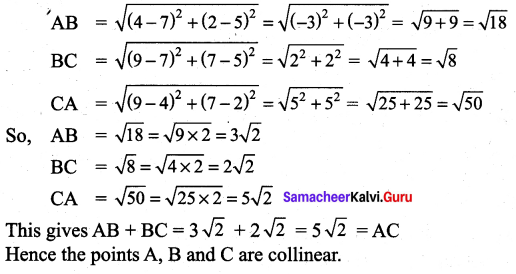
Question 3.
In which quadrant does the following points lie?
(i) (5, 2)
(ii) (-5, -8)
(iii) (-7, 1)
(iv) (8, -3)
Solution:
(i) I quadrant
(ii) III quadrant
(iii) II quadrant
(iv) IV quadrant.

Question 4.
Write down the ordinate of the following points.
(i) (7, 5)
(ii) (2, 9)
(iii) (-5, 8)
(iv) (7, -4)
Solution:
(i) 5
(ii) 9
(iii) 8
(iv) -4 (ordinate is the y-coordinate)

Exercise 5.2

Question 1.
Find the distance between the following pairs of points.
(i) (-4, 0) and (3, 0)
(ii) (-7, 2) and (5, 2)
Solution:
(i) The points (-4, 0) and (3, 0) lie on the x-axis. Hence,

(ii) The points (5,2) and (-7,2) lie on a line parallel to the x-axis. Hence the distance

Question 2.
Show that the three points (4, 2), (7, 5) and (9, 7) lie on a straight line.
Solution:
Let the points be A(4, 2), B(7, 5) and C(9, 7). By the distance formula.

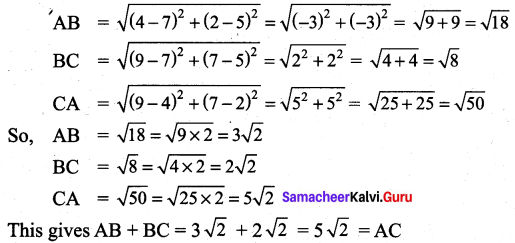
Hence the points A, B and C are collinear.

Question 3.
Determine whether the points are vertices of a right triangle A(-3, -4), B(2, 6) and C (-6, 10).
Solution:

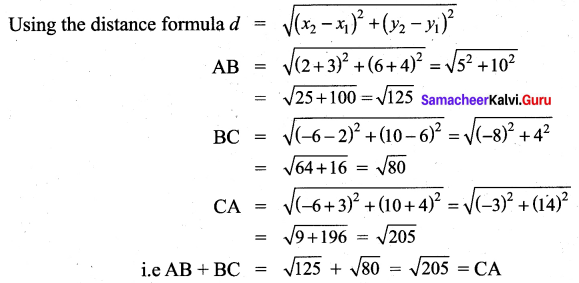
Hence ABC is a right angled triangle since the square of one side is equal to sum of the squares of the other two sides.

Question 4.
Show that the points (a, a), (-a, -a) and (\(-a \sqrt{3}, a \sqrt{3}\)) form an equilateral triangle.
Solution:
Let the points be represented by A (a, a), B(-a, -a) and C(\(-a \sqrt{3}, a \sqrt{3}\)) using the distance formula.

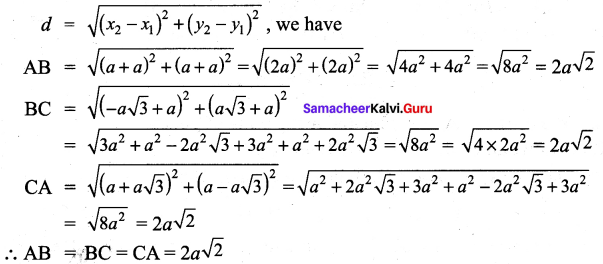
Since all the sides are equal the points form an equilateral triangle.

Question 5.
Prove that the points (-7, -3), (5, 10), (15, 8) and (3, -5) taken in order are the corners of a parallelogram.
Solution:
Let A, B, C and D represent the points (-7, -3), (5, 10), (15, 8) and (3, -5) respectively.

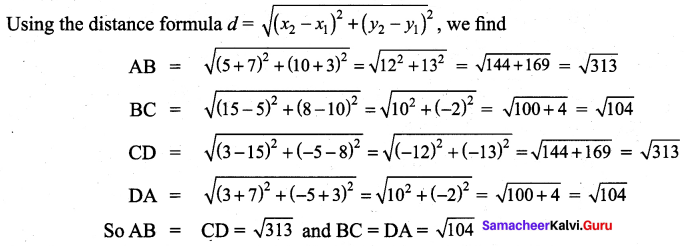
i.e. The opposite sides are equal. Hence ABCD is a parallelogram.

Question 6.
Show that the following points A (3, 1) B(6, 4) and C(8, 6) lies on a straight line.
Solution:
Using the distance formula, we have

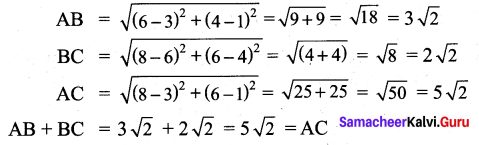
Therefore the points lie on a straight line.

Question 7.
If the distance between the points (5, -2), (1, a) is 5 units. Find the value of a.

Solution:

Exercise 5.3

Question 1.
A, B and C are vertices of ∆ ABC. D, E and F are mid points of sides AB, BC and AC respectively. If the coordinates of A, D and F are (-3, 5), (5, 1) and (-5, -1) respectively. Find the coordinates of B, C and E.
Solution:

Question 2.
If A(10, 11) and B(2, 3) are the coordinates of end points of diameter of circle. Then find the centre of the circle.
Solution:

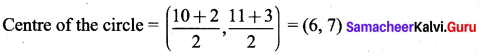
Question 3.
Find the coordinates of the point which divides the line segment joining the points (3, 1) and (5, 13) internally in the ratio 3 : 5.
Solution:

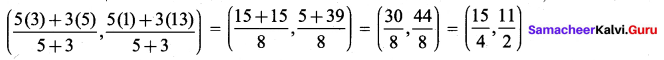
Exercise 5.4

Question 1.
Using section formula, show that the points A(7, -5), B(9, -3) and C(13, 1) are collinear.
Solution:

Question 2.
A car travels at an uniform speed. At 2pm it is at a distance of 5 km at 6 pm it is at a distance of 120 km. Using section formula, find at what distance it will reach 2 mid night.
Solution:

Question 3.
Find the coordinates of the point which divides the line segment joining the point A(3, 7) and B(-11, -2) in the ratio 5 : 1.
Solution:

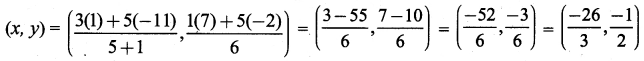
Exercise 5.5

Question 1.
Find the centroid of the triangle whose vertices are (2, -5), (5, 11) and (9, 9)
Solution:

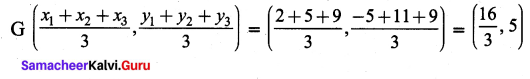
Question 2.
If the centroid of a triangle is at (10, -1) and two of its vertices are (3, 2) and (5, -11). Find the third vertex of the triangle.
Solution:

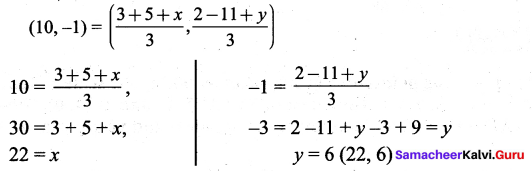
Exercise 5.6

Multiple Choice Questions :

Question 1.
The point (-2, 7) lies is the quadrant
(1) I
(2) II
(3) III
(4) IV
Hint:
(-, +) lies in II^nd quadrant
Solution:
(2) II

Question 2.
The point (x, 0) where x < 0 lies on
(1) OX
(2) OY
(3) OX’
(4) OY’
Hint:
(-, 0) lies on OX’
Solution:
(3) OX’

Question 3.
For a point A(a, b) lying in quadrant III.
(1) a > 0, b < 0
(2) a < 0, b < 0
(3) a > 0, b > 0
(4) a < 0, b > 0
Hint:
(-, -) lies in III^rd quadrant
Solution:
(2) a < 0, b < 0

Question 4.
The diagonal of a square formed by the points (1, 0) (0, 1) and (-1, 0) is
(1) 2
(2) 4
(3) \(\sqrt{2}\)
(4) 8
Hint:

Solution:
(1) 2

Question 5.
The triangle obtained by joining the points A(-5, 0) B(5, 0) and C(0, 6) is
(1) an isosceles triangle
(2) right triangle
(3) scalene triangle
(4) an equilateral triangle
Hint:
Triangles having two sides equal are called isosceles.
Solution:
(a) an isosceles triangle

Text Book Activities

Activity 1.
Plot the following points on a graph sheet by taking the scale as 1cm = 1 unit. Find how far the points are from each other? A (1, 0) and D (4, 0). Find AD and also DA. Is AD = DA? You plot another set of points and verify your result.

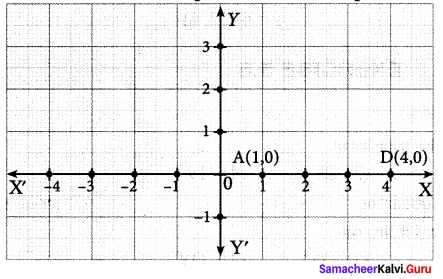
Solution:
AD = DA is correct.