You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.3
9th Maths Exercise 5.3 Question 1.
Find the mid-points of the line segment joining the points
(i) (-2, 3) and (-6, -5)
(ii) (8, -2) and (-8, 0)
(iii) (a, b) and (a + 2b, 2a – b)
(iv) \(\left(\frac{1}{2},-\frac{3}{7}\right)\) and \(\left(\frac{3}{2}, \frac{-11}{7}\right)\)
Solution:

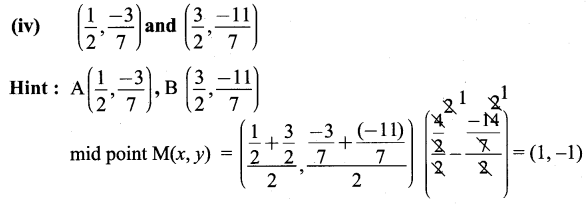
9th Maths Exercise 5.3 Solution Question 2.
The centre of a circle is (-4, 2). If one end of the diameter of the circle is (-3, 7) then find the other end.
Solution:
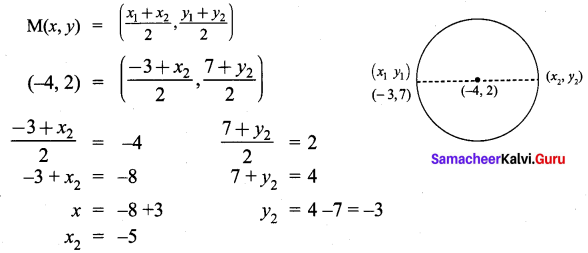
∴ The other end is (-5, -3)
9th Maths Exercise 5.3 Samacheer Kalvi Question 3.
If the mid-point (x, y) of the line joining (3, 4) and (p, 7) lies on 2x + 2y + 1 = 0, then
what will be the value of p?
Solution:
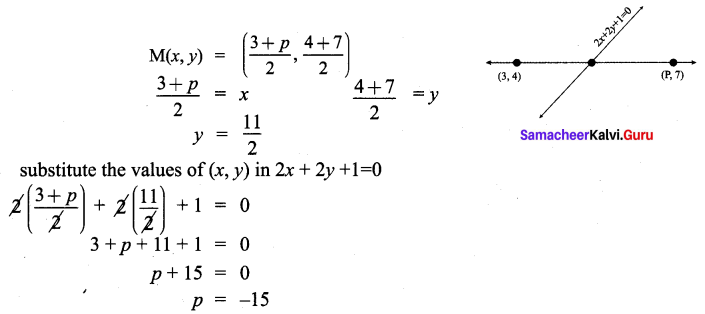
Class 9 Maths Exercise 5.3 Solution Question 4.
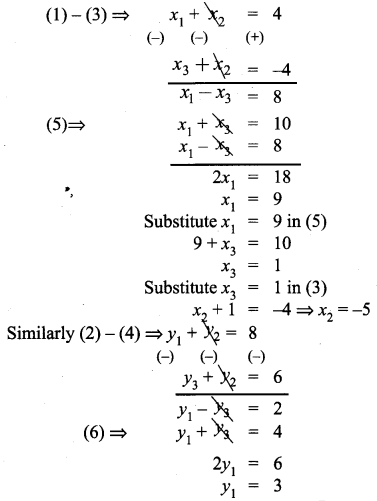
The midpoint of the sides of a triangle are (2, 4), (-2, 3) and (5, 2). Find the coordinates of the vertices of the triangle.
Solution:
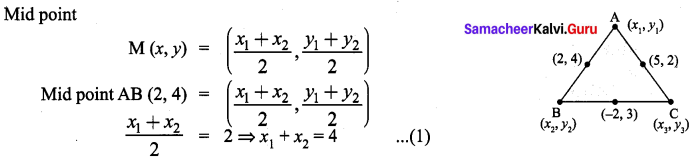

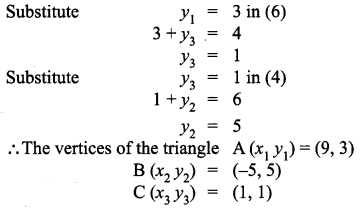
Class 9th Maths Chapter 5 Exercise 5.3 Question 5.
O(0, 0) is the centre of a circle whose one chord is AB, where the points A and B are (8, 6) and (10, 0) respectively. OD is the perpendicular from the centre to the chord AB. Find the coordinates of the mid-point of OD.
Solution:
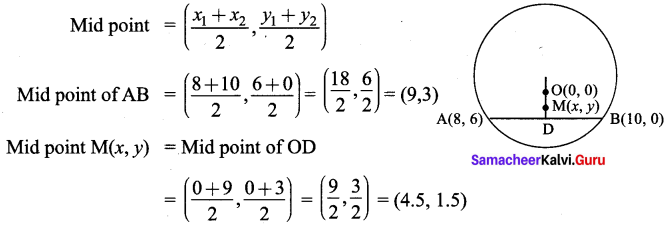
Exercise 5.3 Class 10 Samacheer Kalvi Question 6.
The points A (-5, 4), B (-1, -2) and C(5, 2) are the vertices of an isosceles right¬angled triangle where the right angle is at B. Find the coordinates of D so that ABCD is a square.
Solution:

Ex 5.3 Class 9 Maths Solutions Question 7.
The points A(-3, 6), B(0, 7) and C(1, 9) are the mid points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallelogram.
Solution:
In a parallelogram diagonals bisect each other and diagonals are not equal.



10th Maths Exercise 5.3 Samacheer Kalvi Question 8.
A (-3, 2), B (3, 2) and C(-3, -2)are the vertices of the right triangle, right angled at A. Show that the mid point of the hypotenuse is equidistant from the vertices.
Solution:

Hence proved