Students can Download Samacheer Kalvi 10th Maths Model Question Paper 3 English Medium Pdf, Samacheer Kalvi 10th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Model Question Paper 3 English Medium
Instructions
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III and IV are to be attempted separately.
- Question numbers 1 to 14 in Part I are Multiple Choice Quèstions of one-mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and.writing the option code and the corresponding answer.
- Question numbers 15 to 28 in Part II àre two-marks questions. These are to be answered in about one or two sentences.
- Question numbers 29 to 42 in Part III are five-marks questions. These are to be answered in about three to five short sentences.
- Question numbers 43 to 44 in Part IV are eight-marks questions. These are to be answered in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Max Marks: 100
PART – I
I. Choose the correct answer. Answer all the questions. [14 × 1 = 14]
Question 1.
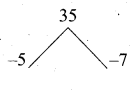
A = {a, b, p}, B = {2, 3}, C = {p, q, r, 5} then n[(A ∪ C) × B] is ……………. .
(1) 8
(2) 20
(3) 12
(4) 16
Answer:
(3) 12
![]()
Question 2.
If a, b, c are in G.P., then \(\frac{a-b}{b-c}\) is equal to ……………. .
(1) \(\frac{a}{b}\)
(2) \(\frac{b}{a}\)
(3) \(\frac{a}{c}\)
(4) \(\frac{c}{b}\)
Answer:
(1) \(\frac{a}{b}\)
Question 3.
If k + 2, 4k – 6, 3k – 2 are the 3 consecutive terms of an A.P, then the value of k is ……………. .
(1) 2
(2) 3
(3) 4
(4) 5
Answer:
(2) 3
Question 4.
If (x – 6) is the HCF of x2 – 2x – 24 and x2 – kx – 6 then the value of k is ……………. .
(1) 3
(2) 5
(3) 6
(4) 8
Answer:
(2) 5
Question 5.
If A is a 2 × 3 matrix and B is a 3 × 4 matrix, how many columns does AB have ……………. .
(1) 3
(2) 4
(3) 2
(4) 5
Answer:
(2) 4
Question 6.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. The length of the side AC is ……………. .
(1) 6 cm
(2) 4 cm
(3) 3 cm
(4) 8 cm
Answer:
(2) 4 cm
Question 7.
(2, 1) is the point of intersection of two lines.
(1) x – y – 3 = 0; 3x – y – 7 = 0
(2) x + y = 3; 3x + y = 7
(3) 3x + y = 3; x + y = 7
(4) x + 3y – 3 = 0; x – y – 1 = 0
Answer:
(2) x + y = 3; 3x + y = 7
Question 8.
If the ratio of the height of a tower and the length of its shadow is √3 : 1 , then the angle of elevation of the sun has measure ……………. .
(1) 45°
(2) 30°
(3) 90°
(4) 60°
Answer:
(4) 60°
Question 9.
A spherical ball of radius r1 units is melted to make 8 new identical balls each of radius r2 units. Then r1 : r2 is ……………. .
(1) 2:1
(2) 1:2
(3) 4:1
(4) 1:4
Answer:
(1) 2:1
![]()
Question 10.
The standard deviation of a data is 3. If each value is multiplied by 5 then the new variance is ……………. .
(1) 3
(2) 15
(3) 5
(4) 225
Answer:
(4) 225
Question 11.
A page is selected at random from a book. The probability that the digit at units place of the page number chosen is less than 7 is ……………. .
(1) \(\frac { 3 }{ 10 }\)
(2) \(\frac { 7 }{ 10 }\)
(3) \(\frac { 3 }{ 9 }\)
(4) \(\frac { 7 }{ 9 }\)
Answer:
(2) \(\frac { 7 }{ 10 }\)
Question 12.
The range of the relation R = {(x, x3)/x} is a prime number less than 13} is ……………. .
(1) {2,3,5,7,11}
(2) {4,9,25,49, 121}
(3) {8, 27,125, 343,1331}
(4) {1, 8, 27, 125, 343, 1331}
Answer:
(3) {8, 27,125, 343,1331}
Question 13.
If 1 + 2 + 3 + …. + n = k then 13 + 23 + 33 + ……… n3 is equal to ……………. .
(1) K2
(2) K3
(3) \(\frac{k(k+1)}{2}\)
(4) (k + 1)K3
Answer:
(1) K2
Question 14.
Two dice are thrown simultaneously. The probability of getting a doublet is ……………. .
(1) \(\frac { 1 }{ 36 }\)
(2) \(\frac { 1 }{ 3 }\)
(3) \(\frac { 1 }{ 6 }\)
(4) \(\frac { 2 }{ 3 }\)
Answer:
(3) \(\frac { 1 }{ 6 }\)
![]()
PART-II
II. Answer any ten questions. Question No. 28 is compulsory. [10 × 2 = 20]
Question 15.
ARelation R is given by the set {{x,y)/y = x + 3, x ∈ {0,1,2,3,4,5}}. Determine its domain and range.
Answer:
x = {0, 1, 2, 3, 4, 5} and y = x + 3
when x = 0 ⇒ y = 0 + 3 = 3
when x = 1 ⇒ y = 1 + 3 = 4 .
when x = 2 ⇒ y = 2 + 3 = 5
when x = 3 ⇒ y = 3 + 3 = 6
whenx = 4 ⇒ y = 4 + 3 = 7
when x = 5 ⇒ y = 5 + 3 = 8
R = {(0, 3) (1, 4) (2, 5) (3, 6) (4, 7) (5, 8)}
Domain = {0, 1, 2, 3, 4, 5}
Range = {3, 4, 5, 6, 7, 8}
Question 16.
Let f = {(-1,3), (0, -1), (2, – 9)} be a linear function from Z to Z. Find f(x).
Answer:
The linear equation is f(x) = ax + b
f(-1) = 3
a(-1) + b = 3
-a + b = 3 ….(1)
f(0) = -1
a(0) + b = -1
0 + b = -1
b = -1
Substitute the value of b = -1 in (1)
– a – 1 = 3
– a = 3 + 1 ⇒ – a = 4
a = -4
∴ The linear equation is -4(x) -1 = -4x – 1 (or) – (4x + 1)
Question 17.
Solve 8x = 1 (mod 11)
Answer:
8x ≡ 1 (mod 11) can be written as 8x – 1 = 11k, for some integer k.
x = \(\frac{11 k+1}{8}\)
When we put k = 5, 13, 21, 29,… . then 11 k + 1 is divisible by 8.
x = \(\frac{11 \times 5+1}{8}\) = 7
x = \(\frac{11 \times 13+1}{8}\) = 18
Therefore, the solutions are 7,18,29,40, …….
![]()
Question 18.
How many terms of the series 13 + 23 + 33 +……….. should be taken to get the sum 14400?
Answer:
13 + 23 + 33 +. . . + n3 = 14400
\(\left[\frac{n(n+1)}{2}\right]^{2}\) = 14400
\(\frac{n(n+1)}{2}\) = √14400
\(\frac{n(n+1)}{2}\) = 120 ⇒ n2 + n = 240
n2 + n – 240 =0
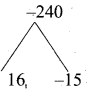
(n + 16) (n – 15) =0
(n + 16) = 0 or (n – 15) = 0
n = -16 or n = 15 (Negative will be omitted)
∴ The number of terms taken is 15
Question 19.
Given the L.C.M and G.C.D of the two polynomials are a3 – 10a2 + 11a + 70 and a – 7, the polynomial p(x) is a2 – 12a + 35 then find q(x).
Answer:
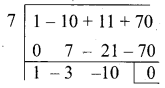
L.C.M. = a3 – 10a2 + 11a + 70
= (a – 7) (a2 – 3a – 10)
= (a – 7) (a – 5) (a + 2)
G.C.D. = (a – 7)
p(x) = a2 – 12a + 35
= (a – 5) (a – 7)
q(x) = \(\frac{\mathrm{LCM} \times \mathrm{GCD}}{p(x)}\)
= \(\frac{(a-7)(a-5)(a+2) \times(a-7)}{(a-5)(a-7)}\)
q(x) = (a + 2) (a – 7)
Question 20.
Find the square root of 9x2 – 24xy + 30xz – 40yz + 25z2 + 16y2
Answer:
\(\sqrt{9 x^{2}-24 x y+30 x z-40 y z+25 z^{2}+16 y^{2}}\)
= \(\sqrt{(3 x)^{2}+(4 y)^{2}+(5 z)^{2}-2(3 x)(4 y)-2(4 y)(5 z)+2(3 x)(5 z)}\)
= \(\sqrt{(3 x-4 y+5 z)^{2}}\) [using (a – b + c)2 = a2 + b2 + c2 – 2ab – 2bc + 2ca]
= |3x – 4y + 5z|
![]()
Question 21.
Construct a 3 × 3 matrix whose elements are aij = i2 j2
Answer:
The general 3 × 3 matrix is given by A = \(\left[ \begin{matrix} { a }_{ 11 } & { a }_{ 12 } & { a }_{ 13 } \\ { a }_{ 21 } & { a }_{ 22 } & { a }_{ 23 } \\ { a }_{ 31 } & { a }_{ 32 } & { a }_{ 33 } \end{matrix} \right]\) aij = i2 j2
a11 = 12 × 12 = 1 × 1 = 1;
a12 = 12 × 22 = 1 × 4 = 4;
a13 = 12 × 32 = 1 × 9 = 9;
a21 = 22 × 12 = 4 × 1 = 4;
a22 = 22 × 22 = 4 × 4 = 16;
a23 = 22 × 32 = 4 × 9 = 36;
a31 = 32 × 12 = 9 × 1 = 1;
a32 = 32 × 22 = 9 × 4 = 36;
a33 = 32 × 32 = 9 × 9 = 81;
Hence the required matrix is A = \(\left[ \begin{matrix} 1 & 4 & 9 \\ 4 & 16 & 36 \\ 9 & 36 & 81 \end{matrix} \right] \)
Question 22.
An artist has created a triangular stained glass window and has one strip of small length left before completing the window. She needs to figure out the length of left out portion based on the lengths of the other sides as shown in the figure.
Answer:
Given that AE = 3 cm, EC = 4 cm, CD = 10 cm, DB = 3 cm, AF = 5 cm.
Let FB be x
Using Ceva’s theorem we have
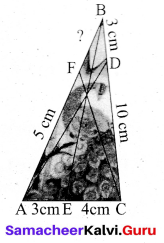
\(\frac{A E}{E C} \times \frac{C D}{D B} \times \frac{B F}{A F}=1\)
\(\frac{3}{4} \times \frac{10}{3} \times \frac{x}{5}=1\) \(\Rightarrow \frac{2 x}{4}=1\)
2x = 4 ⇒ x = \(\frac{4}{2}\) = 2
The value of BF = 2
Question 23.
Find the area of the triangle whose vertices are (-3, 5), (5, 6) and (5, -2)
Answer:
Plot the points in a rough diagram and take them in counter-clockwise order. Let the vertices be A(-3,5), B(5,-2), C(5,6)
The area of ∆ABC is
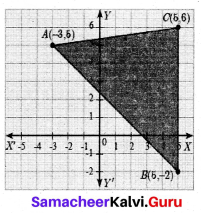
= \(\frac { 1 }{ 2 }\) {(x1y2 + x2y3 + x3y1) – (x2y1 + x3y2 + x1 y3)}
= \(\frac { 1 }{ 2 }\) {(6 + 30 + 25) – (25 – 10 – 18)}
= \(\frac { 1 }{ 2 }\) {(61 + 3)}
= \(\frac { 1 }{ 2 }\) (64) = 32 sq. units
![]()
Question 24.
From the top of a rock 50 √3 m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock.
Answer:
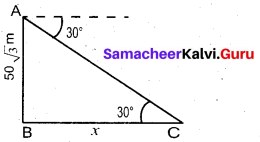
Let the distance of the car from the rock is “x” m
In the right ∆ ABC, tan 30° = \(\frac{A B}{B C}\)
\(\frac{1}{\sqrt{3}}=\frac{50 \sqrt{3}}{x}\)
X = 50 √3 × √3 = 50 × 3
= 150 m
∴ Distance of the car from the rock =150 m
Question 25.
If n = 5, x̄ = 6, Σx2 = 765, then calculate the coefficient of variation.
Answer:
Standard deviation (σ) = \(\sqrt{\frac{\Sigma x^{2}}{n}-\left(\frac{\Sigma x}{n}\right)^{2}}\)
\(=\sqrt{\frac{765}{5}-(6)^{2}}=\sqrt{153-36}=\sqrt{117}\)
σ = 10.816
Coefficient of variation = \(\frac{\sigma}{\bar{x}} \times 100 \%\)
= \(\frac{10.816}{6} \times 100 \%\) = 180.266%
Coefficient of variation = 180. 27%
Question 26.
The roots of the equation x2 + 6x – 4 = 0 are α, β. Find the quadratic equation whose roots are \(\frac{2}{\alpha}\) and \(\frac{2}{\beta}\).
Answer:
α and β are the roots of x2 + 6x – 4 = 0
α + β = -6 ; αβ = -4
Sum of the roots = \(\frac{2}{\alpha}+\frac{2}{\beta}\)
\(\frac{2 \beta+2 \alpha}{\alpha \beta}=\frac{2(\alpha+\beta)}{\alpha \beta}=\frac{2(-6)}{-4}\)
= 3
Product of the roots = \(\frac{2}{\alpha} \times \frac{2}{\beta}=\frac{4}{\alpha \beta}\)
= \(\frac{4}{-4}=-1\)
The quadratic equation is x2 – (sum of the roots) x + product of the roots = 0
∴ x2 – 3x – 1 = 0 .
Question 27.
If the points A(2, 5), B(4, 6) and C(8, a) are collinear, find the value of “a” using slope concept.
Answer:
Since the three points are collinear
Slope of line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = Slope of BC
\(\frac{6-5}{4-2}=\frac{a-6}{8-4}\)
\(\frac{1}{2}=\frac{a-6}{4}\)
2a – 12 = 4 ⇒ 2a = 16
a = \(\frac{16}{2}\) = 8
The value of a = 8
![]()
Question 28.
The king, Queen and Jack of clubs are removed from a deck of 52 playing cards and the remaining cards are shuffled. A card is drawn from the remaining cards, find the probability of getting (i) a card of clubs (ii) a queen of diamond
Answer:
Sample space (S) = (52 – 3) = 49
n (S) = 49
(i) Let A be the event of getting a card of clubs.
n(A) = (13 – 3) = 10
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{10}{49}\)
(ii) Let B be the event of getting a queen of diamond
n (B) = 1
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{1}{49}\)
PART-III
III. Answer any ten questions. Question No. 42 is compulsory. [10 × 5 = 50]
Question 29.
Find x if gff (x) = fgg (x), given f(x) = 3x + 1 and g(x) = x + 3.
Answer:
gff(x) = g [f {f{x)}} (This means “g of f of f of x”)
= g[f(3x + 1)] = g[3(3x + 1) + 1] = g(9x + 4)
g (9x + 4) = [ (9x + 4) + 3] = 9x + 7
fgg (x) = f[g{g (x)}] (This means “f of g of g of x”)
= f[g(x + 3)] = f[(x + 3) + 3] = f(x + 6)
f(x + 6) = [3(x + 6) + 1] = 3x + 19
These two quantities being equal, we get 9x + 7 = 3x + 19. Solving this equation we obtain x = 2.
Question 30.
Let A = {-l,l}and B = {0,2}. If the function f : A → B defined by f(x) = ax + b is an onto function? Find a and b.
Answer:
A = {-1, 1}; B = {0,2}
f(x) = ax + b
0 = -a + b
a – b = 0 …….. (1)
f(1) = a(1) + b
2 = a + b
a + b = 2 ………. (2)
Solving (1) and (2) we get
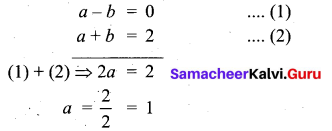
Substitute a = 1 in (1)
1 – b = 0 ⇒ -b = -1 ⇒ 6 = 1
The value of a = 1 and b = 1
![]()
Question 31.
Priya earned ₹15,000 in the first month. Thereafter her salary increases by ₹1500 per year. Her expenses are ₹13,000 during the first year and the expenses increases by ₹900 per year. How long will it take her to save ₹20,000 per month.
Answer:

Monthly savings form an A.P.
2000, 2600, 3200 ….
a = 2000 ; d = 2600 – 2000 = 600
Given tn = 20,000
tn = a + (n – 1) d
20000 = 2000 + (n – 1) 600
20000 = 2000 + 600n – 600
= 1400 + 600n
20000 – 1400 = 600n
1860o = 600n
n = \(\frac{18600}{600}\) = 31
He will take 31 years to save ₹20,000 per month
Question 32.
Find the sum to n terms of the series 0.4 + 0.44 + 0.444 + ……… to n terms
Answer:

Question 33.
Find the GCD of 6x3 – 30x2 + 60x – 48 and 3x3 – 12x2 + 21x – 18.
Answer:
Let, f(x) = 6x3 – 30x2 + 60x – 48 = 6(x3 – 5x2 + 10x – 8) and
g(x) = 3x3 – 12x2 + 21x – 18 = 3(x3 – 4x2 + 7x – 6)
Now, we shall find the GCD of x3 – 5x2 + 10x – 8 and x3 – 4x2 + 7x – 6

Here, we get zero as remainder.
GCD of leading coeffients 3 and 6 is 3
Thus GCD
[(6x3 – 30x2 + 60x – 48, 3x3 – 12x2 + 21x – 18)] = 3(x – 2)
![]()
Question 34.
If the roots of the equation (c2 – ab)x2 – 2(a2 – bc)x + b2 – ac = 0 are real and equal prove that either a = 0 (or) a3 + b3 + c3 = 3abc
Answer:
(c2 – ab)x2 – 2(a2 – bc)x + b2 – ac = 0
Here a = c2 – ab ; b = -2 (a2 – bc) ; c = b2 – ac
Since the roots are real and equal
Δ = b2 – 4ac
[-2 (a2 – bc)]2 – 4(c2 – ab) (b2 – ac) = 0
4(a2 – bc)2 – 4[c 2b2 – ac3 – ab3+ a2bc] = 0
Divided by 4 we get
(a2 – bc)2 [c2b2 – ac3 – ab2 + a2bc] = 0
a4 + b2c2 – 2a2bc – c2b2 + ac3 + ab3 – a2bc = 0
a4 + ab3 + ac3 – 3a2bc = 0
a(a3 +b3 + c3) = 3a2bc
a3 + b3 + c3 = \(\frac{3 a^{2} b c}{a}\)
a3 + b3 + c3 = 3abc
Hence it is proved
Question 35.
ABCD is a quadrilateral in which AB = AD, the bisector of ∠BAC and ∠CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.
Answer:
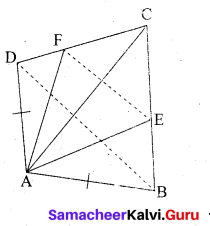
ABCD is a quadrilateral. AB = AD.
AE and AF are the internal bisector of ∠BAC and ∠DAC.
To prove: EF || BD.
Construction: Join EF and BD
Proof: In ∆ ABC, AE is the internal bisector of ∠BAC.
By Angle bisector theorem, we have,
∴ \(\frac{A B}{A C}=\frac{B E}{E C}\) …….. (1)
In ∆ ADC, AF is the internal bisector of ∠DAC
By Angle bisector theorem, we have,
\(\frac{A D}{A C}=\frac{D F}{F C}\)
∴ \(\frac{A B}{A C}=\frac{D F}{F C}\) (AB = AD given) …….. (2)
From (1) and (2), we get
\(\frac{B E}{E C}=\frac{D F}{F C}\)
Hence In ∆ BCD,
BD || EF (By converse of BPT)
![]()
Question 36.
Find the equation of a straight line passing through (1,-4) and has intercepts which are in the ratio 2:5
Answer:
Let the x-intercept be 2a and the y intercept 5a .
The equation of a line is \(\frac{x}{a}+\frac{y}{a}=1 \Rightarrow \frac{x}{2 a}+\frac{y}{5 a}=1\)
The line passes through the point (1, -A)
\(\frac{1}{2 a}+\frac{(-4)}{5 a}=1 \Rightarrow \frac{1}{2 a}-\frac{4}{5 a}=1\)
Multiply by 10a
(L.C.M of 2a and 5a is 10a)
5 – 8 = 10a ⇒ -3 = 10a .
a = \(\frac{-3}{10}\)
The equation of the line is \(\frac{x}{2(-3 / 10)}+\frac{y}{5(-3 / 10)}=1\)
\(\frac{x}{-3 / 5}+\frac{y}{-3 / 2}=1 \Rightarrow \frac{5 x}{-3}+\frac{2 y}{-3}=1\)
\(\frac{-5 x}{3}-\frac{2 y}{3}=1\)
Multiply by 3
-5x – 2y = 3 ⇒ -5x – 2y – 3 = 0
5x + 2y + 3 = 0
The equation of a line is 5x + 2y + 3 = 0
Question 37.
If \(\frac{\cos \theta}{1+\sin \theta}=\frac{1}{a}\), then prove that \(\frac{a^{2}-1}{a^{2}+1}\) = sin θ
Answer:
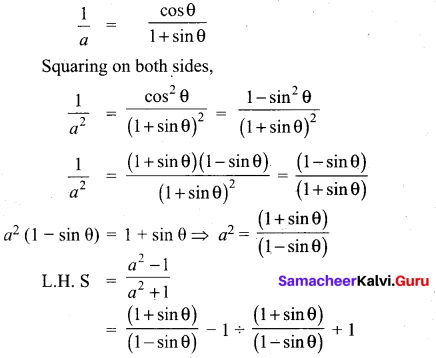
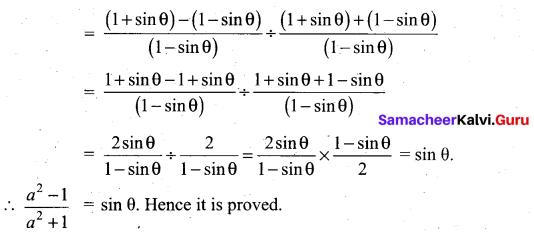
Question 38.
A toy is in the shape of a cylinder surmounted by a hemisphere. The height of the toy is 25 cm. Find the total surface area of the toy if its common diameter is 12 cm.
Answer:
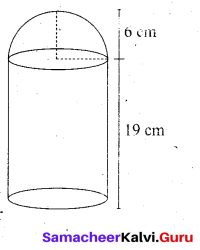
Let r and h be the radius and height of the cylinder respectively.
Given that, diameter d = 12 cm, radius r = 6 cm
Total height of the toy is 25 cm
Therefore, height of the cylindrical portion = 25 – 6 = 19 cm
T.S.A. of the toy = C.S.A. of the cylinder + C.S.A. of the hemisphere + Base Area of the cylinder
= 2πrh + 2πr2 + πr2
= πr(2h + 3r) sq.unis
= \(\frac { 22 }{ 7 }\) × 6(38 + 18)
= \(\frac { 22 }{ 7 }\) × 6 × 56 = 1056
Therefore, T.S.A. of the toy is 1056 cm2
![]()
Question 39.
A coin is tossed thrice. Find the probability of getting exactly two heads or atleast one tail or two consecutive heads.
Answer:
Sample space = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n (S) = 8
Let A be the event of getting exactly two heads.
A = {HHT, HTH, THH}
n(A) = 3
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{3}{8}\)
Let B be the event of getting atleast one tail
B = {HHT, HTH, HTT, THH, THT, TTH, TTT}
n(B) = 7
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{7}{8}\)
Let C be the event of getting consecutively
C = {HHH, HHT, THH}
n(C) = 3
P(C) = \(\frac{n(\mathrm{C})}{n(\mathrm{S})}=\frac{3}{8}\)
A ∩ B = { HHT, HTH, THH}
n(A ∩ B) = 3
p(A ∩ B) = \(\frac{n(\mathrm{A} \cap \mathrm{B})}{n(\mathrm{S})}=\frac{3}{8}\)
B ∩ C = {HHT, THH}
n(B ∩ C) = 2
p(B ∩ C) = \(\frac{n(\mathrm{B} \cap \mathrm{C})}{n(\mathrm{S})}=\frac{2}{8}\)
A ∩ C = {HHT, THH}
n(A ∩ C) = 2
P(A ∩ C) = \(\frac{n(\mathrm{A} \cap \mathrm{C})}{n(\mathrm{S})}=\frac{2}{8}\)
(A ∩ B ∩ C) = 2
P(A ∩ B ∩ C) = \(\frac{n(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})}{n(\mathrm{S})}=\frac{2}{8}\)
P(A∪B∪C) = P(A) + P(B) + P(C) -P(A ∩ B) – p(B ∩ C) – P(A ∩ C) + P(A∩B∩C)
\(=\frac{3}{8}+\frac{7}{8}+\frac{3}{8}-\frac{3}{8}-\frac{2}{8}-\frac{2}{8}+\frac{2}{8}\)
\(=\frac{3}{8}+\frac{7}{8}-\frac{2}{8}\)
\(=\frac{10-2}{8}=\frac{8}{8}\) = 1
The probability is 1
Question 40.
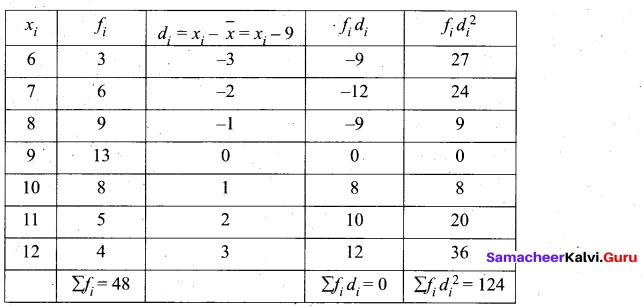
The following table show the marks obtained by 48 students in a quiz competition in mathematics calculate the standard deviation.
Answer:

Ans.
Let us form the following table using given data

![]()
Question 41.
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4m, and slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also find the cost of canvas of the tent at the rate of ₹500 per m2.
Answer:
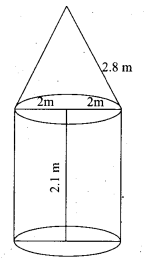
For conical portion
Radius (r) = 2m
Slant height (l) = 2.8 m
For cylindrical portion
Radius (R) = 2m
Height (H) = 2.1 m
Area of canvas used for the tent = Curved surface area of a cone + curved area of the cylinder
= πrl + 2πRH
= π(2 × 2.8 + 2 × 2 × 2.1)
= \(\frac { 22 }{ 7 }\) (5.6+ 8.4)
= \(\frac { 22 }{ 7 }\) × 14 sq.m
= 44 sq. m
Cost of the canvas at the rate of ₹500 per m2 = ₹ 500 × 44
= ₹ 22000
Question 42.
Seven years ago Ramkumar’s age was five time the square of Daniel’s age. Three years hence Daniel age will be two fifth of Ramkumar’s age. Find their present ages.
Answer:
Seven years ago, let Daniel’s age be x years
Seven years ago, Ramkumar age was 5x2 years
Daniel’s present age = (x + 7) year
Ramkumar’s present age = 5x2 + 7 years
Three years hence
Daniel’s age = (x + 7 + 3) year = (x + 10) years
Ramkumar’s age = (5x2 + 7 + 3) year = (5x2 + 10) years
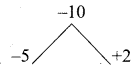
By the given condition
x + 10 = \(\frac { 2 }{ 5 }\) (5x2 +10)
5x + 50 = 10x2 + 20
10x2 – 5x – 30 = 0
2x2 – x – 6 = 0
2x2 – 4x + 3x – 6 = 0
2x (x – 2) + 3(x – 2) = 0
(x – 2) (2x + 3) = 0
x – 2 = 0 or 2x + 3 = 0
x = 2 or x = \(\frac { -3 }{ 2 }\)
∴ x = 2 (age will not be negative)
Hence Daniel age = 9 years (2 + 7)
Ramkumar’s age = 27 years [5(2)2 + 7]
![]()
PART – IV
IV. Answer all the questions. [2 × 8 = 16]
Question 43.
(a) Construct a ∆PQR in which PQ = 8 cm, ∠R = 60° and the median RG from R to PQ is 5.8 cm. Find the length of the altitude from R to PQ.
Answer:
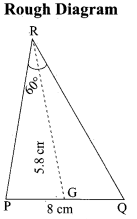
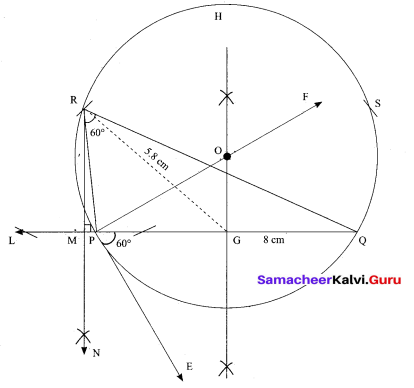
Step 1 : Draw a line segment PQ = 8 cm.
Step 2 : At P, draw PE such that ∠QPE = 60°.
Step 3 : At P, draw PF such that ∠EPF = 90°.
Step 4 : Draw the perpendicular bisector to PQ, which intersects PF at O and PQ at G.
Step 5 : With O as centre and OP as radius draw a circle.
Step 6 : From G mark arcs of radius 5.8 cm on the circle. Mark them as R and S.
Step 7 : Join PR and RQ. Then ∆PQR is the required triangle.
Step 8 : From R draw a line RN perpendicular to LQ.
LQ meets RN at M
Step 9: The length of the altitude is RM = 3.5 cm.
![]()
[OR]
(b) Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure the lengths of the tangents.
Answer:
Radius = 3cm, Distance = 5 cm.
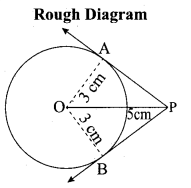
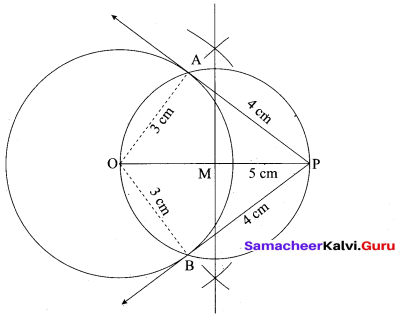
Steps of construction:
- With O as centre, draw a circle of radius 3 cm.
- Draw a line OP = 5 cm.
- Draw a perpendicular bisector of OP, which cuts OP at M.
- With M as centre and MO as radius draw a circle which cuts previous circles at A and B.
- Join AP and BP, AP and BP are the required tangents.
The length of the tangent PA = PB = 4 cm
Verification: In the right angle triangle OAP
PA2 = OP2 – OA2
= 52 – 32 .
= 25 – 9 = 16
PA = √l6 = 4 cm
Length of the tangent = 4 cm
![]()
Question 44.
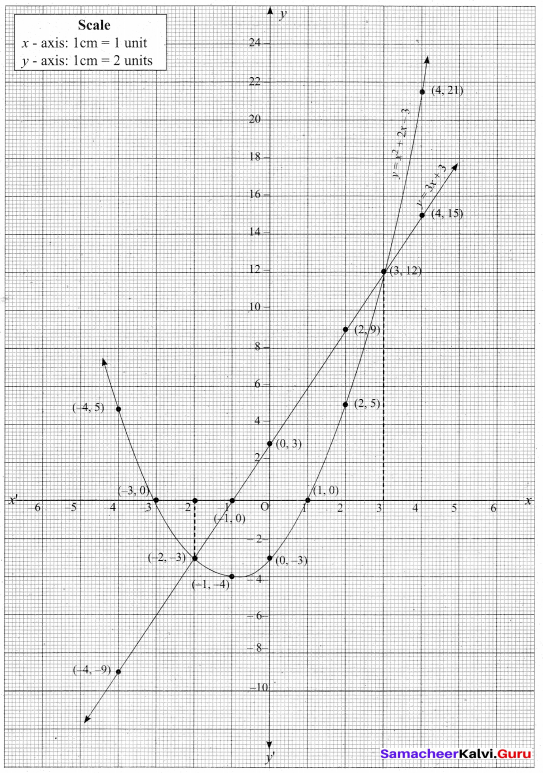
(a) Draw the graph of y = (x – 1) (x + 3) and hence solve x2 – x – 6 = 0
Answer:
y = (x – 1) (x + 3)
y = x2 + 2x – 3
(i) Draw the graph of y = x2 + 2x – 3 by preparing the table of values given below.
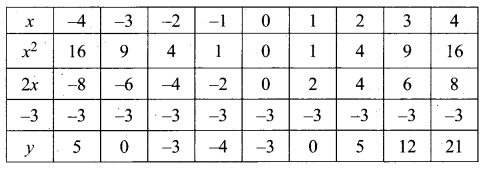
(ii) Plot the points (-4, 5), (-3, 0), (-2, -3), (-1, -4), (0, -3), (1, 0), (2, 5), (3, 12) and (4, 21) on the graph sheet using suitable scale.
(iii) To solve x2 – x – 6 = 0 subtract x2 – x – 6 = 0 from y = x2 + 2x – 3
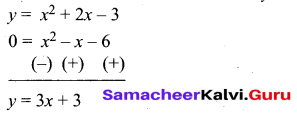
(iv) Draw the graph of y = 3x + 3 by preparing the table.

(v) The straight line cuts the curve at (-2, -3) and (3, 12). Draw perpendicular lines from the point to X – axis.
The line cut the X – axis at -2 and 3.
The solution set is (-2, 3)
![]()
[OR]
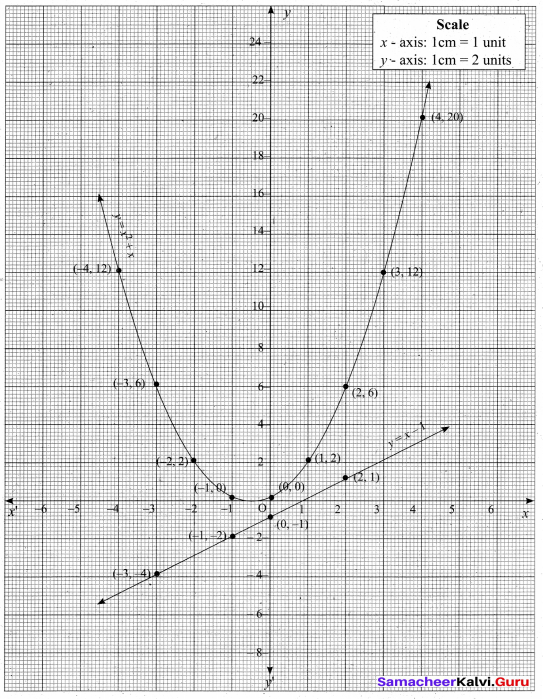
(b) Draw the graph of y = x2 +x and hence solve x2 + 1=0
Answer:
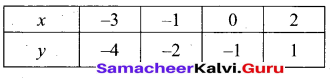
Let y = x2 + x
(i) Draw the graph of y = x2 + x by preparing the table.

(ii) Plot the points (-4, 12), (-3, 6), (-2, 2), (-1, 0), (0, 0), (1, 2), (2, 6), (3, 12) and (4, 20).
(iii) Join the points by a free hand to get smooth curve.
(iv) To solve x2 + 1 = 0, subtract x2 + 1 = 0 from x2 + x we get.
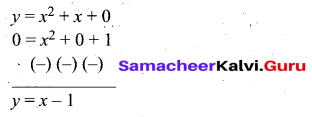
The equation represent a straight line. Draw a line y = x – 1
Observe the graph of y = x2 + 1 does not interset the parabola y = x2 + x This x2 + 1 has no real roots.