Tamil Nadu 11th Physics Model Question Paper 1 English Medium

Students can Download Tamil Nadu 11th Physics Model Question Paper 1 English Medium Pdf, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Physics Model Question Paper 1 English Medium

Instructions:

1. The question paper comprises of four parts
2. You are to attempt all the parts. An internal choice of questions is provided wherever: applicable
3. All questions of Part I, II, III, and IV are to be attempted separately
4. Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
6. Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
7. Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.

Time: 3 Hours
Max Marks: 70

Part-I

Answer all the questions. [15 x 1 = 15]

Question 1.
A dimensionless quantity
(a) never has a unit
(b) always has a unit
(c) may have or have not a unit
(d) none of the above
Answer:
(c) may have or have not a unit

Question 2.
The magnitude of average velocity is equal to average speed when the particle moving with
(a) variable speed
(b) constant velocity
(c) variable velocity
(d) constant acceleration
Answer:
(b) constant velocity

Question 3.
Two blocks of masses m and 2 m are placed on a smooth horizontal surface as shown. In the first case only a force F₁ is applied from the left. Later only a force F₂ is applied from the-right. If the force acting at the interface of the two blocks in the two cases is same, then

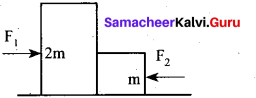
F₁ : F₂ is ……………. .
(a) 1 : 1
(b) 1 : 2
(c) 2 : 1
(d) 1 : 3
Answer:
(c) 2 : 1

Question 4.
The instantaneous angular position of a point on a rotating wheel is given by the equation θ(t) = 2t³ – 6t². The torque on the wheel becomes zero at …………… .
(a) t = 1s
(b) t = 0.5s
(c) t = 0.25 s
(d) t = 2s
Answer:
(a) t = 1s

Hint: According to question, torque τ = 0 it means that \(\propto=\frac{d^{2} \theta}{d t^{2}}\)

Question 5.
The workdone by the conservative force for a closed path is
(a) always negative
(b) zero
(c) always positive
(d) not defined
Answer:
(b) zero

Question 6.
The rain drops are spherical in shape due to
(a) gravity
(b) due to contraction
(c) surface tension
(d) viscosity
Answer:
(c) surface tension

Question 7.
Which of the following diagrams does not represent a streamline flow?

Answer:

Question 8.
When a spiral spring is stretched by a force, the resultant strain is
(a) volume
(b) shear
(c) tensile
(d) all these
Answer:
(b) shear

Question 9.
In a simple harmonic oscillation, the acceleration against displacement for one complete oscillation will be
(a) an ellipse
(b) a circle
(c) a parabola
(d) a straight line
Answer:
(d) a straight line

Question 10.
Beats are produced by two progressive waves. Maximum loudness at the waxing is x times the loudness of each wave. The value of x is
(a) 1
(b) \(\sqrt{2}\)
(c) 2
(d) 4
Answer:
(d) 4

Hint: The maximum amplitude is the sum of two amplitude, i.e. a + a = 2a Hence, maximum intensity is proportional to 4a² Loudness of one wave is given by \(x=\frac{4 a^{2}}{a^{2}}=4\)

Question 11.
Water does not freeze at the bottom of the lakes in winter because ………… .
(a) ice is a good conductor of heat
(b) ice reflects heat and light
(c) of anomalous expansion of water between 4°C to 0°C
(d) nothing can be said ‘
Answer:
(c) of anomalous expansion of water between 4°C to 0°C

Question 12.
According to Stefan Boltzmann law, the heat radiated by a black body is directly proportional to
(a) T²
(b) T³
(c) T⁴
(d) T⁸
Answer:
(c) T⁴

Question 13.
Two springs of spring constant 1500 Nm^-1 and 300 Nm^-1 respectively are stretched with the same force. They will have potential energy in the ratio
(a) 1 : 2
(b) 2 : 1
(c) 1 : 4
(d) 4 : 1
Answer:
(b) 2 : 1

Hint:

Question 14.
When the axis of rotation passes through its centre of gravity, then the moment of inertia of a rigid body is ………………. .
(a) reduced to its minimum value
(b) zero
(c) increased to its maximum value
(d) infinity
Answer:
(a) reduced to its minimum value

Question 15.
Power is given by
\((a) \mathrm{P}=\frac{\overrightarrow{\mathrm{F}}}{\overline{\mathrm{V}}}
(b) \frac{\vec{F}^{2}}{\vec{V}}
(c) \frac{\overrightarrow{\mathrm{F}}}{\overrightarrow{\mathrm{V}}^{2}}
(d) \overrightarrow{\mathbf{F}} \cdot \overrightarrow{\mathbf{V}}\)
Answer:
\((d)\overrightarrow{\mathbf{F}} \cdot \overrightarrow{\mathbf{V}}\)

Part-II

Answer any six questions in which Q. No 23 is compulsory. [6 x 2 = 12]

Question 16.
In solids both longitudinal and transverse waves are possible, but transverse waves are not produced in gases. Why?
Answer:
It is because transverse waves travel in the form of crests and troughs which involves the change in shape. For the propagation of transverse waves, medium should posses elasticity of shape. Therefore transverse waves are not produced in gases.

Question 17.
It is possible that the brakes of a bus are so perfect that the bus stops instantaneously? If not, why?
Answer:
No. If the car stops instantaneously, this means that the velocity is reduced to zero is an infinitesimally small interval of time. This would further mean that the car has infinite deceleration. This is not possible. Thus, we cannot have a car which can stop instantaneously.

Question 18.
Why does a rubber ball bounce higher on hills than in plains?
Answer:
The maximum height attained by the projectile is inversely proportional to acceleration due to gravity. At greater height, acceleration due to gravity will be lesser than plains. So ball can bounce higher in hills than in plains.

Question 19.
State conservation of angular momentum.
Answer:
The law of conservation of angular momentum states that when no external torque acts on the body the net angular momentum of a rotating rigid body remains constant.

Question 20.
Mountain roads rarely go straight up but wind up gradually. Why?
Answer:
Frictional force f is given by f = μ mg cos θ. If the roads go straight up the angle of slope θ would be large and frictional force will be less and vehicles may slip.

Question 21.
State Newton’s second law.
Answer:
The force acting on an object is equal to the rate of change of its momentum
\(\overrightarrow{\mathrm{F}}=\frac{d \vec{p}}{d t}\)

Question 22.
Why the specific heat capacity of constant pressure is greater than the specific heat capacity at constant volume?
Answer:
It implies that to increase the temperature of the gas at constant volume requires less heat than increasing the temperature of the gas at constant pressure. In other words s_p is always greater than s_v.

Question 23.
Define angle of contact.
Answer:
The angle between tangents drawn at the point of contact to the liquid surface and solid surface inside the liquid is called the angle of contact for a pair of solid and liquid.

Question 24.
Define forced oscillation. Give an example.
Answer:
The body executing vibration initially vibrates with its natural frequency and due to the presence of external periodic force, the body later vibrates with the frequency of the applied periodic force. Such vibrations are known as forced vibrations.
Example: Sound boards of stringed instruments.

Part – III

Answer any six questions in which Q.No. 29 is compulsory. [6 x 3 = 18]

Question 25.
Convert G = 6.67 x 10^-11 Nm² kg^-2 to cm³ g^-1 s^-2
Answer:
G = 6.67 x 10^-11 N m² kg^-2
= 6.67 x 10^-11 (kg m s^-2) (m² kg^-2)
= 6.67 x 10^-11 kg^-1 m³ s^-2
= 6.67 x 10^-11 (1000 g)^-1 (100 cm)³ (s^-2) .
= 6.67 x 10^-11 x \(\frac{1}{1000}\) x 100 x 100 x 100 g^-1 cm³ s^-2
= 6.67 x 10^-8 g^-1 cm³ s^-2

Question 26.
A object is thrown with initial speed 5 ms^-1 with an angle of projection 30°. What is the height and range reached by the particle?
Answer:
Data: Initial speed = 5 ms^-1.
Angle of projection = 30°

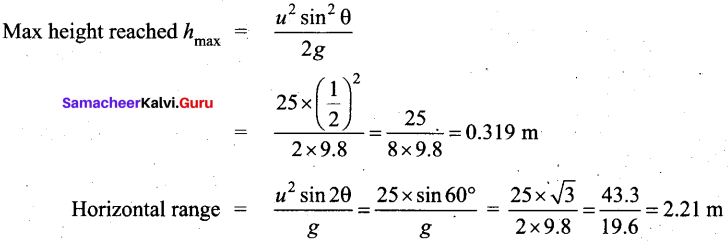
Question 27.
Three point masses m₁, m₂, m₃ are located at the vertices of equilateral triangle of side “a”. What is the moment of inertia of system about an axis along the altitude of triangle passing through m₁.
Answer:

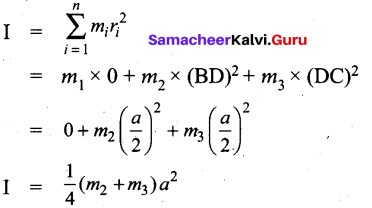
Question 28.
A box is pulled with a force of 25 N to produce a displacement of 15 m. If the angle between the force and displacement is 30°, find the work done by the force?
Answer:

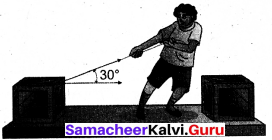
Force, F = 25 N
Displacement, dr = 15 m
Angle between F and dr, θ = 30°
Work done, W = F dr cos θ
W = 25 x 15 x cos 30 = 25 x 15 x \(\frac{\sqrt{3}}{2}\)
W = 324.76 J

Question 29.
The time period of a mass suspended by a spring (force constant K) is T. If the spring is cut into three equal pieces, what will be the force constant of each part? If the same mass be suspended from one piece what will be the periodic time?
Answer:
Consider the spring be made of a combination of three springs in series each of spring constant k. The effective spring constant K is given by
\(\frac{1}{K}=\frac{1}{k}+\frac{1}{k}+\frac{1}{k}=\frac{3}{k}\)
or K = \(\frac{k}{3}\) or k = 3K

∴ Time period of vibration of a body attached to the end of this spring,

When the spring is cut into three pieces, the spring constant k, time period of vibration of a body attached to the end of this spring,

T₁ = 2π\(\sqrt{\frac{m}{k}}\) ………………………………. (2)

From eqns. (1) and (2)
\(\frac{T_{1}}{T}=\frac{1}{\sqrt{3}} \text { or } T_{1}=\frac{T}{\sqrt{3}}\)

Question 30.
Give various applications of viscosity.
Answer:

1. The oil used as a lubricant for heavy machinery parts should have a high viscous coefficient. To select a suitable lubricant, we should know its viscosity and how it varies with temperature. [Note: As temperature increases, the viscosity of the liquid decreases].
2. Also, it helps to choose oils with low viscosity used in car engines (light machinery).
3. The highly viscous liquid is used to damp the motion of some instruments and is used as brake oil in hydraulic brakes.
4. Blood circulation through arteries and veins depends upon the viscosity of fluids.
5. Millikan conducted the oil drop experiment to determine the charge of an electron. He used the knowledge of viscosity to determine the charge.

Question 31.
Write a note on quasi-static process.
Answer:
A quasi-static process is an infinitely slow process in which the system changes its variables (P,V,T) so slowly such that it remains in thermal, mechanical and chemical equilibrium with its surroundings throughout.

Question 32.
A body cools from 60°C to 50°C in 10 min of room after 10 more minute.
Answer:
According to Newton’s law of cooling

Question 33.
Consider two springs with force constants 1 Nm^-1 and 2 Nm^-1 connected in parallel. Calculate the effective spring constant (k_p) and comment on k_p.
Answer:
k₁ = 1 Nm^-1, k₂ = 2 Nm^-1
k_p = k₁ + k₂ Nm^-1
k_p = 1 + 2 = 3 Nm^-1
k_p > k₁ and k_p > k₂

Therefore, the effective spring constant is greater than both k₁ and k₂.

Part-IV

Answer all the questions. [5 x 5 = 25]

Question 34.
(a) Describe the construction and working of venturimeter and obtain an equation for the volume of liquid flowing per second through a wider entry of the tube.
Answer:

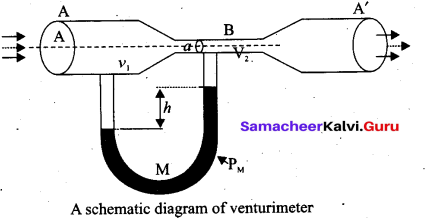
Venturimeter: This device is used to measure the rate of flow (or say flow speed) of the incompressible fluid flowing through a pipe. It works on the principle of Bernoulli’s theorem. It consists of two wider tubes A and A’ (with cross sectional area A) connected by a narrow tube B (with cross sectional area a). A manometer in the form of U-tube is also attached between the wide and narrow tubes. The manometer contains a liquid of density ‘p_m’.

Let P₁ be the pressure of the fluid at the wider region of the tube A. Let us assume that the fluid of density ‘p’ flows from the pipe with speed ‘v₁’ and into the narrow region, its speed increases to ‘v₂‘ According to the Bernoulli’s equation, this increase in speed is accompanied by a decrease in the fluid pressure P₂ at the narrow region of the tube B. Therefore, the pressure difference between the tubes A and B is noted by measuring the height difference (ΔP = P₁ – P₂) between the surfaces of the manometer liquid.

From the equation of continuity, we can say that Av₁ = av₂ which means that
\(v_{2}=\frac{\mathbf{A}}{a} v_{1}\)

Using Bernoulli’s equation,

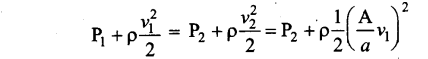
From the above equation, the pressure difference

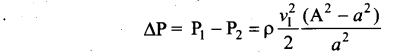
Thus, the speed of flow of fluid at the wide end of the tube

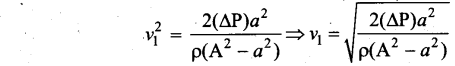
The volume of the liquid flowing out per second is

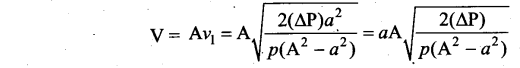
[OR]

(b) Derive the time period of satellite orbiting the Earth.
Answer:
Time period of the satellite: The distance covered by the satellite during one rotation in its orbit is equal to 2π(R_E + h) and time taken for it is the time period T. Then,

Squaring both sides of the equation (2) we get,

Equation (3) implies that a satellite orbiting the Earth has the same relation between time and distance as that of Kepler’s law of planetary motion. For a satellite orbiting near the surface of the Earth, h is negligible compared to the radius of the Earth R_E. Then,

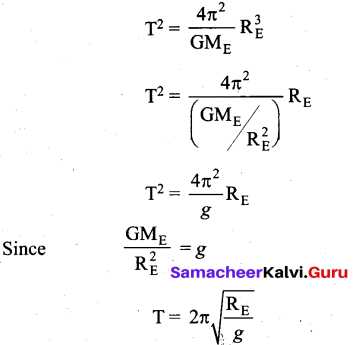
By substituting the values of R_E = 6.4 x 10⁶ m and g = 9.8 ms^-2, the orbital time period is obtained as T = 85 minutes.

Question 35.
(a) State and explain work energy principle.
(b) Mention any three examples for it.
Answer:
(a) Work and energy are equivalents. This is true in the case of kinetic energy also. To prove this, let us consider a body of mass m at rest on a ffictionless horizontal surface. The work (W) done by the constant force (F) for a displacement (s) in the same direction is,
W = Fs ………………………….. (1)

The constant force is given by the equation,
F = ma ………………………….. (2)

The third equation of motion can be written as,
v² = u² + 2as
\(a=\frac{v^{2}-u^{2}}{2 s}\)

Substituting for a in equation (2),

Substituting equation (3) in (1),

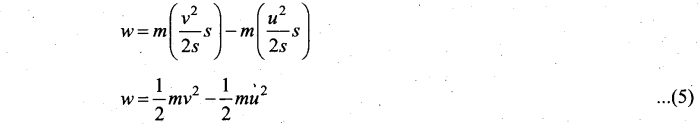
(b) (i) If the work done by the force on the body is positive then its kinetic energy increases.
(ii) If the work done by the force on the body is negative then its kinetic energy decreases.
(iii) If there is no work done by the force on the body then there is no change in its kinetic energy, which means that the body has moved at constant speed provided its mass remains constant.
(iv) When a particle moves with constant speed in a circle, there is no change in the kinetic energy of the particle. So according to work energy principle, the work done by centripetal force is zero.

[OR]

(b) Derive an expression for time taken by the round object to reach the ground on inclined plane.
Answer:
Let us assume a round object of mass m and radius R is rolling down an inclined plane without slipping as shown in figure. There are two forces acting on the object along the inclined plane. One is the component of gravitational force (mg sin θ) and the other is the static frictional force (f). The other component of gravitation force (mg cos θ) is cancelled by the normal force (N) exerted by the plane. As the motion is happening along the incline, we shall write the equation for motion from the free body diagram (FBP) of the object.

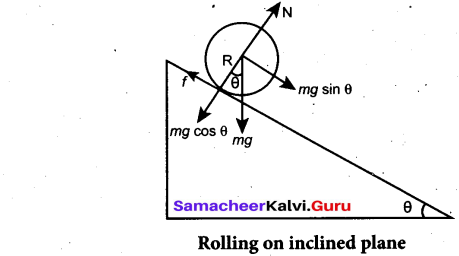
For translational motion, mg sin0 is the supporting force and f is the opposing force,
mg sinθ f = ma

For rotational motion, let us take the torque with respect to the center of the object. Then mg sin θ cannot cause torque as it passes through it but the frictional force/can set torque of Rf.
Rf = Iα
By using the relation, a = rα, and moment of inertia I = mK², we get,

We can also find the expression for final velocity of the rolling object by using third equation of motion for the inclined plane.

v² = u² + las. If the body starts rolling from rest, u = 0. When h is the vertical height of the incline, the length of the incline s is, s = \(\frac{h}{\sin \theta}\)

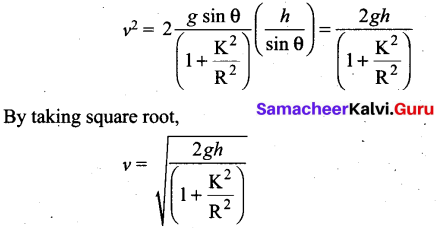
The time taken for rolling down the incline could also be written from first equation of motion as, v = u + at. For the object which starts rolling from rest, u = 0. Then,

The equation suggests that for a given incline, the object with the least value of radius of’ gyration K will reach the bottom of the incline first.

Question 36.
(a) Define heat engine. Derive the expression for carnot engine efficiency.
Answer:
Head engine: Heat engine is a device which takes heat as input and converts this heat in to work by undergoing a cyclic process.

Efficiency of a Carnot engine: Efficiency is defined as the ratio of work done by the working substance in one cycle to the amount of heat extracted from the source.

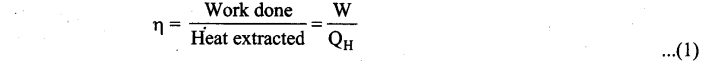
From the first law of thermodynamics, W = Q_H – Q_L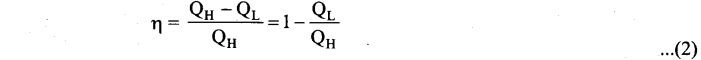
Applying isothermal conditions, we get,

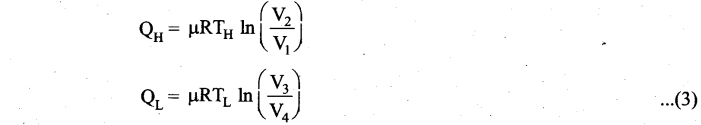
Here we omit the negative sign. Since we are interested in only the amount of heat (QL) ejected into the sink, we have

By applying adiabatic conditions, we get,

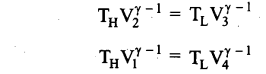
By dividing the above two equations, we get

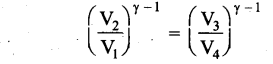
Which implies that \(\frac{V_{2}}{V_{1}}=\frac{V_{3}}{V_{4}}\) ………………………… (5)
Substituting equation (5) in (4), we get

Note: T_L and T_H should be expressed in Kelvin scale.

Important results:

1. η is always less than 1 because T_L is less than T_H. This implies the efficiency cannot be 100%.
2. The efficiency of the Carnot’s engine is independent of the working substance. It depends only on the temperatures of the source and the sink. The greater the difference between the two temperatures, higher the efficiency.
3. When T_H = T_L the efficiency η = 0. No engine can work having source and sink at the same temperature.

[OR]

(b) Derive the expression for moment of inertia of a rod about its center and perpendicular to the rod.
Answer:
Let us consider a uniform rod of mass (M) and length (1) as shown in figure. Let us find an expression for moment of inertia of this rod about an axis that passes through the center of mass and perpendicular to the rod. First an origin is to be fixed for the coordinate system so that it coincides with the center of mass; which is also the geometric center of the rod. The rod is now along the x axis. We take an infinitesimally small mass (dm) at a distance (x) from the origin. The moment of inertia (dI) of this mass (dm) about the axis is,

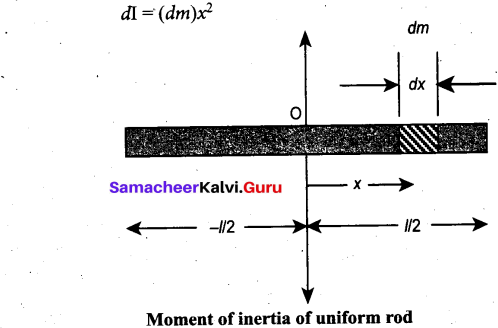
As the mass is uniformly distributed, the mass per unit length (λ) of the rod is, λ = \(\frac{M}{l}\)

The (dm) mass of the infinitesimally small length as, dm = λdx = \(\frac{M}{l}\) dx
The moment of inertia (I) of the entire rod can be found by integrating dl,

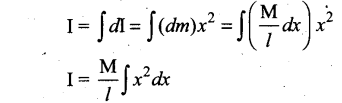
As the mass is distributed on either side of the origin, the limits for integration are taken from to – l/2 to l/2.

Question 37.
(a) Show that the resultant intensity at any point depends on the phase difference at that point in interference of waves.
Answer:
Consider two harmonic waves having identical frequencies, constant phase difference φ and same wave form (can be treated as coherent source), but having amplitudes A₁ and A₂, then
y₁ = A₁ sin (kx – ωt) …………………………. (1)
y₂ = A₂ sin (kx – ωt + φ) ……………………. (2)

Suppose they move simultaneously in a particular direction, then interference occurs (i.e., overlap of these two waves). Mathematically
y = y₁ + y₂ ………………………………. (3)

Therefore, substituting equation (1) and equation (3) in equation (3), we get
y = A₁ sin (kx – ωt) + A₂ sin (kx – ωt + φ)

Using trigonometric identity sin (α + β) = (sin α cos β + cos α sin β), we get
y = A₁ sin (kx – ωt) +A₂ [sin (kx – ωt) cos φ + cos (kx – ωt) sin φ]
y = sin (kx – ωt) (A₁ + A₂ cos φ) + A₂ sin φ cos (kx – ωt) …………………………. (4)

Let us re-define A cos θ = (A₁ + A₂ cos φ) ……………………………….. (5)
and A sin θ = A₂ sin φ …………………………………. (6)

then equation (4) can be rewritten as y = A sin (kx – ωt) cos θ + A cos (kx – ωt) sin θ
y = A (sin (kx – ωt) cos θ + sin θ cos (kx – ωt))
y = A sin (kx – ωt + 9) …………………………….. (7)

By squaring and adding equation (5) and equation (6), we get
A₂ = A₁2 + A₂2 + 2A₁ A₂ cos φ …………………………… (8)

Since, intensity is square of the amplitude (I = A₂), we have
I = I₁ + I₂ + 2\(2 \sqrt{\mathrm{I}_{1} \mathrm{I}_{2}}\) cos φ …………………………….. (9)

This means the resultant intensity at any point depends on the phase difference at that point.

(i) For constructive interference: When crests of one wave overlap with crests of another wave, their amplitudes will add up and we get constructive interference. The resultant wave has a larger amplitude than the individual waves as shown in figure (a).

The constructive interference at a point occurs if there is maximum intensity at that point, which means that
cos φ = + 1 ⇒ φ = 0, 2π, 4π,… = 2nπ,
where n = 0, 1, 2,…

This is the phase difference in which two waves overlap to give constructive interference. Therefore, for this resultant wave,
\(I_{\text {maximum }}=(\sqrt{I_{1}}+\sqrt{I_{2}})^{2}=\left(A_{1}+A_{2}\right)^{2}\)

Hence, the resultant amplitude A = A₁ + A₂

(ii) For destructive interference: When the trough of one wave overlaps with the crest of another wave, their amplitudes “cancel” each other and we get destructive interference as shown in figure (b). The resultant amplitude is nearly zero. The destructive interference occurs if there is minimum intensity at that point, which means cos φ = – 1 ⇒ φ = π, 3π, 5π,… = (2 n-1) π, where n = 0,1,2,…. i.e. This is the phase difference in which two waves overlap to give destructive interference. Therefore,
\(I_{\text {maximum }}=(\sqrt{I_{1}}+\sqrt{I_{2}})^{2}=\left(A_{1}+A_{2}\right)^{2}\)

Hence, the resultant amplitude
A= |A₁ – A₂|

(b) Define adiabatic process. Derive an expression for work done in an adiabatic process.
Answer:
Adiabatic process: This is a process in which no heat flows into or out of the system (Q = 0). But the gas can expand by spending its internal energy or gas can be compressed through some external work. So the pressure, volume and temperature of the system may change in an adiabatic process.

For an adiabatic process, the first law becomes ΔU = W.

This implies that the work is done by the gas at the expense of internal energy or work is done on the system which increases its internal energy.

Work done in an adiabatic process: Consider μ moles of an ideal gas enclosed in a cylinder having perfectly non conducting walls and base. A frictionless and insulating piston of cross sectional area A is fitted in the cylinder.

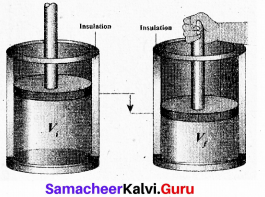
Let W be the work done when the system goes from the initial state (P_i, V_i, T_i) to the final state (P_f, V_f, T_f) adiabatically.
\(\mathrm{W}=\int_{V_{1}}^{V_{f}} \mathrm{P} d \mathrm{V}\)

By assuming that the adiabatic process occurs quasi-statically, at every stage the ideal gas law is valid. Under this condition, the adiabatic equation of state is P_Vr = Constant (or)

\(P=\frac{\text { Constant }}{\mathrm{V} r}\)
can be substituted in the equation (1), we get

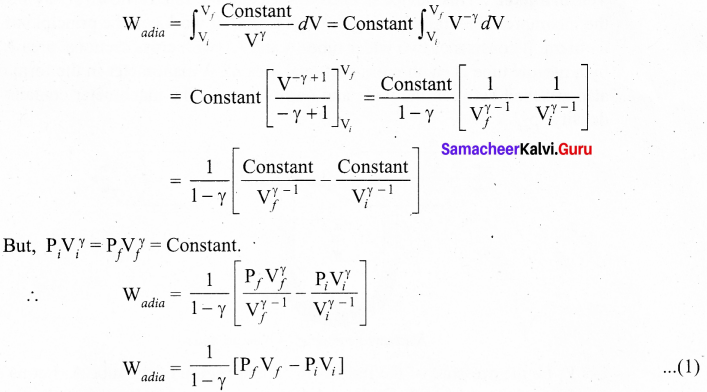
From ideal gas law, P_f V_f = μRT_f  and P_i V_i = μRT_i
Substituting in equation (2), we get
∴ W_adia = \(\frac{\mu \mathrm{R}}{\gamma-1}\) [T_f – T_i].

In adiabatic expansion, work is done by the gas. i.e., Watfoj is positive. As T_i > T_f, the gas cools during adiabatic expansion.

In adiabatic compression, work is done on the gas. i.e., Wadia is negative. As T_i < T_f, the temperature of the gas increases during adiabatic compression.

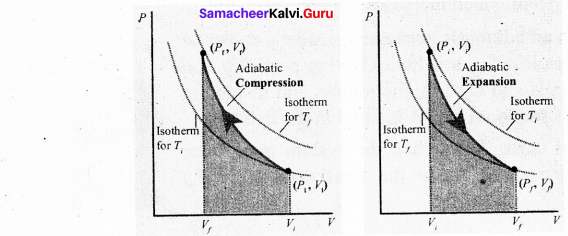
PV diagram -Work done in the adiabatic process

To differentiate between isothermal and adiabatic curves in PV diagram, the adiabatic curve is drawn along with isothennal curve for and T_f and T_i Note that adiabatic curve is steeper than isothermal curve. This is because ϒ > 1 always.

Question 38.
(a) Describe the construction and working of venturimeter and obtain an equation for the volume of liquid flowing per second though a wider entry of the tube.
Answer:
Venturimeter : This device is used to measure the rate of flow (or say flow speed) of the incompressible fluid flowing through a pipe. It works on the principle of Bernoulli’s theorem. It consists of two wider tubes A and A’ (with cross sectional area A) connected by a narrow tube B (with cross sectional area a). A manometer in the form of U-tube is also attached between the wide and narrow tubes. The manometer contains a liquid of density ‘p_m‘

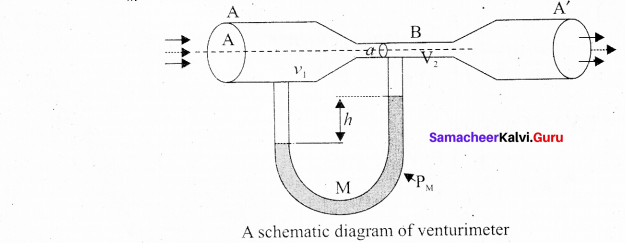
Let P₁ be the pressure of the fluid at the wider region of the tube A. Let us assume that the fluid of density ‘p’ flows from the pipe with speed ‘v₁’ and into the narrow region, its speed increases to ‘v₂’. According to the Bernoulli’s equation, this increase in speed is accompanied by a decrease in the fluid pressure P₂ at the narrow region of the tube B. Therefore, the pressure difference between the tubes A and B is noted by measuring the height difference (ΔP = P₁ – P₂) between the surfaces of the manometer liquid.

From the equation of continuity, we can say that Av₁ = av₂ which means that
\(v_{2}=\frac{\mathrm{A}}{a} v_{1}\)

Using Bernoulli’s equation,

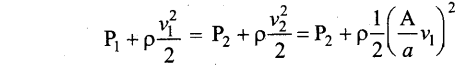
From the above equation, the pressure difference

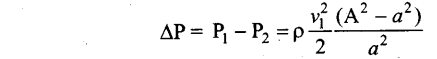
Thus, the speed of flow of fluid at the wide end of the tube A

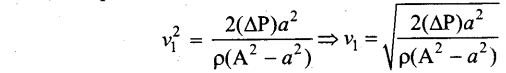
The volume of the liquid flowing out per second is

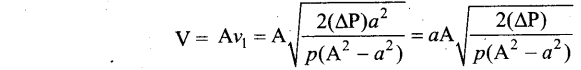
[OR]

(b) Define gravitational potential energy and derive the expression for it.
Answer:
Gravitational potential energy: Potential energy of a body at a point in a gravitational field is the work done by an external agent in moving the body from infinity to that point.

Expression for Gravitational potential energy: The gravitational force is a conservative force and hence we can define a gravitational potential energy associated with this conservative force field.

Two masses m₁ and m₂ are initially separated by a distance r’. Assuming m₁, to be fixed in its position, work must be done on m₂ to move the distance from r’ to r.

To move the mass m₂ through an infinitesimal displacement \(d \vec{r}\) from \(\vec{r}\) to \(\vec{r}\) + \(d \vec{r}\), work has to be done externally. This infinitesimal work is given by
\(d \mathrm{W}=\overrightarrow{\mathrm{F}}_{e x t} \cdot d \vec{r}\) ……………(1)

The work is done against the gravitational force, therefore,
\(\overrightarrow{\mathbf{F}}_{e x t}=\frac{\mathrm{G} m_{1} m_{2}}{r^{2}} \hat{r}\) ………………………. (2)

Substituting equation (2) in (1), we get

Thus the total work done for displacing the particle from r’ to r is f’

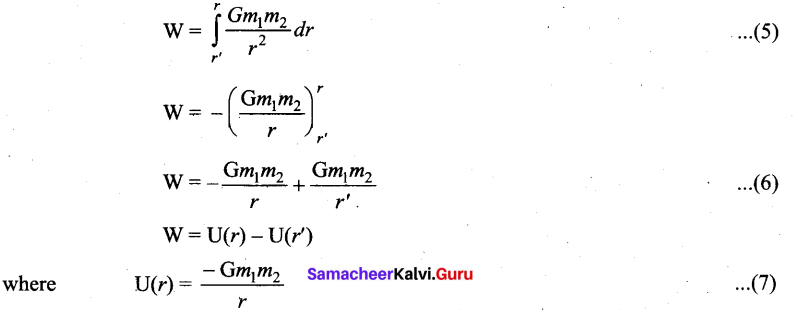
This work done W gives the gravitational potential energy difference of the system of masses m₁ and m₂ when the separation between them are r and r’ respectively.

Case 1: If r < r’ : Since gravitational force is attractive, m₂ is attracted by m₁. Then m₂ can move from r to r’ without any external work. Here work is done by the system spending its internal energy and hence the work done is said to be negative.

Case 2: If r > r’ : Work has to be done against gravity to move the object from r’ to r. Therefore work is done on the body by external force and hence work done is positive.