Tamil Nadu 11th Physics Model Question Paper 5 English Medium

Students can Download Tamil Nadu 11th Physics Model Question Paper 5 English Medium Pdf, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Physics Model Question Paper 5 English Medium

Instructions:

1. The question paper comprises of four parts
2. You are to attempt all the parts. An internal choice of questions is provided wherever: applicable
3. All questions of Part I, II, III, and IV are to be attempted separately
4. Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
6. Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
7. Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.

Time: 3 Hours
Max Marks: 70

PART – I

Answer all the questions. [15 × 1 = 15]

Question 1.
The moment of inertia of a disc of mass M and radius R about an axis which is tangential to the circumference of the disc and parallel to the diameter is……….
(a) \(\frac{5}{4}\) MR²
(b) \(\frac{3}{2}\) MR²
(c) \(\frac{4}{5}\) MR²
(d) \(\frac{2}{3} \)MR²
Answer:
(a) \(\frac{5}{4}\) MR²

Question 2.
A swimmer’s speed in the direction of flow of river is 16 km h^-1. Against the direction of flow of river, the swimmer’s speed is 8 km h^-1. The swimmer’s speed in still water and the velocity of flow of the river respectively are……….
(a) 12 km h^-1, 4 km h^-1
(b) 4 km h^-1, 12 km h^-1
(c) 24 km h^-1, 16 km h^-1
(d) 16 km h^-1, 24 km h^-1
Answer:
(a) 12 km h^-1, 4 km h^-1
Hint:
According to the question u + v = 16 and u – v = 8
By solving, we get the speed of swimmer in still water, u = 12 km h^-1
Speed of flow of river, v = 4 km h^-1

Question 3.
Shear modulus is zero for………
(a) solids
(b) liquids
(c) gases
(d) liquids and gases
Answer:
(c) gases

Question 4.
If the length and time period of an oscillating pendulum have errors of 1% and 2% respectively. The error in the estimation of ‘g’ is ………
(a) 1%
(b) 2%
(c) 3%
(d) 5%
Answer:
(d) 5%
Hint:
\(\frac{ΔL}{L}\) = 1% and \(\frac{ΔT}{T}\) = 2%
Now we have, T = 2π\(\sqrt{\frac{T}{g}}\); g = 4π\(\frac{L}{T^2}\)
\(\frac{Δg}{g}\) × 100 = (\(\frac{ΔL}{L}\)×100) + 2(\(\frac{ΔL}{L}\) × 100) = 1% + 2(2%)

Question 5.
A system of binary stars of masses m_A and m_B are moving is a circular orbits of radius r_A and r_B respectively. If T_A and T_B are the time periods of masses mA and mB respectively then,………
(a) T_A = T_B
(b) If m_A > m_A than T_A > T_B
(c) If r_B > r_A than T_B > T_A
(d) \(\frac{T_A}{T_B}\) = (\(\frac{r_A}{r_B}\))^3/2
Answer:
(a) T_A = T_B
Hint:
\(\frac{Gm_Am_B}{(r_A+r_B)^2}\) = \(\frac{m_Ar_A4π^2}{T_A^2}\) = \(\frac{m_Br_B4π^2}{T_A^2}\)
m_A r_A = m_B r_B ; T_A = T_B

Question 6.
The temperature of a wire is doubled. The Young’s modulus of elasticity………
(a) will also double
(b) will become four times
(c) will remain same
(d) will decrease
Answer:
(d) will decrease

Question 7.
A small sphere of radius 2 cm falls from rest in a viscous liquid. Heat is produced due to viscous force. The rate of production of heat when the sphere attains its terminal velocity is proportional to
(a) 2²
(b) 2³
(c) 2⁴
(d) 2⁵
Answer:
(d) 2⁵
Hint:
Rate of heat produced = F.V
(6πr|rv)v = bTtrirv2
(V α r²) Terminal velocity a r⁵ α 2⁵
[Here r = 2 m]

Question 8.
The equations of two waves acting in perpendicular direction are given as x = a cos (ωt + δ) and y = a cos (ωt + α) where δ = α + π/2 the resultant wave represents……….
(a) a parabola
(b) a circle
(c) an ellipse
(d) a straight line
Answer:
(d) a straight line

Question 9.
Two vibrating tunning forks produces progressive waves given by y₁ = 4 sin 500 πt and y₂ = 2 sin 506 πt where t is in seconds, number of beats produced per minute is……….
(a) 60
(b) 3
(c) 369
(d) 180
Answer:
(d) 180
Hint:
ω₁ = 2πf₁ ω₂ = 2πf₂
500 π = 2πf₁ 506 π = 2πf₂
f₁ = 250 f₂ = 253
f₂ = f₁ = 3 beats per sec and 3 × 60 = 180 beats per minute.

Question 10.
If the temperature of the wire is increased, then the young’s modulus will………
(a) remains the same
(b) decrease
(c) increase rapidly
(d) increase by very small amount
Answer:
(b) decrease

Question 11.
A light string passing over a smooth light pulley connects two blocks of masses m₁ and m₂ (vertically). If the acceleration of the system is g/8 then the ratio of the masses is
(a) 8 : 1
(b) 9 : 7
(c) 4 : 3
(d) 5 : 3
Answer:
(b) 9 : 7
Hint:
The FBD diagram, the force can be
m₂a = T – m₂g [a = \(\frac{g}{8}\)]
m₁a = m₁g – T
Adding we get, (m₁ + m₂) a = (m₁ – m₂)g
Putting the values, we get = \(\frac{m_1}{m_2}\) = \(\frac{9}{7}\)

Question 12.
A perfect gas is contained in a cylinder kept in vacuum. If the cylinder suddenly bursts, then the temperature of the gas……..
(a) is increased
(b) becomes OK
(c) remains unchanged
(d) is decreased
Answer:
(c) remains unchanged

Question 13.
The sample of gas expands from v₁ to v₂. The amount of work done by the gas is greatest, when the expansion is, ………..
(a) adiabatic
(b) isobaric
(c) isothermal
(d) equal in all cases
Answer:
(c) isothermal

Question 14.
The magnitude of a vector is given by……….
(a) |\(\vec{A}\)| = Ax² + Ay² + Az²
(b) |\(\vec{A}\)| = (Ax² + Ay² + Az²)_1/2
(c) (A₁ + A₂ + A₃)²
(d) A₁ cos θ + A₂ cos θ + A₁ A₂ cos θ
Answer:
(b) |\(\vec{A}\)| = (Ax² + Ay² + Az²)^1/2

Question 15.
Two soap bubbles of radii in the ratio of 2 : 1. What is the ratio of excess pressure inside them?
(a) 1 : 2
(b) 1 : 4
(c) 2 : 1
(d) 4 : 1
Answer:
(a) 1 : 2
Hint:

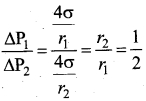
PART – II

Answer any six questions in which Q. No 23 is compulsory.

Question 16.
The position of an object moving along x axis is given by x = a + b² here a = 8.5 m, b = 2.5 ms^-2 and t is time in second. Calculate the velocity at t = 0 and t = 2 s and also calculate average velocity between t = 2 s and t = 4 s.
Answer:
v = \(\frac{dx}{dt}\) = \(\frac{d}{dt}\)(a + bt²) = 2bt = 5.0 t ms^-1
At, t = 0, v = 0 ms^-1 and at t = 2 s v = 10 ms^-1
Average velocity = \(\frac{x(4)-x(2)}{4-2}\) = \(\frac{a+16b-a-4b}{2}\) = 6 b = 6 × 2.5 = 15.0 ms^-1

Question 17.
Two vectors are given as \(\vec{b}\) = 2\(\hat{i}\) + 3\(\hat{j}\) + 5\(\hat{k}\) and F = 3\(\hat{i}\) – 2\(\hat{j}\) + 4\(\hat{k}\). Find the resultant vector.
Answer:

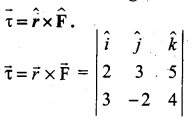
\(\vec{τ}\) = (12 -(-10))\(\hat{i}\) + (15 – 8)\(\hat{j}\) + (-4 – 9)\(\hat{k}\)
\(\vec{τ}\) = 22\(\hat{i}\) + 7\(\hat{j}\) – 13\(\hat{k}\)

Question 18.
A ball is thrown downward from a height of 30 m with a velocity of 10 ms^-1. Determine the velocity with which the ball strikes the ground by using law of conservation of energy.
Answer:
Given data:
Height from which the ball is dropped = 30 m
Velocity with which the ball is dropped = 10 ms^-1
According to law of conservation of energy,
Gain in kinetic energy = Loss in potential energy
For bodies falling down, v² = u² + 2gh
v² = (10)² + 2 × 9.8 × 30 = 688
v = 26.23 ms^-1

Question 19.
At what height, the value of g is same as at a depth of \(\frac{R}{2}\)?
Answer:
At depth = \(\frac{R}{2}\), value of acceleration due to gravity

Question 20.
Give any two applications of viscosity.
Answer:

1. The oil used as a lubricant for heavy machinery parts should have a high viscous coefficient. To select a suitable lubricant, we should know its viscosity and how it varies with temperature.
   [Note: As temperature increases, the viscosity of the liquid decreases]. Also, it helps to choose oils with low viscosity used in car engines (light machinery).
2. The highly viscous liquid is used to damp the motion of some instruments and is used as brake oil in hydraulic brakes.
3. Blood circulation through arteries and veins depends upon the viscosity of fluids.
4. Millikan conducted the oil drop experiment to determine the charge of an electron. He used the knowledge of viscosity to determine the charge.

Question 21.
An object is in uniform motion along a straight line, what will be position time graph for the motion of object, if
(i) both x₀ and v are positive |\(\vec{v}\)| is constant where x₀ is position at t = 0.
(ii) x₀ = positive, v = negative is |\(\vec{v}\)| constant.
(iii) x₀ = negative, v = positive |\(\vec{v}\)| is constant.
(iv) both x₀ and v are negative |\(\vec{v}\)| is constant.
Answer:

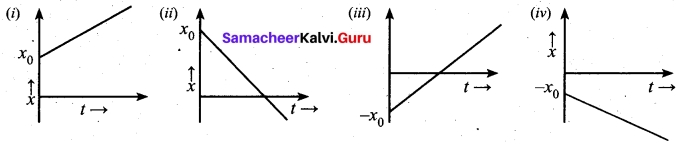
Question 22.
A sphere contracts in volume by 0.01% when taken to the bottom of sea 1 km deep. Find the bulk modulus of the material of the sphere.
Answer:
Here

Question 23.
State the second law of thermodynamics in terms of entropy.
Answer:
“For all the processes that occur in nature (irreversible process), the entropy always increases. For reversible process entropy will not change”. Entropy determines the direction in which natural process should occur.

Question 24.
What is an epoch?
Answer:
The phase of a vibrating particle corresponding to time t = 0 is called initial phase or epoch. At, t = 0, Φ = Φ₀
The constant Φ₀ is called initial phase or epoch. It tells about the initial state of motion of the vibrating particle.

PART – III

Answer any six questions in which Q.No. 29 is compulsory. [6 × 3 = 18]

Question 25.
Derive the relation between torque and angular momentum.
Answer:
We have the expression for magnitude of angular momentum of a rigid body as, L = Iω. The expression for magnitude of torque on a rigid body is, τ = Ia.
We can further write the expression for torque as,
τ = I\(\frac{dω}{dt}\) (∵α = \(\frac{dω}{dt}\))
Where, ω is angular velocity and a is angular acceleration. We can also write equation,

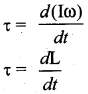
Question 26.
Discuss the properties of scalar and vector products.
Properties of vector (cross) product.
(i) The vector product of any two vectors is always another vector whose direction is perpendicular to the plane containing these two vectors, i.e., orthogonal to both the vectors \(\vec{A}\) and \(\vec{B}\) even though the vectors \(\vec{A}\) and \(\vec{B}\) may or may not be mutually orthogonal.

(ii) The vector product of two vectors is not commutative, i.e., \(\vec{A}\) × \(\vec{B}\) ≠ \(\vec{B}\) × \(\vec{A}\)
But., \(\vec{A}\) × \(\vec{B}\) = –[\(\vec{B}\) × \(\vec{A}\)]
Here it is worthwhile to note that |\(\vec{A}\) × \(\vec{B}\)| = |\(\vec{B}\) × \(\vec{A}\)| = AB sin θ i.e., in the case of the product vectors \(\vec{A}\) × \(\vec{B}\) and \(\vec{B}\) × \(\vec{A}\), the magnitudes are equal but directions are opposite to each other.

Properties of scalar product:

1. The product quantity \(\vec{A}\).\(\vec{B}\) is always a scalar. It is positive if the angle between the vectors is acute (i.e., < 90°) and negative if the angle-between them is obtuse (i.e. 90°< θ < 180°).
2. The scalar product is commutative, i.e. \(\vec{A}\).\(\vec{B}\) = \(\vec{B}\).\(\vec{A}\).
3. The vectors obey distributive law i.e. \(\vec{A}\)(\(\vec{B}\) + \(\vec{C}\)) = \(\vec{A}\).\(\vec{B}\) + \(\vec{A}\).\(\vec{C}\).
4. The angle between the vectors θ = cos^-1 (\(\frac{\vec{A}.\vec{B}}{AB}\))

Question 27.
A block of mass m slides down the plane inclined at an angle 60° with an acceleration g/2. Find the co-efficient of kinetic friction.
Answer:
Kinetic friction comes to play as the block is moving on the surface.
The forces acting on the mass are the normal force perpendicular to surface, downward gravitational force and kinetic friction f_k along the surface.
Along the x-direction.

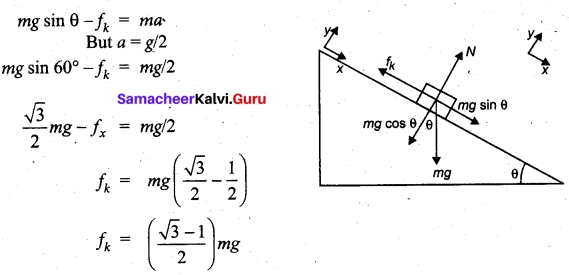
There is no motion along the y-direction as normal force is exactly balanced by the mg cos θ.
mg cos θ = N mg/2

Question 28.
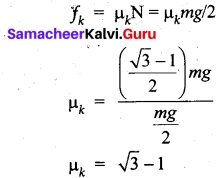
Write a note on work done by a variable force?
Answer:

When the component of a variable force F acts on a body, the small work done (dW) by the force in producing a small displacement dr is given by the relation
dW = F cos θ dr [F cos θ is the component of the variable force F] .
where, F and θ are variables. The total work done for a displacement from initial position r_i. to final position r_f is given by the relation,
\(\int_{\eta}^{r_{f}} d \mathrm{W}=\int_{r_{i}}^{r_{f}} \mathrm{F} \cos \theta dr\)
A graphical representation of the work done by a variable force is shown in figure given below. The area under the graph is the work done by the variable force.

Question 29.
Why do we have seasons on Earth?
Answer:
The common misconception is that ‘Earth revolves around the Sun, so when the Earth is very far away, it is winter and when the Earth is nearer, it is summer’. Actually, the seasons in the Earth arise due to the rotation of Earth around the Sun with 23.5° tilt. Due to this 23.5° tilt, when the northern part of Earth is farther to the Sun, the southern part is nearer to the Sun. So when it is summer in the northern hemisphere, the southern hemisphere experience winter.

Question 30.
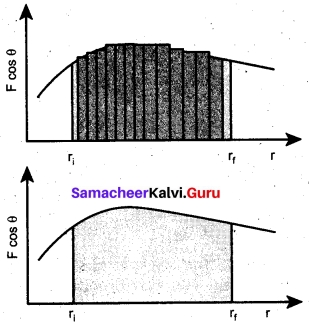
Obtain an expression for the excess of pressure inside a liquid drop.
Answer:
Excess of pressure inside air bubble in a liquid: Consider an air bubble of radius R inside a liquid having surface tension T. Let P₁ and P₂ be the pressures outside and inside the air bubble, respectively. Now, the excess pressure inside the air bubble is AP = P₁ – P₂.

In order to find the excess pressure inside the air bubble, let us consider the forces acting on the air bubble. For the hemispherical portion of the bubble, considering the forces acting on it, we get,

(i) The force due to surface tension acting towards right around the rim of length 2πR is F_T = 2πRT
(ii) The force due to outside pressure P₁ is to the right acting across a cross sectional area of πR² is F_p1 = P₁πR²
(iii) The force due to pressure P₂ inside the bubble, acting to the left is F_p2 = P₂πR².
As the air bubble is in equilibrium under the action of these forces, F_p2 = F_T + F_p1
P₂πR² = 2πRT + P₁πR² ⇒ (P₁ – P₂)πR² = 2πRT
Excess pressure is ΔP = P₂ – P₁ = \(\frac{2T}{R}\)

Question 31.
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
Answer:
T = 2π\(\sqrt{\frac{R}{g}}\)
Oscillations of a particle dropped in a tunnel along the diameter of the earth:
Consider earth to be a sphere of radius R and centre O. A straight tunnel is dug along the diameter of the earth. Let lg’ be the value of acceleration due to gravity at the surface of the Earth.

Suppose a body of mass ‘m’ is dropped into the tunnel and it is at point R i.e., at a depth d below the surface of the earth at any instant.
If g’ is acceleration due to gravity at P.
then g’ = g(1 – \(\frac{d}{R}\)) = g(\(\frac{R-d}{R}\))
If y is distence of the body from the centre of the earth then,

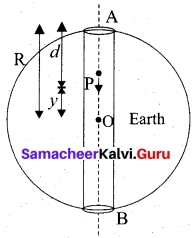
R – d = y
∴ g’ = g(\(\frac{y}{R}\))
Force acting on the body a point p is
F= -mg’ = –\(\frac{mg}{R}\) y i.e.,F α y
Negative sign indicates that the force acts in the opposite direction of displacement.
Thus the body will execute SHM with force constant,
k = \(\frac{mg}{R}\)
The period of oscillation of the body will be

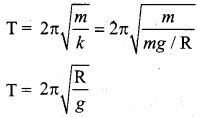
Question 32.
Which of the following represents simple harmonic motion.,
(a) x = A sin ωt + B cos 2 ωt
(b) λ = Ae^lωt
(c) x = A ln ωt
Answer:
(a) x = A sin ωt + B cos 2 ωt

This differential equation is not like the differential equation of a SHM. Therefore, x = A sin ωt + B cos 2ωt does not represent SHM.

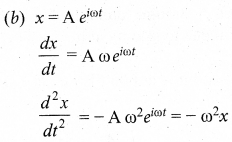
This differential equation is like the differential equation of SHM. Therefore, x = Ae^lωt represents SHM.

(c) x = A ln ωt

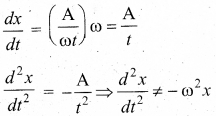
This differential equation is not like the differential equation of a SHM. Therefore, x = A In ωt does not represent SHM.

Question 33.
Obtain an expression for the excess of pressure inside a liquid drop.
Answer:
Excess pressure inside the liquid drop: Consider a liquid drop of radius R and the surface tension of the liquid is T.
The various forces acting on the liquid drop are:
(i) Force due to surface tension F_T = 2πRT towards right.
(ii) Force due to outside pressure F_p1 = P₁πR² towards right.
(iii) Force due to inside pressure F_p2 = P₂πR² towards left.

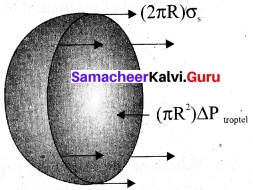
As the drop is in equilibrium, F_p2 = F_T = F_p1
P₂πR² = 2πRT + P₁πR² ⇒ (P₂ – P₁)πR² = 2πRT
Excess pressure is ΔP = P₂ – P₂ = \(\frac{2T}{R}\)

PART – IV

Answer all the questions. [5 x 5 = 25]

Question 34 (a).
Explain in detail the idea of weightlessness using lift as an example.
Answer:
When a man is standing in the elevator, there are two forces acting on him.
1. Gravitational force which acts downward. If we take the vertical direction as positive y direction, the gravitational force acting on the man is \(\vec{F}_G\)G = – mg\(\hat{j}\)
2. The normal force exerted by floor on the man which acts vertically upward, \(\vec{N}\) = N\(\hat{j}\)

Weightlessness of freely falling bodies: Freely falling objects experience only gravitational force. As they fall freely, they are not in contact with any surface (by neglecting air friction). The normal force acting on the object is zero. The downward acceleration is equal to the acceleration due to the gravity of the Earth, i.e., (a = g)

Newton’s 2nd law acting on the man N = m(g – a) [∵a = g] N = 0.

[OR]

(b) How will you determine the velocity of sound using resonance air column apparatus?
Answer:
The resonance air column apparatus is one of the simplest techniques to measure the speed of sound in air at room temperature. It consists of a cylindrical glass tube of one meter length whose one end A is open and another end B is connected to the water reservoir R through a rubber tube as shown in figure. This cylindrical glass tube is mounted on a vertical stand with a scale attached to it. The tube is partially filled with water and the water level can be adjusted by raising or lowering the water in the reservoir R. The surface of the water will act as a closed end and other as the open end.

Therefore, it behaves like a closed organ pipe, forming nodes at the surface of water and antinodes at the closed end. When a vibrating tuning fork is brought near the open end of the tube, longitudinal waves are formed inside the air column. These waves move downward as shown in Figure, and reach the surfaces of water and get reflected and produce standing waves. The length of the air column is varied by changing the water level until a loud sound is produced in the air column. At this particular length the frequency of waves in the air column resonates with the frequency of the tuning fork (natural frequency of the tuning fork). At resonance, the frequency of sound waves produced is equal to the frequency of the tuning fork. This will occur only when the length of air column is proportional to (\(\frac{1}{4}\))^th of the wavelength of the sound waves produced. Let the first resonance occur at length L₁ then

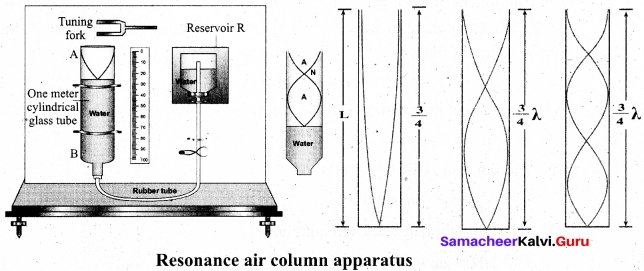
\(\frac{1}{4}\)λ = L₁ ……..(1)
But since the antinodes are not exactly formed at the open end, we have to include a correction, called end correction e, by assuming that the antinode is formed at some small distance above the open end. Including this end correction, the first resonance is
\(\frac{1}{4}\)λ = L₁ + e …….(2)
Now the length of the air column is increased to get the second resonance. Let L₂ be the length at which the second resonance occurs. Again taking end correction into account, we have
\(\frac{3}{4}\)λ = L₂ + e ……..(3)
In order to avoid end correction, let us take the difference of equation (2) and equation (1), we get \(\frac{3}{4}\)λ – \(\frac{1}{4}\)λ = (L₂ + e) – (L₁ + e) ⇒ \(\frac{1}{2}\)λ, = L₂ – L₁ = ΔL ⇒ λ = 2ΔL
The speed of the sound in air at room temperature can be computed by using the formula
v = fλ = 2fΔL
Further, to compute the end correction, we use equation (2) and equation (3), we get
e = \(\frac{L_2-3L_1}{2}\)

Question 35 (a).
Briefly explain the origin of friction. Show that in an inclined plane, angle of friction is equal to angle of repose.
Answer:
If a very gentle force in the horizontal direction is given to an object at rest on the table it does not move. It is because of the opposing force exerted by the surface on the object which resists its motion. This force is called the frictional force.

During the time of Newton and Galileo, frictional force was considered as one of the natural forces like gravitational force. But in the twentieth century, the understanding on atoms, electron and protons has changed the perspective. The frictional force is actually the electromagnetic force between the atoms on the two surfaces. Even well polished surfaces have irregularities on the surface at the microscopic level.

The component of force parallel to the inclined plane (mg sin θ) tries to move the object down. The component of force perpendicular to the inclined plane (mg cos θ) is balanced by the Normal force (N).
N = mg cos θ ……(1)
When the object just begins to move, the static friction attains its maximum value
f_s = \(f_{s}^{\max }\)
This friction also satisfies the relation
\(f_{s}^{\max }\) = µ_s sin θ ……(2)
Equating the right hand side of equations (1) and (2),
\(f_{s}^{\max }\)/N = sin θ / cos θ
From the definition of angle of friction, we also know that
tan θ = µ_s …….(3)
in which θ is the angle of friction.
Thus the angle of repose is the same as angle of friction. But the difference is that the angle of repose refers to inclined surfaces and the angle of friction is applicable to any type of surface.

[OR]

(b) Show that the minimum speed at the lowest point as \(\sqrt{5gr}\) in a vertical circle executed by the object.
Answer:
Minimum speed at the lowest point 1
To have this minimum speed (v₂ = \(\sqrt{gr}\) at point 2, the body must have minimum speed
also at point 1. By making use of equation we can find the minimum speed at point 1.
\(v_{1}^{2}-v_{2}^{2}\) = 4gr ……..(1)
Substituting equation v₂ = \(\sqrt{gr}\) in \(v_{1}^{2}-v_{2}^{2}\) = 4gr
\(v_{1}^{2}\) = 5gr
v₁ = \(\sqrt{5gr}\) …..(2)

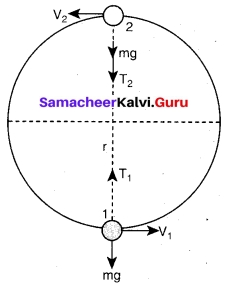
The body must have a speed at point 1, v₁ ≥ \(\sqrt{5gr}\) to stay in the circular path. From equations v₂ = \(\sqrt{gr}\) and v₁ = \(\sqrt{5gr}\), it is clear that the minimum speed at the lowest point 1 should be 5 times more than the minimum speed at the highest point 2, so that the body loops without leaving the circle.

Question 36 (a).
What are the characteristics of stationery waves? Give the laws of transverse vibrations in a stretched string.
Characteristics of stationary waves:
1. Stationary waves are characterised by the confinement of a wave disturbance between two rigid boundaries. This means, the wave does not move forward or backward in a medium (does not advance), it remains steady at its place. Therefore, they are called “stationary waves or standing waves”.
2. Certain points in the region in which the wave exists have maximum amplitude, called as anti-nodes and at certain points the amplitude is minimum or zero, called as nodes.
3. The distance between two consecutive nodes (or) anti-nodes is \(\frac{λ}{2}\).
4. The distance between a node and its neighbouring anti-node is \(\frac{λ}{4}\).
5. The transfer of energy along the standing wave is zero.

Laws of transverse vibrations in stretched strings: There are three laws of transverse vibrations of stretched strings which are given as follows:
(i) The law of length: For a given wire with tension T (which is fixed) and mass per unit length µ (fixed) the frequency varies inversely with the vibrating length. Therefore,
f ∝ \(\frac{1}{l}\) ⇒ f = \(\frac{c}{l}\)
⇒ l × f = C, where C is a constant

(ii) The law of tension: For a given vibrating length l (fixed) and mass per unit length µ (fixed) the frequency varies directly with the square root of the tension T.
f ∝ √T
⇒ A√T, where A is constant

(iii) The law of mass: For a given vibrating length l (fixed) and tension T (fixed) the frequency varies inversely with the square root of the mass per unit length µ.
f ∝ \(\frac{1}{√µ}\)
⇒ f = \(\frac{B}{√µ}\) where B is constant

[OR]

(b) Define isothermal process. Derive an expression for work done in isothermal process.
Answer:
Isothermal process:
It is a process in which the temperature remains constant but the pressure and volume of a thermodynamic system will change. The ideal gas equation is PV = µRT

Work done in an isothermal process: Consider an ideal gas which is allowed to expand quasi-statically at constant temperature from initial state (Pⁱi) to the final state (P^{f, V}f). We can calculate the work done by the gas during this process. The work done by the gas,
W = \(\int_{v_{i}}^{v_{f}} \mathrm{p} d \mathrm{v}\) ……(1)
As the process occurs quasi-statically, at every stage the gas is at equilibrium with the surroundings. Since it is in equilibrium at every stage the ideal gas law is valid. Writing pressure in terms of volume and temperature,
P = \(\frac{µRT}{V}\) …….(2)
Substituting equation (2) in (1) we get

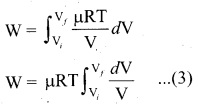
In equation (3), we take µRT out of the integral, since it is constant throughout the isothermal process.
By performing the integration in equation (3), we get
W = µRT ln (\(\frac{V_f}{V_i}\)) …….(4)
Since we have an isothermal expansion, \(\frac{V_f}{V_i}\) < 1, so ln (\(\frac{V_f}{V_i}\)) < 0 As a result the work done by the gas during an isothermal expansion is positive.
The above result in equation (4) is true for isothermal compression also. But in an isothermal compression \(\frac{V_f}{V_i}\) < 1, so ln (\(\frac{V_f}{V_i}\)) < 0
As a result the work done on the gas in an isothermal compression is negative.
In the PV diagram the work done during the isothermal expansion is equal to the area under the graph.

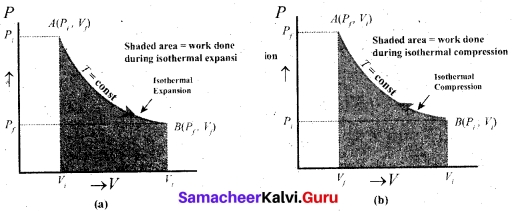
Similarly for an isothermal compression, the area under the PV graph is equal to the work done on the gas which turns out to be the area with a negative sign.

Question 37 (a).
Convert a velocity of 72 km h^-1 into ms^-1 with the help of dimensional analysis.
Answer:
n₁ = 72 km h^-1 n₂ = ? ms^-1
L₁ = 1 km L₂ = 1 m
T₁ = lh T₂ = 1S

[OR]

(b) convert
(i) 3 m.s^-2 to km h^-2
(ii) G = 6.67 × 10^-11 N m² kg^-2 to cm³ g^-1 s^-2
Answer:

= 3.8880 × 10⁴ km h^-2 = 3.9 ×. 10⁴ km h^-2

(ii) G = 6.67 × 10^-11 Nm² kg^-2
= 6.67 × 10^-11 (kg m s^-2) (m² kg^-2)
= 6.67 × 10^-11 kg^-1 m³ s^-2
= 6.67 × 10^-11 (1000 g)^-1 (100 cm)³ (s^-2)
= 6.67 × 10^-11 × \(\frac{1}{1000}\) × 100 × 100 × 100 g^-1 cm³ s^-2
= 6.67 × 10^-8 g^-1 cm³ s^-2

Question 38 (a)
(i) A uniform sphere of mass 200 g rotates on a horizontal surface without shipping. If centre of the sphere moves with a velocity 2.00 cm/s then its kinetic energy is?
As the sphere rolls without slipping on the plane surface, it’s angular speed about the center is w = \(\frac{v_{\mathrm{CM}}}{r}\)
kinetic energy,

(ii) Derive the expression for kinetic energy in rotating object and also derive the relation between rotational kinetic energy and angular momentum.
Let us consider a rigid body rotating with angular velocity co about an axis as shown in figure. Every particle of the body will have the same angular velocity co and different tangential velocities v based on its positions from the axis of rotation.

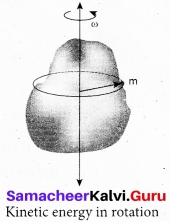
Let us choose a particle of mass m_i situated at distance r_i. from the axis of rotation. It has a tangential velocity v_i given by the relation, v_i = r_i ω. The kinetic energy KE_i of the particle is,
KE_i = \(\frac { 1 }{ 2 }\) m_iv_i²
writing the expression with the angular velocity,
KE = \(\frac { 1 }{ 2 }\) m_i(r_iω)² = \(\frac { 1 }{ 2 }\) (m_ir_i²)ω²
For the kinetic energy of the whole body, which is made up of large number of such particles, the equation is written with summation as,
KE = \(\frac { 1 }{ 2 }\)(∑ m_ir_i²)w²
where, the term ∑ m_ir_i²) is the moment of inertia I of the whole body. ∑ m_ir_i²)
Hence, the expression for KE of the rigid body in rotational motion is,
KE = \(\frac { 1 }{ 2 }\)Iω²
This is analogous to the expression for kinetic energy in translational motion.
KE = \(\frac { 1 }{ 2 }\)Mv²

Relation between rotational kinetic energy and angular momentum:
Let a rigid body of moment of inertia I rotate with angular velocity w.
The angular momentum of a rigid body is, L = I ω
The rotational kinetic energy of the rigid body is, KE = \(\frac { 1 }{ 2 }\)I w²
By multiplying the numerator and denominator of the above equation with I, we get a relation between L and KE as,
KE =\(\frac { 1 }{ 2 }\) \(\frac{I^{2} \omega^{2}}{I}\) = \(\frac { 1 }{ 2 }\)\(\frac{(\mathrm{I} \omega)^{2}}{\mathrm{I}}\)

[OR]

(b) what is a sonometer? Give its construction and working. Explain how to determine the frequency of tuning fork using sonometer.
Answer:
Stationary waves in sonometer:
Sono means sound related, and sonometer implies sound – related measurements. It is a device for demonstrating the relationship between the frequency of the sound produced in the transverse standing wave in a string, and the tension, length and mass per unit length of the string. Therefore, using this device, we can determine the following quantities:

the frequency of the tuning fork or frequency of alternating current the tension in the string the unknown hanging mass.

Construction:
The sonometer is made up of a hollow box which is one meter long with a uniform metallic thin string attached to it. One end of the string is connected to a hook and the other end is connected to a weight hanger through a pulley as shown in figure. Since only one string is used, it is also known as monochord. The weights are added to the free end of the wrire to increase the tension of the wfire. Two adjustable wooden knives are put over the board, and their positions are adjusted to change the vibrating length of the stretched wire.

working:
A transverse stationary or standing wave is produced and hence, at the knife edges P and Q, nodes are formed. In between the knife edges, anti-nodes are formed. If the length of the vibrating element is l then
l = \(\frac { λ }{ 2 }\) ⇒ λ = 2l
Let f be the frequency of the vibrating element, T the tension of in the string and µ the mass per unit length of the string. Then using equation ,we get
ƒ = \(\frac { v }{ λ}\) = \(\frac { 1 }{ 2l }\)\(\sqrt{\frac{T}{\mu}}\)
Let p be the density of the material of the string and d be the diameter of the string. Then the mass per unit length µ,
µ = Area x density = πr²p = \(\frac{\pi \rho d^{2}}{4}\)