Students can Download Tamil Nadu 11th Physics Previous Year Question Paper March 2019 English Medium Pdf, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 11th Physics Previous Year Question Paper March 2019 English Medium
Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III and IV are to be attempted separately.
- Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer.
- Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
- Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
- Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.
Time: 2½ Hours
Max Marks: 70
PART – I
Answer all the Questions. [15 × 1 = 15]
Question 1.
Which graph represents uniform acceleration?
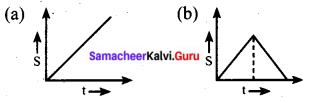
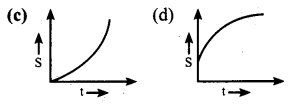
Answer:
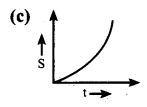
Question 2.
A body of mass 5 kg is thrown up vertically with a kinetic energy of 1000 J. If acceleration due to gravity is 10 ms-2, find the height at which the kinetic energy becomes half of the original value.
(a) 10 m
(b) 20 m
(c) 50 m
(d) 100 m
Answer:
(a) 10 m
Half KE is converted into potential energy.
Then PE = \(\frac{1}{2}\) KE
mgh = \(\frac{1000}{2}\) = 500
\(\mathrm{h}=\frac{500}{\mathrm{mg}}=\frac{500}{5 \times 10}=10 \mathrm{m}\)
![]()
Question 3.
The process in which heat transfer is by actual movement of molecules in fluids such as liquids and gases is called ________
(a) Thermal conductivity
(b) Convection
(c) Conduction
(d) Radiation
Answer:
(b) Convection
Question 4.
If the temperature of the wire is increased, then Young’s Modules will
(a) increase rapidly
(b) increase by a very small amount
(c) remain the same
(d) decrease
Answer:
(d) decrease
Question 5.
The amplitude and time period of a simple pendulum bob are 0.05 m and 2s respectively. Then the maximum velocity of the bob is :
(a) 0.157 ms-1
(b) 0.257 ms-1
(c) 0.10 ms-1
(d) 0.025 ms-1
Answer:
(a) 0.157 ms-1

Question 6.
There is a small bubble at one end and a bigger bubble at another end of a pipe. Which among the following will happen?

(a) remains in equilibrium
(b) smaller will grow until they collapse
(c) bigger will grow until they collapse
(d) none of the above
Answer:
(b) smaller will grow until they collapse
Excess pressure is \(\Delta P=P_{2}-P_{1}=\frac{4 T}{R}\)
![]()
Question 7.
A closed cylindrical container is partially filled with water. As the container rotates in a horizontal plane above a perpendicular bisector, its moment of inertia :
(a) remains constant
(b) depends on the direction of rotation
(c) increases
(d) decreases
Answer:
(c) increases
Question 8.
Which of the following represents a wave?
(a) \(\frac{1}{(x+v t)}\)
(b) sin (x + vt)
(c) (x – vt)3
(d) x(x + vt)
Answer:
(b) sin (x + vt)
Question 9.
Which of the following pairs of physical quantities have the same dimension?
(a) Torque and Power
(b) Force and Torque
(c) Force and Power
(d) Torque and Energy
Answer:
(d) Torque and Energy
Question 10.
If the internal energy of an ideal gas U and volume V are doubled then the pressure of the gas _______
(a) halves
(b) quadruples
(c) doubles
(d) remains the same
Answer:
(d) remains the same
![]()
Question 11.
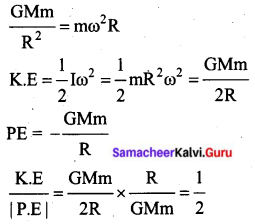
For a satellite moving in an orbit around the earth, the ratio of kinetic energy to potential energy is:
(a) 2
(b) √2
(c) \(\frac { 1 }{ 2 }\)
(d) \(\frac{1}{\sqrt{2}}\)
Answer:
(c) \(\frac { 1 }{ 2 }\)
Question 12.
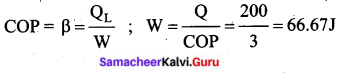
A refrigerator has a COP of 3. How much work must be supplied to a refrigerator in order to remove 200 J of heat from its interior?
(a) 33.33 J
(b) 44.44 J
(c) 66.67 J
(d) 50 J
Answer:
(c) 66.67 J
Question 13.
If the linear momentum of the object is increased by 0.1 % then the kinetic energy is increased by:
(a) 0.4 %
(b) 0.01 %
(c) 0.1 %
(d) 0.2 %
Answer:
(d) 0.2 %

Question 14.
What is the angular displacement made by a particle after 5s, when it starts from rest with an angular acceleration of 0.2 rads-2?
(a) 4 rad
(b) 1 rad
(c) 2.5 rad
(d) 5 rad
Answer:
(c) 2.5 rad
From the equation of circular motion, ω = 0
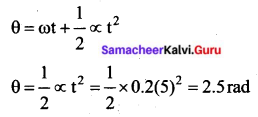
Question 15.
In an isochoric process, find which is relevant among the following :
(a) ΔU = 0
(b) ΔT = 0
(c) W = 0
(d) Q = 0
Answer:
(c) W = 0
![]()
PART – II
Answer any six of the following questions. Q. No. 24 is compulsory. [6 × 2 = 12]
Question 16.
Write any two errors of systematic errors. Explain them.
Answer:
Systematic errors: Systematic errors are reproducible inaccuracies that are consistently in the same direction. These occur often due to a problem that persists throughout the experiment. Systematic errors can be classified as follows.
- Instrumental errors: When an instrument is not calibrated properly at the time of manufacture, instrumental errors may arise. If a measurement is made with a meter scale whose end is worn out, the result obtained will have errors. These errors can be corrected by choosing the instrument carefully.
- Personal errors: These errors are due to individuals performing the experiment, maybe due to incorrect initial setting up of the experiment or carelessness of the individual making the observation due to improper precautions.
Question 17.
What is a projectile? Give two examples.
Answer:
Projectile: When an object is thrown in the air with some initial velocity and then allowed to move under the action of gravity alone, the object is known as a projectile.
Example:
- A bullet fired from a rifle.
- A ball is thrown in any direction
Question 18.
State Newton’s Second Law of Motion.
Answer:
The force acting on an object is equal to the rate of change of its momentum
\(\overrightarrow{\mathrm{F}}=\frac{d \vec{p}}{d t}\)
![]()
Question 19.
A car takes a turn with the velocity 50 ms-1 on a circular road of the radius of curvature
10 m. Calculate the centrifugal force experienced by a person of mass 60 kg inside the car.
Answer:
Given: Mass of a person = 60 kg
Velocity of the car = 50 ms-1
Radius of curvature = 10 m
Centrifugal force
\(\mathrm{F}=\frac{m \mathrm{V}^{2}}{r}=\frac{60 \times(50)^{2}}{10}=15,000 \mathrm{N}\)
Question 20.
Why is it more difficult to revolve a stone tied it to a longer string than a stone tied to a shorter string?
Answer:
MI of stone I = ml2 (l = length of string) l is large, α is very small
\(\begin{array}{l}
\tau=I \alpha \\
\alpha=\frac{\tau}{I}=\frac{\tau}{m l^{2}}
\end{array}\)
if l is large α is very small.
∴ more difficult to revolve.
Question 21.
State Stefan-Boltzmann law and write its expression.
Answer:
Stefan Boltzmann law states that the total amount of heat radiated per second per unit area of a black body is directly proportional to the fourth power of its absolute temperature.
E ∝ T4 (or) E = σT4
Question 22.
List the factors affecting Brownian motion.
Answer:
- Brownian motion increases with increasing temperature.
- Brownian motion decreases with bigger particle size, high viscosity and density of the liquid (or) gas.
Question 23.
“Soldiers are not allowed to march on a bridge.” Give reason.
Answer:
While crossing a bridge, if the period of stepping on the ground by marching soldiers be equal to the natural frequency of the bridge, it may be thrown into resonance vibration and the vibrations may be so large that the bridge may collapse. Thus to avoid resonant vibration of the bridge. Soldiers are ordered to break steps.
![]()
Question 24.
The surface tension of a soap solution is 0.03 Nm-1. How much work is done in producing soap bubble of radius 0.05 m?
Answer:
Surface area (∆s) = 4πr2 = 4 × 3.14 × (0.05)2
∆s = 0.0314 m
No. of surface area of a soap bubble = 2 (outer and inner area)
Total surface energy (E) = 2T∆S = 2 × 0.03 × 0.0314
E = 0.0018 J
PART – III
Answer any six of the following questions. Q. No. 33 is compulsory. [6 × 3 = 18]
Question 25.
What is the torque of the force \(\overrightarrow{\mathbf{F}}=3 \hat{i}-2 \hat{j}+4 \hat{k}\) acting at a point \(\vec{r}=2 \hat{i}+3 \hat{j}+5 \hat{k}\) about the origin?
Answer:
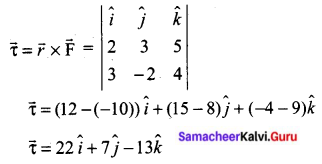
Question 26.
What are the various types of friction? Suggest a few methods to reduce friction.
Answer:
There are two types of Friction:
(i) Static Friction: Static friction is the force which opposes the initiation of motion of an object on the surface. The magnitude of static frictional force fs lies between \(0 \leq f_{s} \leq \mu_{s} N\)
where, µs — coefficient of static friction
N — Normal force
(ii) Kinetic friction: The frictional force exerted by the surface when an object slides is called kinetic friction. Also called as sliding friction or dynamic friction,
fk = µkN
where µk — the coefficient of kinetic friction
N — Normal force exerted by the surface on the object
Methods to reduce friction: Friction can be reduced
- By using lubricants
- By using Ball bearings
- By polishing
- By streamlining
![]()
Question 27.
A heavy body and a light body have the same momentum. Which one of them has more kinetic energy and why?
Answer:
Lighter body has more K.E. as K.E. = \(\frac{p^{2}}{2 m}\) and for constant p, K.E. ∝ \(\frac{1}{m}\).
The lighter body has more kinetic energy.
Question 28.
Find the rotational kinetic energy of a ring of mass 9 kg and radius 3 m rotating with 240 rpm about an axis passing through its centre and perpendicular to its plane.
Answer:
The rotational kinetic energy is, KE = \frac{1}{2} \mathrm{I} \omega^{2}
The moment of inertia of the ring is, I = MR2
I = 9 × 32 = 9 × 9 = 81 kg m2
The angular speed of the ring is,
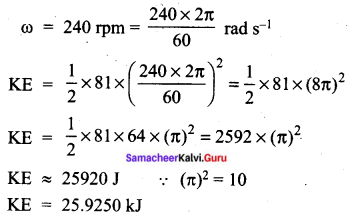
Question 29.
What do you mean by the term weightlessness? Explain the state of weightlessness of a freely falling body.
Answer:
When a man is standing in the elevator, there are two forces acting on him.
1. The gravitational force acts downward. If we take the vertical direction as positive y-direction, the gravitational force acting on the man is \(\overrightarrow{\mathrm{F}}_{\mathrm{G}}=-m g \hat{j}\)
2. The normal force exerted by the floor on the man which acts vertically upward, \(\overrightarrow{\mathrm{N}}=\mathrm{N} \hat{j}\)
The weightlessness of freely falling bodies: Freely falling objects experience only gravitational force. As they fall freely, they are not in contact with any surface (by neglecting air friction). The normal force acting on the object is zero. The downward acceleration is equal to the acceleration due to the gravity of the Earth, i.e., (a = g)
Newton’s 2nd law acting on the man N = m(g – a)
a = g
∴ N = w(g – g) = 0
![]()
Question 30.
Derive the expression for the terminal velocity of a sphere falling through a viscous liquid.
Answer:
The expression for terminal velocity: Consider a sphere of radius r which falls freely through a highly viscous liquid of coefficient of viscosity η. Let the density of the material of the sphere be ρ and the density of the fluid be σ.
The gravitational force acting on the sphere,


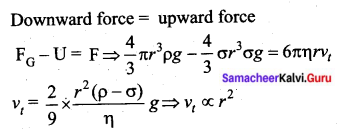
Here, it should be noted that the terminal speed of the sphere is directly proportional to the square of its radius. If σ is greater than ρ, then the term (ρ – σ) becomes negative leading to a negative terminal velocity.
Question 31.
Explain the linear expansion of solid.
Answer:
Linear Expansion: In solids, for a small change in temperature
ΔT, the fractional change in length to \(\left(\frac{\Delta L}{L_{0}}\right)\) is directly proportional to ΔT.
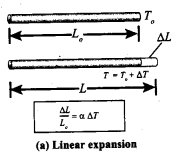
\(\frac{\Delta \mathrm{L}}{\mathrm{L}_{0}}=\alpha_{\mathrm{L}} \Delta \mathrm{T}\)
Therefore, \(\alpha_{\mathrm{L}}=\frac{\Delta \mathrm{L}}{\mathrm{L}_{0} \Delta \mathrm{T}}\)
Where, αL = coefficient of linear expansion, ΔL = Change in length, L = Original length, ΔT = Change in temperature.
Question 32.
Write down any six postulates of the kinetic theory of gases.
Answer:
- All the molecules of a gas are identical, elastic spheres.
- The molecules of different gases are different.
- The number of molecules in a gas is very large and the average separation between them is larger than size of the gas molecules.
- The molecules of a gas are in a state of continuous random motion.
- The molecules collide with one another and also with the walls of the container.
- These collisions are perfectly elastic so. that there is no loss of kinetic energy during .collisions.
- Between two successive collisions, a molecule moves with uniform velocity.
- The molecules do not exert any force of attraction or repulsion on each other except during collision. The molecules do not possess any potential energy and the energy is wholly kinetic.
- The collisions are instantaneous. The time spent by a molecule in each collision is very small compared to the time elapsed between two consecutive collisions.
- These molecules obey Newton’s laws of motion even though they move randomly.
![]()
Question 33.
Two waves of wavelength 99 cm and 100 cm both travelling with the velocity of 396 ms-1 are made to interfere. Calculate the number of beats produced by them per sec.
Answer:
λ1 = 99 cm = 0.99 m
λ2 = 100 cm = 1 m
Velocity of sound waves in a gas is v = 396 ms-1
Relation between wavelength and velocity, v = λf

PART – IV
Answer all the questions. [5 × 5 = 25]
Question 34(a).
Explain the principle of homogeneity of dimensions and derive an expression for the force F acting on a body moving in a circular path depending on the mass of the body (m), velocity (v) and radius (r) of the circular path. Obtain the expression for the force by the dimensional analysis method (take the value k = 1)
Answer:
The principle of homogeneity of dimensions states that the dimensions of all the terms in a physical expression should be the same. For example, in the physical expression v2 = u2 + 2as, the dimensions of v2, u2 and 2as are the same and equal to [L2T-2].
F ∝ ma vb rc
F = K ma vb rc
Here K = 1
∴ F = ma vb rc
Dimensionally, [MLT-2] = [M]a [LT-1]b [L]c
Compare the power of M, L and T
a = 1 ….. (1)
b + c = 1 ….. (2)
-b = -2
b = 2 …… (3)
Sub (3) in (2) we get
b + c = 1
2 + c = 1
c = -1 …… (4)
Substitute a, b and c value in force equation
F = ma vb rc = m v2 r-1
\(F=\frac{m v^{2}}{r}\)
This equation is known as centripetal force.
[OR]
Question 34(b).
State and prove Bernoulli’s theorem for a flow of incompressible, non-viscous, and streamlined flow of liquid.
Answer:
Bernoulli’s theorem: According to Bernoulli’s theorem, the sum of pressure energy, kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow remains a constant.
Mathematically, \(\frac{P}{\rho}+\frac{1}{2} v^{2}+g h=\text { constant }\)
This is known as Bernoulli’s equation.
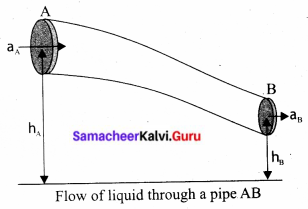
Proof: Let us consider a flow of liquid through a pipe AB. Let V be the volume of the liquid when it enters A in a time t which is equal to the volume of the liquid leaving B at the same time. Let aA, vA and PA be the area of cross-section of the tube, the velocity of the liquid and pressure exerted by the liquid at A respectively.
Let the force exerted by the liquid at A is FA = PAaA
Distance travelled by the liquid in time t is d = vAt
Therefore, the work done is W = FAd = PAaAvAt
But aAvAt = aAd = V, the volume of the liquid entering at A.
Thus, the work done is the pressure energy (at A), W = FAd = PAV
Pressure energy per unit volume at A = \(\frac{\rho_{\mathrm{A}}}{\rho_{\mathrm{B}}}=\frac{4}{3}\)
Pressure energy per unit mass at A = \(\frac{\text { Pressure energy }}{\text { Mass }}=\frac{\mathrm{P}_{\mathrm{A}} \mathrm{V}}{m}=\frac{\mathrm{P}_{\mathrm{A}}}{\frac{m}{\mathrm{V}}}=\frac{\mathrm{P}_{\mathrm{A}}}{\rho}\)
Since m is the mass of the liquid entering at A in a given time, therefore, pressure energy of the liquid at A is \(\mathrm{E}_{\mathrm{PA}}=\mathrm{P}_{\mathrm{A}} \mathrm{V}=\mathrm{P}_{\mathrm{A}} \mathrm{V} \times\left(\frac{m}{m}\right)=m \frac{\mathrm{P}_{\mathrm{A}}}{\rho}\)
Potential energy of the liquid at A,
PEA = mghA
Due to the flow of liquid, the kinetic energy of the liquid at A,
\(\mathrm{KE}_{\mathrm{A}}=\frac{1}{2} m v_{\mathrm{A}}^{2}\)
Therefore, the total energy due to the flow of liquid at A,
EA = EPA + KEA + PEA
\(E_{A}=m \frac{P_{A}}{\rho}+\frac{1}{2} m v_{A}^{2}+m g h_{A}\)
Similarly, let aB, vB and PB be the area of cross section of the tube, velocity of the liquid and pressure exerted by the liquid at B. Calculating the total energy at EB, we get

The above equation is the consequence of the conservation of energy which is true until there is no loss of energy due to friction. But in practice, some energy is lost due to friction. This arises due to the fact that in a fluid flow, the layers flowing with different velocities exert frictional forces on each other. This loss of energy is generally converted into heat energy. Therefore, Bernoulli’s relation is strictly valid for fluids with zero viscosity or non-viscous liquids. Notice that when the liquid flows through a horizontal ‘ pipe, then
\(h=0 \Rightarrow \frac{\mathrm{P}}{\rho g}+\frac{1}{2} \frac{v^{2}}{g}=\text { constant }\)
![]()
Question 35.
(a) Prove the law of conservation of momentum. Use it to find the recoil velocity of a gun when a bullet is fired from it.
Answer:
In nature, conservation laws play a very important role. The dynamics of motion of bodies can be analysed very effectively using conservation laws. There are three conservation laws in mechanics. Conservation of total energy, conservation of total linear momentum, and conservation of angular momentum. By combining Newton’s second and third laws, we can derive the law of conservation of total linear momentum.
When two particles interact with each other, they exert equal and opposite forces on each other. The particle 1 exerts force \(\overrightarrow{\mathrm{F}}_{21}\) on particle 2 and particle 2 exerts an exactly equal and opposite force \(\overrightarrow{\mathrm{F}}_{21}\) on particle 1 according to Newton’s third law.
\(\overrightarrow{\mathrm{F}_{21}}=-\overrightarrow{\mathrm{F}_{12}}\) ….. (1)
In terms of momentum of particles, the force on each particle (Newton’s second law) can be written as
\(\overrightarrow{\mathrm{F}_{12}}=\frac{d \overrightarrow{p_{1}}}{d t} \text { and } \overrightarrow{\mathrm{F}_{21}}=\frac{d \overrightarrow{p_{2}}}{d t}\)
Here \(\vec{p}_{1}\) is the momentum of particle 1 which changes due to the force \(\overrightarrow{\mathrm{F}_{12}}\) exerted by particle 2. Further \(\vec{p}_{2}\) is the momentum of particle 2. This changes due to \(\overrightarrow{\mathrm{F}_{21}}\) exerted by particle 1.
Substitute equation (2) in equation (1)
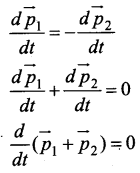
It implies that \(\overrightarrow{p_{1}}+\overrightarrow{p_{2}}\) = constant vector (always).
\(\overrightarrow{p_{1}}+\overrightarrow{p_{2}}\) is the total linear momentum of the two particles (\(\overrightarrow{p_{\text {tot}}}=\overrightarrow{p_{1}}+\overrightarrow{p_{2}}\)). It is also called as total linear momentum of the system. Here, the two particles constitute the system. From this result, the law of conservation of linear momentum can be stated as follows.
If there are no external forces acting on the system, then the total linear momentum of the system (\(\vec{P}_{t o t}\)) is always a constant vector. In otherwords, the total linear momentum of the system is conserved in time. Here the word ‘conserve’ means that \(\overrightarrow{p_{1}}\) and \(\overrightarrow{p_{2}}\) can vary, in such a way that \(\overrightarrow{p_{1}}+\overrightarrow{p_{2}}\) is a constant vector.
The forces \(\overrightarrow{\mathrm{F}}_{12}\) and \(\overrightarrow{\mathrm{F}}_{21}\) are called the internal forces of the system, because they act only between the two particles. There is no external force acting on the two particles from outside. In such a case the total linear momentum of the system is a constant vector or is conserved.
Meaning of law of conservation of momentum:
1. The Law of conservation of linear momentum is a vector; law. It implies that both the magnitude and direction of total linear momentum are constant. In some cases, this total momentum can also be zero.
2. To analyse the motion of a particle, we can either use Newton’s second law or the law of conservation of linear momentum. Newton’s second law requires us to specify the forces involved in the process. This is difficult to specify in real situations. But conservation of linear momentum does not require any force involved in the process. It is convenient and hence important.
For example, when two particles collide, the forces exerted by these two particles on each other is difficult to specify. But it is easier to apply conservation of linear momentum during the collision process.
Examples:
Consider the firing of a gun. Here the system is Gun+bullet. Initially, the gun and bullet are at rest, hence the total linear momentum of the system is zero. Let \(\overrightarrow{\mathrm{P}}_{1}\) be the momentum of the bullet and \(\overrightarrow{\mathrm{P}}_{2}\) be the momentum of the gun before firing. Since initially both are at rest,
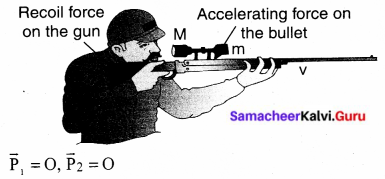
Total momentum before firing the gun is zero, \(\vec{p}_{1}+\vec{p}_{2}=0\)
According to the law of conservation of linear momentum, total linear momentum has to be zero after the firing also.
When the gun is fired, a force is exerted by the gun on the bulletin forward direction. Now the momentum of the bullet changes from \(\vec{p}_{1}+\vec{p}_{1}^{\prime}\). To conserve the total linear momentum of the system, the momentum of the gun must also change from \(\vec{p}_{2}\) to \(\vec{p}_{2}\)‘ Due to the conservation of linear momentum, \(\vec{p}_{1}^{\prime}+\vec{p}_{2}^{\prime}=0\). It implies that \(\overrightarrow{p_{1}^{\prime}}=-\vec{p}_{2}\) the momentum of the gun is exactly equal, but in the opposite direction to the momentum of the bullet. This is the reason after firing, the gun suddenly moves backwards with the momentum (-\vec{p}_{2}). It is called ‘recoil momentum’. This is an example of conservation of total linear momentum.
[OR]
Question 35(b).
State and prove parallel axis theorem.
Answer:
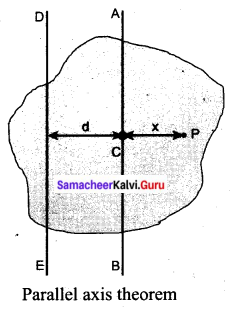
Parallel axis theorem: Parallel axis theorem states that the moment of inertia of a body about any axis is equal to the sum of its. moment of inertia about a parallel axis through its centre of mass and the product of the mass of the body and the square of the perpendicular distance between the two axes.
If IC is the moment of inertia of the body of mass M about an axis passing through the centre of mass, then the moment of inertia I about a parallel axis at a distance d from it is given by the relation,
I = IC + Md2
Let us consider a rigid body as shown in the figure. Its moment of inertia about an axis AB passing through the center of mass is IC. DE is another axis parallel to AB at a perpendicular distance d from AB. The moment of inertia of the body about DE is I. We attempt to get an expression for I in terms of IC. For this, let us consider a point mass m on the body at position x from its centre of mass.
The moment of inertia of the point mass about the axis DE is, m (x + d)2. The moment of inertia I of the whole body about DE is the summation of the above expression.

![]()
Question 36(a).
What is an elastic collision? Derive an expression for final velocities of two bodies which undergo elastic collision in one dimension.
Answer:
Elastic collision: In a collision, the total initial kinetic energy of the bodies (before the collision) is not equal to the total final kinetic energy of the bodies (after collision) then, it is called as inelastic collision, i.e.,
Consider two elastic bodies of masses m1 and m2 moving in a straight line (along positive x-direction) on a frictionless horizontal surface as shown in the figure.
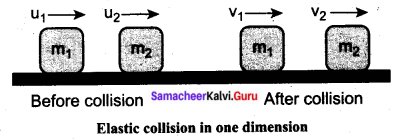
In order to have a collision, we assume that the mass m1 moves faster than mass m2 i.e., u1 > u2. For elastic collision, the total linear momentum and kinetic energies of the two bodies before and after a collision must remain the same.
From the law of conservation of linear momentum,
Total momentum before collision (pi) = Total momentum after collision (pf)

This means that for any elastic head-on collision, the relative speed of the two elastic bodies after the collision has the same magnitude as before collision but in opposite direction. Further note that this result is independent of mass.
Rewriting the above equation for v1 and v2,
v1 = v12 + u2 – u1 ……… (6)
(or) v2 = u1 + v1 – u2 ……. (7)
To find the final velocities v1 and v2:
Substituting equation (7) in equation (2) gives the velocity of m1 as

The equations (10) and (11) show that in a one-dimensional elastic collision when two bodies of equal mass collide after the collision their velocities are exchanged.
Case 2: When bodies have the same mass i.e., m1 = m2 and second body (usually called target) is at rest (u2 = 0),
By substituting m1m2 = 0 and u2 = 0 in equations (8) and equations (9) we get,
from equation (8) ⇒ v1 = 0 ………(12)
from equation (9) ⇒ v2 = u1 ………(13)
Equations (12) and (13) show that when the first body comes to rest the second body moves with the initial velocity of the first body.
Case 3: The first body is very much lighter than the second body \(\left(m_{1}<<m_{2}, \frac{m_{1}}{m_{2}}<<1\right)\) then the ratio \(\frac{m_{1}}{m_{2}} \approx 0\) and also if the target is at rest (u2 = 0)
Dividing numerator and denominator of equation (8) by m2, we get

[OR]
Question 36(b).
How will you determine the velocity of sound using resonance air column apparatus?
Answer:
Resonance air column apparatus: The resonance air column apparatus and first, second and third resonance The resonance air column apparatus is one of the simplest techniques to measure the speed of sound in air at room temperature. It consists of a cylindrical glass tube of one-meter length whose one end A is open and another end B is connected to the water reservoir R through a rubber tube as shown in the figure. This cylindrical glass tube is mounted on a vertical stand with a scale attached to it. The tube is partially filled with water and the water level can be adjusted by raising or lowering the water in the reservoir R. The surface of the water will act as a closed-end and other as the open end. Therefore, it behaves like a closed organ pipe, forming nodes at the surface of water and antinodes at the closed end. When a vibrating tuning fork is brought near the open end of the tube, longitudinal waves are formed inside the air column. These waves move downward as shown in Figure, and reach the surfaces of water and get reflected and produce standing waves.
The length of the air column is varied by changing the water level until a loud sound is produced in the air column. At this particular length, the frequency of waves in the air column resonates with the frequency of the tuning fork (natural frequency of the tuning fork). At resonance, the frequency of sound waves produced is equal to the frequency of the tuning fork. This will occur only when the length of the air column is \(\left(\frac{1}{4}\right)^{t h}\) of the wavelength of the sound waves produced. Let the first resonance occur at length L1, then \(\frac{1}{4} \lambda=\mathrm{L}_{1}\) ……… (1)
But since the antinodes are not exactly formed at the open end, we have to include a correction, called end correction e, by assuming that the antinode is formed at some small distance above the open end. Including this end correction, the first resonance is
\(\frac{1}{4} \lambda=\mathrm{L}_{1}+e\) …….. (2)
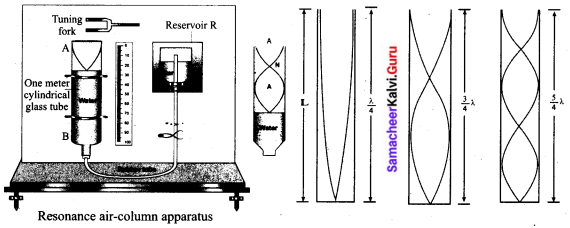
Now the length of the air column is increased to get the second resonance. Let L2 be the length at which the second resonance occurs. Again taking end correction into account, we have
\(\frac{3}{4} \lambda=\mathrm{L}_{2}+e\) ……(3)
In order to avoid end correction, let us take the difference of equation (3) and equation (2)
\(\frac{3}{4} \lambda-\frac{1}{4} \lambda=\left(\mathrm{L}_{2}+e\right)-\left(\mathrm{L}_{1}+e\right) \Rightarrow \frac{1}{2} \lambda=\mathrm{L}_{2}-\mathrm{L}_{1}=\Delta \mathrm{L} \Rightarrow \lambda=2 \Delta \mathrm{L}\)
The speed of the sound in air at room temperature can be computed by using the formula
v = fλ = 2f∆L
Further, to compute the end correction, we use equation (2) and equation (3), we get
\(e=\frac{L_{2}-3 L_{1}}{2}\)
![]()
Question 37(a).
Derive Mayer’s relation for an ideal gas.
Answer:
Mayer’s relation: Consider µ mole of an ideal gas in a container with volume V, pressure P and temperature T.
When the gas is heated at the constant volume the temperature increases by dT. As no work is done by the gas, the heat that flows into the system will increase only the internal energy. Let the change in internal energy be dU.
If Cv is the molar specific heat capacity at constant volume, from the equation.
\(C_{V}=\frac{1}{\mu} \frac{d U}{d T}\) ………. (1)
dU = µCVdT ……. (2)
Suppose the gas is heated at constant pressure so that the temperature increases by dT. If ‘Q’ is the heat supplied in this process and ‘dV’ the change in volume of the gas.
Q = µCPdT …….(3)
If W is the workdone by the gas in this process, then
W = PdV …….. (4)
But from the first law of thermodynamics,
Q = dU + W ……….(5)
Substituting equations (2), (3) and (4) in (5), we get,
µCPdT = µCVdT + PdV
For mole of ideal gas, the equation of state is given by .
PV = µRT ⇒ PdV + VdP = µRdT
Since the pressure is constant, dP = 0
CPdT = CVdT +RdT
CP = CV + R (or) CP – CV = R ……(6)
This relation is called Mayer’s relation It implies that the molar specific heat capacity of an ideal gas at constant pressure is greater than molar specific heat capacity at constant volume. The relation shows that specific heat at constant pressure (sP) is always greater than specific heat at constant volume (sV).
[OR]
Question 37(b).
Explain the horizontal oscillations of a spring.
Answer:
Horizontal oscillations of a spring-mass system: Consider a system containing a block of mass m attached to a massless spring with stiffness constant or force constant or spring constant it placed on a smooth horizontal surface (frictionless surface) as shown in the figure. Let x0 be the equilibrium position or mean position of mass m when it is left undisturbed. Suppose the mass is displaced through a small displacement x towards right from its equilibrium position and then released, it will oscillate back and forth about its mean position x0. Let F be the restoring force (due to stretching of the spring) which is proportional to the amount of displacement of the block. For one dimensional motion, mathematically, we have
F ∝ x
F = -kx ….. (1)
where negative sign implies that the restoring force will always act opposite to the direction of the displacement. This equation is called Hooke’s law. Notice that, the restoring force is linear with the displacement (i.e., the exponent of force and displacement are unity). This is not always true; in case if we apply a very large stretching force, then the amplitude of oscillations becomes very large (which means, force is proportional to displacement containing higher powers of x) and therefore, the oscillation of the system is not linear and hence, it is called non-linear oscillation. We restrict ourselves only to linear oscillations throughout our discussions, which means Hooke’s law is valid (force and displacement have a linear relationship).
From Newton’s second law, we can write the equation for the particle executing simple harmonic motion
\(m \frac{d^{2} x}{d t^{2}}=-k x\) …….. (1)
\(\frac{d^{2} x}{d t^{2}}=-\frac{k}{m} x\) ……. (2)
Comparing the equation with simple harmonic motion equation, we get
\(\omega^{2}=\frac{k}{m}\) ……. (3)
which means the angular frequency or natural frequency of the oscillator is
\(\omega=\sqrt{\frac{k}{m}} \mathrm{rad} \mathrm{s}^{-1}\) ……. (4)
The frequency of the oscillation is
\(f=\frac{\omega}{2 \pi}=\frac{1}{2 \pi} \sqrt{\frac{k}{m}} \text { Hertz }\) …… (5)
and the time period of the oscillation is
\(\mathrm{T}=\frac{1}{f}=2 \pi \sqrt{\frac{m}{k}} \text { seconds }\) ……. (6)
![]()
Question 38.
(a) (i) Write down the equation of a freely falling body under gravity.
(ii) A ball is thrown vertically upwards with the speed of 19.6 ms-1 from the top of a building and reaches the earth in 6s. Find the height of the building.
Answer:
(i) Distance d traveled by an object falling for time ‘t’, u = 0; s = d; a = g
\(\begin{array}{l}
s=u t+\frac{1}{2} a t^{2} \\
d=\frac{1}{2} g t^{2}
\end{array}\)
Time ‘t’ taken for an object to fall distance ‘d’
\(t=\sqrt{\frac{2 d}{g}}\)
Instantaneous velocity vi of a falling object after elapsed time ‘t’
vi = gt
Instantaneous velocity vi of a falling object that has traveled distance ‘d’
\(v_{i}=\sqrt{2 g d}\)
(ii) u = -19.6 ms-1
a = 9.8 ms-2
t = 6 sec
height of the building,
\(\begin{aligned}
s &=u t+\frac{1}{2} a t^{2} \\
&=(-19.6 \times 6)+\frac{1}{2}(9.8)(6)^{2}=-117.6+176.4 \\
s &=58.8 \mathrm{m}
\end{aligned}\)
[OR]
Question 38(b).
(i) Define orbital velocity and establish an expression for it.
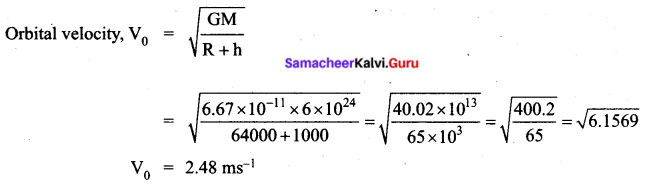
(ii) Calculate the value of orbital velocity for an artificial satellite of earth orbiting at a height of 1000 km (Mass of the earth = 6 × 1024 kg, radius of the earth = 64000 km).
Answer:
(i) Orbital velocity:
Orbital velocity is the velocity given to artificial satellite so that it may start revolving around the earth.
Expression for orbital velocity:
Consider a satellite of mass ‘m’ is revolving around the earth in a circular orbit of radius ‘r’, at a height ‘h’ from the surface of the earth.
Let ‘M’ be the mass of the earth and ‘R’ be the radius of the earth.
Therefore, r = R + h
The centripetal force that is required to revolve the satellite = \(\frac{m v_{0}^{2}}{r}\)
where, V0 is orbital velocity
Orbital velocity is produced by the gravitational force b/w the earth and the satellite = \(\frac{\mathrm{GMm}}{\mathrm{r}^{2}}\)
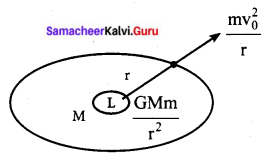
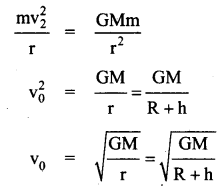
This is the expression for the orbital velocity.
(ii) Mass of the earth M = 6 × 1024 kg
The radius of the earth R = 64000 km
The height of the artificial satellite from the earth (h) = 1000 km
Gravitational constant, (G) = 6.67 × 10-11 Nm-2 kg-2