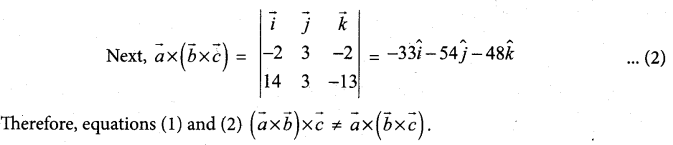Students can Download Tamil Nadu 12th Maths Model Question Paper 4 English Medium Pdf, Tamil Nadu 12th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 12th Maths Model Question Paper 4 English Medium
Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- questions of Part I, II. III and IV are to be attempted separately
- Question numbers 1 to 20 in Part I are objective type questions of one -mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
- Question numbers 21 to 30 in Part II are two-marks questions. These are to be answered in about one or two sentences.
- Question numbers 31 to 40 in Parr III are three-marks questions, These are to be answered in about three to five short sentences.
- Question numbers 41 to 47 in Part IV are five-marks questions. These are to be answered) in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Maximum Marks: 90
Part – I
I. Choose the correct answer. Answer all the questions. [20 × 1 = 20]
Question 1.
The rank of the matrix \(\left[\begin{array}{rrrr}
1 & 2 & 3 & 4 \\
2 & 4 & 6 & 8 \\
-1 & -2 & -3 & -4
\end{array}\right]\) is ………….
(a) 1
(b) 2
(c) 4
(d) 3
Answer:
(a) 1
Question 2.
If \(\left|z-\frac{3}{z}\right|\) , then the least value of | z | is
(a) 1
(b) 2
(c) 3
(d) 5
Answer:
(a) 1
![]()
Question 3.
The product of all four values of ‘\(\left(\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}\right)^{\frac{3}{4}}\) is ………….
(a) -2
(b) -1
(c) 1
(d) 2
Answer:
(c) 1
Question 4.
The value of cos-1(-1) + tan-1(∞) + sin-1 1 = ………….
(a) 3π/2
(b) -π
(c) 2π
(d) 3π
Answer:
(c) 2π
Question 5.
The value of sin -1(1) + sin-1(0) is
(a) π/2
(b) 0
(c) 1
(d) π
Answer:
(a) π/2
Question 6.
The length of the diameter of the circle which touches the x -axis at the point (1,0) and passes through the point (2, 3)
(a) 6/5
(b) 5/3
(c) 10/3
(d) 3/5
Answer:
(c) 10/3
Question 7.
Area of the greatest rectangle inscribed in the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) is ………….
(a) 2ab
(b) ab
(c) \(\sqrt{a b}\)
(d) a/b
Answer:
(a) 2ab
![]()
Question 8.
The angle between two vectors \(\vec{a}\) and \(\vec{b}\) if \(|\vec{a} \times \vec{b}|=\vec{a} \cdot \vec{b}\) is ………….
(a) π/4
(b) π/3
(c) π/6
(d) π/2
Answer:
(a) π/4
Question 9.
The distance between the planes x + 2y + 3z + 7 = 0 and 2x + 4y + 6z + 7 = 0 is ………….

Answer:
(a) \(\frac{\sqrt{7}}{2 \sqrt{2}}\)
Question 10.
The tangent to the curve y2 – xy + 9 = 0 is vertical when
(a) y = 0
(b) y = ± √3
(c) y = 1/2
(d) y = ± 3
Question 11.
The curve y2 = (x – a) (x – b)2, a, b> 0 and a > b does not exist for
(a) x ≥ a
(b) x = b
(c) b < x < a
(d) x = a
Question 12.
The percentage error of fifth root of 31 is approximately how many times the percentage error in 31 ?
(a) 1/31
(b) 1/5
(c) 5
(d) 31
Answer:
(b) 1/5
![]()
Question 13.
The differential of y if y =\(\frac{x-2}{2 x+3}\) is ………….
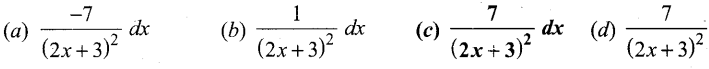
Answer:
(c) \(\frac{7}{(2 x+3)^{2}} d x\)
Question 14.
If \(\int_{0}^{a} \frac{1}{4+x^{2}} d x=\frac{\pi}{8}\) then a is ………….
(a) 4
(b) 1
(c) 3
(d) 2
Answer:
(d) 2
Question 15.
If n is off then \(\int_{0}^{\frac{\pi}{2}} \cos ^{n} x d x\) is

Answer:
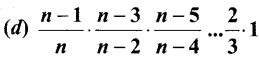
Question 16.
The solution of \(\frac{d y}{d x}+p(x) y=0\) is
(a) y = ce∫pdx
(b) y = ce-∫pdx
(c) x = ce-∫pdx
(d) x = ce∫pdx
Answer:
(b) y = ce-∫pdx
Question 17.
The order and degree of the differential equation are \(\frac{d^{2} y}{d x^{2}}-y+\left(\frac{d y}{d x}+\frac{d^{3} y}{d x^{3}}\right)^{\frac{3}{2}}=0\) ………….
(a) 2, 3
(b) 3,3
(c) 3, 2
(d) 2, 2
Answer:
(b) 3,3
Question 18.
The random variable X has the probability density function \(f(x)=\left\{\begin{array}{cc}
a x+b, & 0<x<1 \\
0, & \text { otherwise }
\end{array}\right.\) and E(X) = —, then a and b are respectively ………….
(a) 1 and 1/2
(b) 1/2 and 1
(c) 2 and 1
(d) 1 and 2
Answer:
(a) 1 and 1/2
![]()
Question 19.
If the function f(x) = 1/12 for a < x < b represents a probability density function of a continuous random variable X, then which of the following cannot be the value of a and b?
(a) 0 and 12
(b) 5 and 17
(c) 7 and 19
(d) 16 and 24
Answer:
(d) 16 and 24
Question 20.
Which one of the following is not true?
(a) Negation of a negation of a statement is the statement itself.
(b) If the last column of the truth table contains only T then it is a tautology.
(c) If the last column of its truth table contains only F then it is a contradiction
(d) If p and q are any two statements then p ↔ q is a tautology.
Answer:
(d) If p and q are any two statements then p ↔ q is a tautology.
Part – II
II. Answer any seven questions. Question No.30 is compulsory [7 x 2 = 14]
Question 21.
If adj [A] = \(\left[\begin{array}{ccc}
0 & -2 & 0 \\
6 & 2 & -6 \\
-3 & 0 & 6
\end{array}\right]\) then find A-1
Answer:
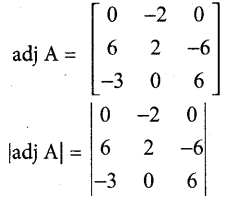

Question 22.
Obtain the condition that the roots of x3 + px2 + qx + r = 0 are in A.P.
Answer:
Let the roots be in A.R Then, we can assume them in the form α – d, α, α + d. Applying the Vietas formula (α – d) + α + (α + d) = -y = \(-\frac{p}{1}\) => 3α = -p => α = \(-\frac{p}{3}\)
But, we note that a is a root of the given equation. Therefore, we get
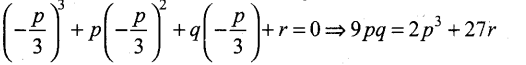
Question 23.
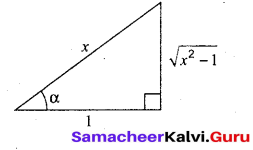
Show that \(\cot ^{-1}\left(\frac{1}{\sqrt{x^{2}-1}}\right)=\sec ^{-1} x\) |x| > 1
Answer:
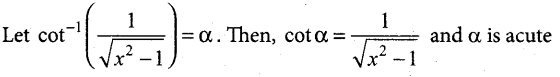
We construct a right triangle with the given data.
From the triangle, sec α = \(\frac{x}{1}\) = x. Thus, α = sec-1 x.
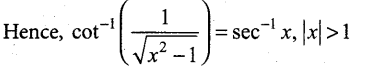
Question 24.
Evaluate \(\lim _{x \rightarrow 1} x^{\frac{1}{x-1}}\)
Answer:

Question 25.
The radius of a circular disc is given as 24 cm with a maximum error in measurement of 0.02 cm. (i) Use differentials to estimate the maximum error in the calculated area of the disc, (ii) Compute the relative error.
Answer:
r = 24 cm, dr = 0;02 cm
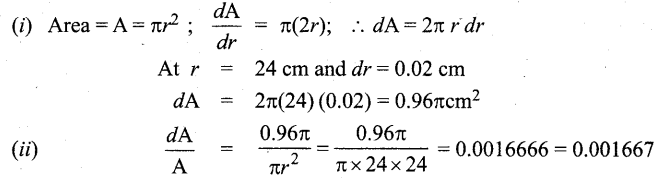
Question 26.
Evaluate \(\int_{-\log 2}^{\log 2} e^{-|x|} d x\)
Answer:
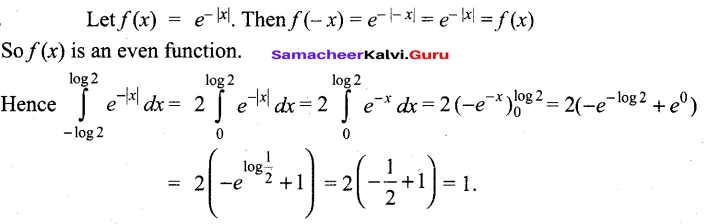
![]()
Question 27.
Show that the following expressions is a solution of the corresponding given differential equation.
y = aex + be-x ; y” – y = 0
Answer:
y = aex + be-x …(1) Differential equation: y”- y = 0
Differentiate with respect to ‘x’
y’ = aex – be-x
Again differentiate with respect to ‘x’
y”= aex + be-x
y” = y ⇒ y” – y = 0
∴ (1) is the solution of the given differential equation.
Question 28.
Suppose X is the number of tails occurred when three fair coins are tossed once simultaneously. Find the values of the random variable X and number of points in its inverse images.
Answer:
Let X is the random variable denotes the number of tails when three coins are tossed simultaneously.
Sample space S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
∴ ‘X’ takes the values 0, 1, 2, 3
i.e., X (HHH) = 0 ; X (HHT, HTH, THH) = 1 ; X (HTT, THT, TTH) = 2 ; X (TTT) = 3

Question 29.
Verify the (i) closure property (it) commutative property (iii) associative property ‘ (iv) existence of identity and (v) existence of inverse for the arithmetic operation + on Zo = the set of all odd integers.
Answer:
Consider the set Z0 of all odd integers Z0 = {2k + 1 : k ∈ Z} = 5,—3,-1, 1 ,3 ,5, …}. + is not a binary operation on Z0 because when x = 2m + 1, y = 2n + 1,
x + y = 2(m + n) + 2 is even for all m and n. For instance, consider the two odd numbers 3,7 ∈ Z0. Their sum 3 + 7 = 10 is an even number. In general, if x, y ∈ Z 0, then (x + y)∉ Z 0
Other properties need not be checked as it is not a binary operation.
Question 30.
Simplify i1948 – i1869
Answer:
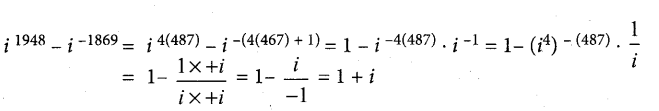
Part – III
III. Answer any seven questions. Question No. 40 is compulsory. [7 x 3 = 21]
Question 31.
Find the inverse of the matrix \(\left[\begin{array}{rrr}
2 & -1 & 3 \\
-5 & 3 & 1 \\
-3 & 2 & 3
\end{array}\right]\)
Answer:

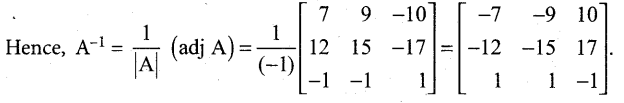
Question 32.
Find the value of \(\left(\frac{1+\sin \frac{\pi}{10}+i \cos \frac{\pi}{10}}{1+\sin \frac{\pi}{10}-i \cos \frac{\pi}{10}}\right)^{10}\)
Answer:
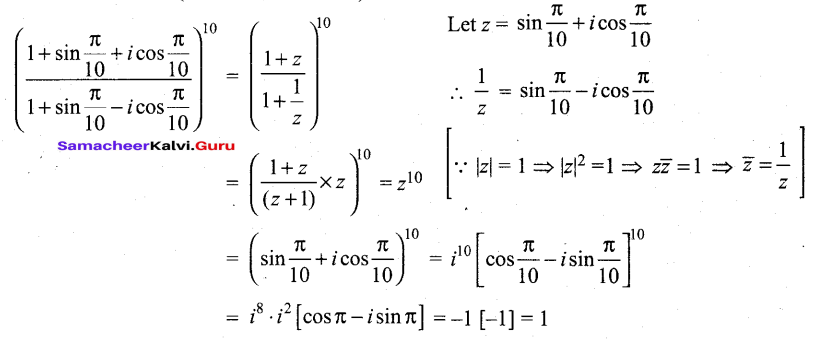
Question 33.
Foci (0, ± 4) and end points of major axis are(0, ± 5). Find the equation of the ellipse.
Answer:
From the diagram we see that major axis is along y-axis.
Also a = 5 and ae = 4
⇒ 5e = 4 ⇒e = 4/5
Now a = 5 ⇒ a2 = 25
ae = 4 ⇒ ae2 =16
So b2= a2(1 – e2) = a2– a2e2 = 25 – 16 = 9
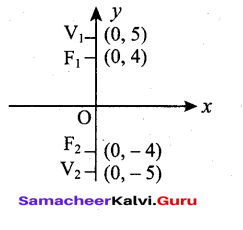
![]()
Question 34.
Show that the two lines \(\vec{r}=(\vec{i}-\vec{j})+t(2 \vec{i}+\vec{k}) \text { and } \vec{r}=(2 \vec{i}-\vec{j})+s(\vec{i}+\vec{j}-\vec{k})\) lines and find the distance between them.
Answer:
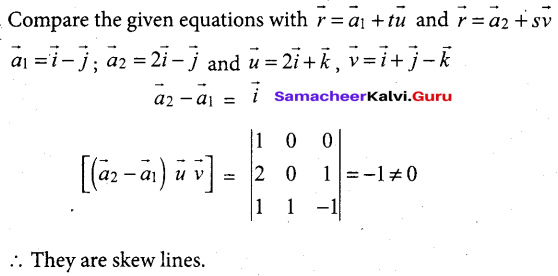
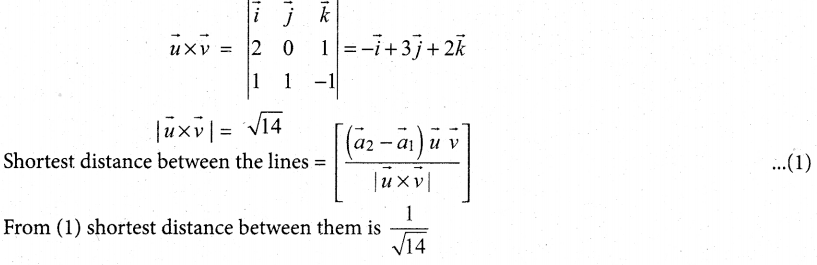
Question 35.
Find the local maximum and minimum of the function x2 y2 on the line x+y = 10.
Answer:
Let the given function be written as f(x) = x2(10 – x)2. Now,
f(x) = x2 (100 – 20x + x2) = x4 – 20x3 + 100x2
Therefore, f’ (x) = 4x3 – 60x2 + 200x = 4x (x2 – 15x + 50)
f'(x) = 4x(x2 – 15x + 50) = 0 ⇒ x = 0, 5, 10
and f ” (x) = 12x2 – 120x + 200
The stationary points of /(x) are x = 0, 5, 10 at these points the values of f” (x) are respectively 200, -100 and 200. At x = 0, it has local minimum and its value is f(0) = 0. At x = 5, it has local maximum and its value is f(5) = 625. At x =10, it has local minimum and its value is f(10) = 0.
Question 36.
Let U(x, y, z) = x2 – xy + 3sin z, x, y, z ∈ R. Find the linear approximation for U at (2,-1,0).
Answer:
Linear approximation is given by
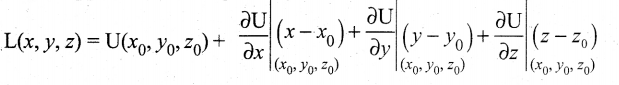
Now Ux = 2x – y, Uy = – x and Uz = 3cos z.
Here (x0,y0,z0) = (2, -1,0), hence Ux(2, -1,0) = 5, Uy(2, -1,0) = -2 and Uz (2, -1,0) = 3.
Thus L(x, y, z) = 6 + 5(x – 2) – 2(y + 1) + 3(z – 0) = 5x – 2y + 3z – 6 is the required linear approximation for U at (2,-1,0).
Question 37.
Find the volume of a sphere of radius a.
Answer:
By revolving the upper semicircular region enclosed between the circle x2 + y2 = a2 and the x-axis, we get a sphere of radius a.
The boundaries of the region are y = \(\sqrt{a^{2}-x^{2}}\) x-axis x = -a and x= a Hence, the volume of the sphere is given by

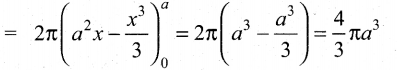
Question 38.
Solve the following differential equations: ydx + (1 + x2) tan-1 x dy = 0
Answer:
ydx + (1 + x2) tan-1 x dy =0
(1 + x2) tan-1 x dy= -y dx
Separating the variables

log y = – log (tan-1x) + log c
log y + log (tan-1 x) = log c
log (y tan-1 x) = log c
y tan-1 x = c
![]()
Question 39.
Prove that \(\boldsymbol{q} \rightarrow \boldsymbol{p} \equiv \neg \boldsymbol{p} \rightarrow \neg \boldsymbol{q}\)
Answer:
Truth table for q → p
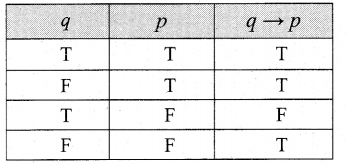
Truth table for \(\neg p \rightarrow \neg q\)
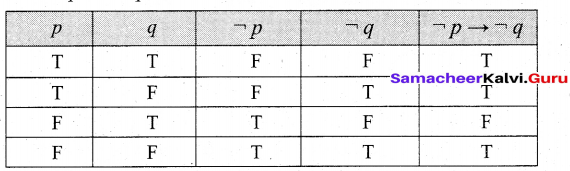
The entries in the column corresponding to q → p and \(\neg p \rightarrow \neg q\) are identical and hence they are equivalent.
Question 40.
If on an average 1 ship out of 10 do not arrive safely to ports. Find the mean and the standard deviation of the ships returning safely out of a total of 500 ships.
Answer:
Probability of a ship arriving safely

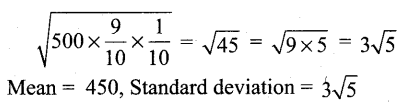
Part – IV
IV. Answer all the questions. [7 x 5 = 35]
Question 41.
(a) If F(α) = \(\left[\begin{array}{ccc}
\cos \alpha & 0 & \sin \alpha \\
0 & 1 & 0 \\
-\sin \alpha & 0 & \cos \alpha
\end{array}\right]\) show that F[(α)]-1 = F(-α)
Answer:
Let A = F(α)
So F[(α)]-1 = F(-α)

Expanding the determinant – along R2 We get
-0() + 1 [cos2α + sin2α] – 0() = 1 ≠ 0
So A-1 exists

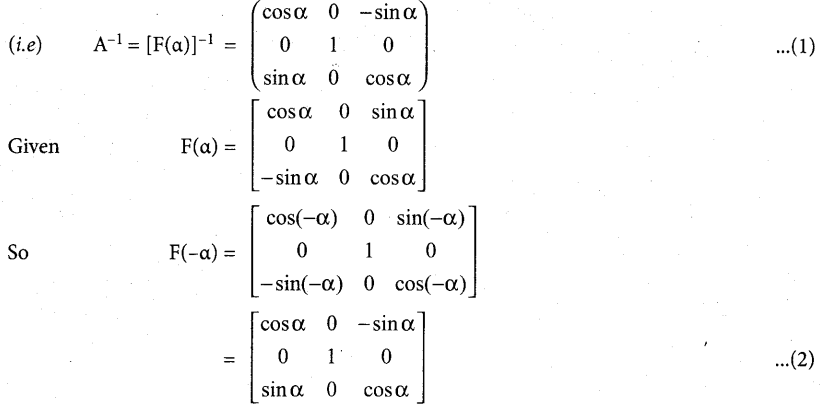

[OR]
(b) If ω ≠ 1 is a cube root of unity, show that the roots of the equation (z – 1)3 + 8 = 0 are -1,1- 2ω , 1- 2ω2
Answer:
(z- 1)3 + 8 = 0 ⇒ (z – 1)3 = -8

Question 42.
(a) Solve: \((\sqrt{3}+\sqrt{2})^{x}+(\sqrt{3}-\sqrt{2})^{x}=10\)
Answer:


[OR]
(b) If a1 a2, a3,… an is an arithmetic progression with common difference d. Prove that
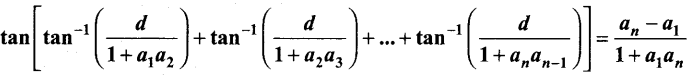
Answer:

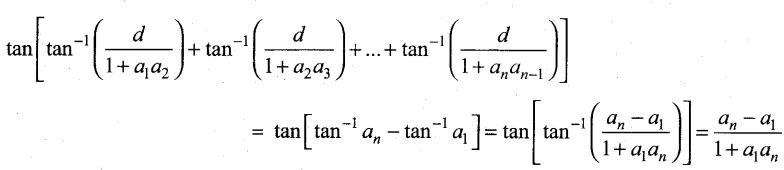
![]()
Question 43.
(a) Show that the linex-y + 4 = 0isa tangent to the ellipse x2 + 3y2 = 12. Also find the coordinates of the point of contact.
Answer:
The given ellipse is x2 + 3y2 =12
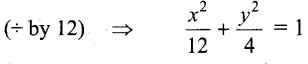
(ie.,) Here a2 = 12 and b2 = 4
The given line is x – y + 4 = 0
(ie.,) y = x + 4
Comparing this line with y = mx + c
We get m = 1 and c = 4
The condition for the line y = mx + c
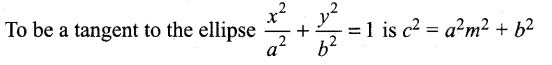
LHS = c2 = 42 = 16
RHS: a2m2 + b2 = 12(1)2 + 4=16
LHS = RHS ⇒ The given line is a tangent to the ellipse. Also the point of contact is
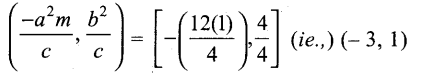
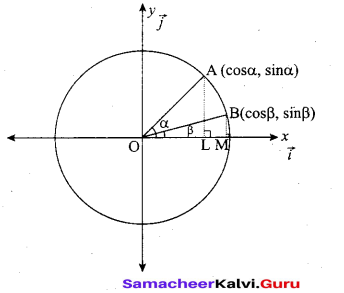
(b) Using vector method, prove that cos(α – β) = cos α cos β + sin α sin β
Answer:
Take two points A and B on the unit circle with centre
as origin ‘O’. so \(|\overrightarrow{\mathrm{OA}}|=|\overrightarrow{\mathrm{OB}}|=1\)
\(\mathrm{AO} x=\alpha ; \quad \mathrm{BO} x=\beta \Rightarrow \mathrm{LAOB}=\alpha-\beta\)
Let \(\vec{i}\) and \(\vec{j}\) be the unit vectors along the x, y respectively.
The co-ordinates of A and B be (cos α, sin α) and (cos β, sin β) respectively.

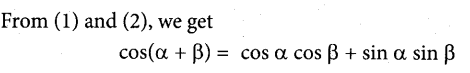
Question 44.
(a) A farmer plans to fence a rectangular pasture adjacent to a river. The pasture must contain 1,80,000 sq. mtrs in order to provide enough grass for herds. No fencing is needed along the river. What is the length of the minimum needed fencing material?
Answer:
Given Area = 180000 sqm
Let length be x and breadth be y
Now xy = 180000
⇒ y = \( \frac{180000}{x}\)
Now perimeter = 2x + y(∵one side is along ther river)

at x = 300 m, p is positive ⇒ x = 300 is a minimum point
180000
when x = 300 m, y = \( \frac{180000}{300}\) = 600 m
So minimum perimeter = 2x + y
= 2(300) + 600 = 1200 m
[OR]
(b) If u = log (tan x + tan y + tan z), prove that \(\Sigma \sin 2 x \frac{\partial u}{\partial x}=2\)
Answer:
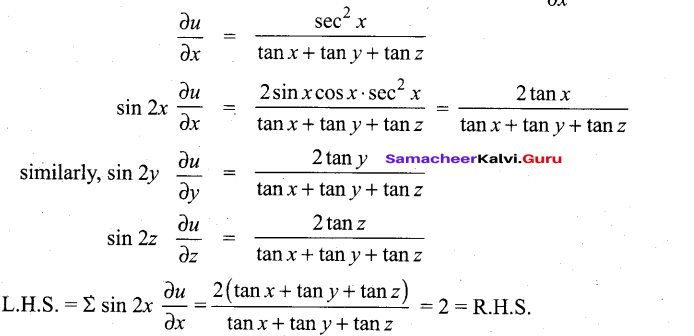
Question 45.
(a) Evaluate as the limit of sums: \(\int_{1}^{2}\left(x^{2}-1\right) d x\)
Answer:
Let f(x) = x2 – 1 for 1≤ x ≤ 2
We divide the interval [1,2] into n equal sub-intervals each of length h. We have a = 1, b = 2
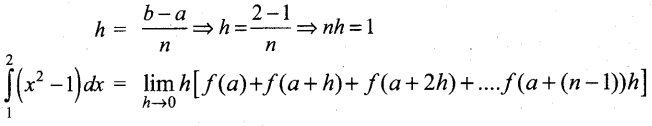
Here,f(a) = f(1) = (1)2 – 1 = 0
f(a + h) = f(1 + h) = (1 + h)2 – 1 = 1 + h2 + 2h – 1 = h2 + 2h
f(a + 2h) = f(1 + 2h) = (1 +2h)2 = 1 + 4h2 + 4h – 1 = 4h2 + 4h
f[a + (n -1) h] = f[1 + (n -1) A] = [1 + (n -1) h]2 – 1
= 1 + (n – 1)2 h2 + 2(n – 1) h – 1 = (n – 1)2 h2 + 2(n – 1) h2

(b) Solve \(\frac{d y}{d x}=\frac{x-y+5}{2(x-y)+7}\)
Answer:


Integrating both sides, we get
2z + 3 log |z + 2| =x + c
That is, 2(x – y) + 3 log |x – y + 2| = x + c
![]()
Question 46.
(a) For the random variable X with the given probability mass function as below, find the mean and variance.
\(f(x)=\left\{\begin{array}{ll}
2(x-1), & 1<x<<2 \\
0 & , \quad \text { otherwise }
\end{array}\right.\)
Answer:

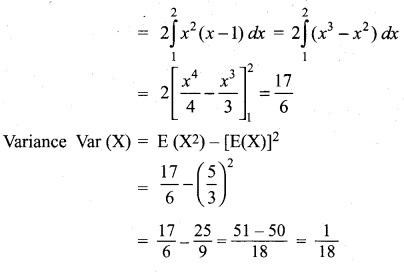
(b) Show that the set { [1], [3], [4], [5], [9]} under multiplication modulo 11 satisfies closure, associative, identity and inverse properties.
Answer:
G = {[1], [3], [4], [5], [9]}
* is defined by multiplication modulo 11.
To prove G is an abelian group with respect to *
Since we are given a finite number of elements i.e., since the given set is finite, we can frame the multiplication table called Cayley’s table.
The Cayley’s table is as follows:
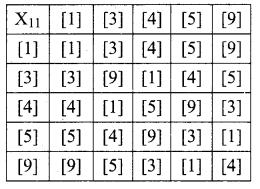
G1: The elements in the above table are [1], [3], [4], [5] and [9] which are elements of G.
.’. closure axiom is verified.
G2 : Consider [3], [4], [5] which are elements of G.
{[3]*[4]}*[5] = [1]*[5] = [5] ……….(1)
[3] *{[4]*[5]} = [3]*[9] = [5] ……….(2)
(1) = (2) ⇒ (a * b) * c = a * (b * c) i.e., associative axiom is verified.
G3 : The first row elements are the same as that of the given elements in the same order.
i.e., from the table, the identity element is [1] ∈ G. So identity axiom is verified.
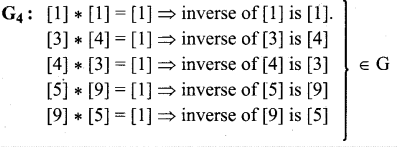
inverse axiom is verified.
G5 : From the table * is commutative i.e., the entries equidistant from the leading diagonal on either sides are equal ⇒ a * b = b * a
![]()
Question 47.
(a) For the ellipse 4x2 + y2 + 24x – 2y + 21 = 0, find the centre, vertices, and the foci. Also prove that the length of latus rectum is 2.
Answer:
Rearranging the terms, the equation of ellipse is ,
4x2 + 24x + y2 – 2y + 21 = 0
That is, 4(x2 + 6x + 9 – 9) + (y2 – 2y + 1 – 1) + 21 =0
4 (x +3)2 – 36 + (y-1)2 – 1 + 21 = 0
4 (0+ 3)2 + (y – 1)2 = 16
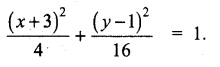
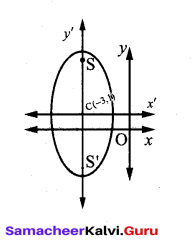
Centre is (-3,1) a = 4, b = 2, and the major axis is parallel to y -axis
c2 = 16 – 4 = 12
c = ± 2 √3
Therefore, the foci are (-3, 2√ +1) and (-3, -2√3 + 1).
Vertices are (1,± 4 +1). That is the vertices are (1, 5) and (1, -3), and
The length of Latus rectum = \(\frac{2 b^{2}}{a}\) = 2 units
[OR]
(b) If \(\vec{a}=-2 \hat{i}+3 \hat{j}-2 \hat{k}, \vec{b}=3 \hat{i}-\hat{j}+3 \hat{k}, \vec{c}=2 \hat{i}-5 \hat{j}+\hat{k}\) find \((\vec{a} \times \vec{b}) \times \vec{c}\) and \(\vec{a} \times(\vec{b} \times \vec{c})\)
State whether they are equal.
Answer: