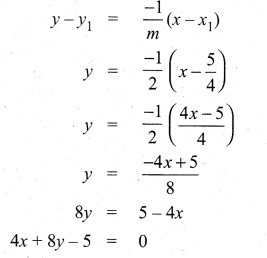Tamil Nadu 12th Maths Model Question Paper 5 English Medium

Students can Download Tamil Nadu 12th Maths Model Question Paper 5 English Medium Pdf, Tamil Nadu 12th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 12th Maths Model Question Paper 5 English Medium

Instructions:

1. 1.  The question paper comprises of four parts.
   2.  You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
   3. questions of Part I, II. III and IV are to be attempted separately
   4. Question numbers 1 to 20 in Part I are objective type questions of one -mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
   5. Question numbers 21 to 30 in Part II are two-marks questions. These are to be answered in about one or two sentences.
   6. Question numbers 31 to 40 in Parr III are three-marks questions, These are to be answered in about three to five short sentences.
   7. Question numbers 41 to 47 in Part IV are five-marks questions. These are to be answered) in detail. Draw diagrams wherever necessary.

Time: 3 Hours
Maximum Marks: 90

Part – I

I. Choose the correct answer. Answer all the questions.  [20 × 1 = 20]

Question 1.
If A = \(\left[\begin{array}{ll}
3 & 5 \\
1 & 2
\end{array}\right]\) B = adj A and C = 3A, then |Adjb| / |C| =  ……………….
(a) 1/3
(b) 1/9
(c) 1/4
(d) 1
Answer:
(b) 1/9

Question 2.
If the inverse of the matrix \(\left[\begin{array}{cc}
1 & 2 \\
3 & -5
\end{array}\right]\) is \(\frac{1}{11}\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\) , then the ascending order of a, b, c, d, is
(a) a, b, c, d
(b) d, b, c, a
(c) c, a, b, d
(d) b, a, c, d
Answer:
(b) d, b, c, a

Question 3.
The least value of n satisfying \(\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^{n}\) = 1 is
(a) 30
(b) 24
(c) 12
(d) 18
Answer:
(c) 12

Question 4.
The principal argument of \(\frac{3}{-1+i}\) is

Answer:
(c) \(\frac{-3 \pi}{4}\)

Question 5.
The polynomial equation x³ + 2x + 3 = 0 has
(a) one negative and two imaginary
(b) one positive and two imaginary roots
(c) three real roots
(d) no solution
Answer:
(a) one negative and two imaginary

Question 6.
The domain of the function defined by \(f(x)=\sin ^{-1}(\sqrt{x-1})\) is
(a) [1, 2]
(b) [-1,1]
(c) [0, 1]
(d) [-1, 0]
Answer:
(a) [1, 2]

Question 7.
If x+y = A:isa normal to the parabola y² = 12x, then the value of k is
(a) 3
(b) -1
(c) 1
(d) 9
Answer:
(d) 9

Question 8.
The circle passing through (1, -2) and touching the x-axis (3,0), again passing through the point is
(a)(-5,2)
(b) (2,-5)
(c) (5, -2)
(d) (-2,5)
Answer:
(c) (5, -2)

Question 9.
The volume of the parallelepiped with its edges represented by the vectors \(\hat{i}+\hat{j}, \hat{i}+2 \hat{j}, \hat{i}+\hat{j}+\pi \hat{k}\) is
(a) \(\frac{\pi}{2}\)
(b) \(\frac{\pi}{3}\)
(c) π
(d) \(\frac{\pi}{4}\)
Answer:

Question 10.
If the line \(\frac{x-2}{3}=\frac{y-1}{-5}=\frac{z+2}{2}\) lies in the plane x + 3y – αz + β = 0 then (α, β) is ………………
(a) (-5, 5)
(b) (-6, 7)
(c) (5, -5)
(d) (6, -7)
Answer:
(b) (-6, 7)

Question 11.
The function sin⁴ + cos⁴x is increasing in the interval

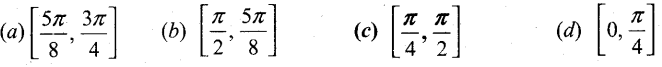
Answer:
(c) \(\left[\frac{\pi}{4}, \frac{\pi}{2}\right]\)

Question 12.
The curve y = ax⁴ + bx² with ab> 0
(a) has no horizontal tangent
(b) is concave up
(c) is concave down
(d) has no points of inflection
Answer:
(d) has no points of inflection

Question 13.
If u = (x-y)², then \(\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}\) is …………….
(a) 1
(b) -1
(c) 0
(d) 2
Answer:
(c) 0

Question 14.
The value of \(\int_{0}^{\pi} \frac{d x}{1+5 \cos x}\) is …………….
Answer:
(a) \(\frac{\pi}{2}\)
(b) π
(c) \(3\frac{\pi}{2}\)
(d) 2π
Answer:
(a) \(\frac{\pi}{2}\)

Question 15.
The volume of solid of revolution of the region bounded by y² = x(a – x) about x – axis is …….

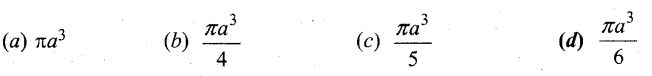
Answer:
(d) \(\frac{\pi a^{3}}{6}\)

Question 16.
If m, n are the order and degree of the differential equation \(\left[\frac{d^{4} y}{d x^{4}}+\frac{d^{2} y}{d x^{2}}\right]^{\frac{1}{2}}=a \frac{d^{2} y}{d x^{2}}\) respectively, then the value of 4m – n is
(a) 15
(b) 12
(c) 14
(d) 13
Answer:
(a) 15

Question 17.
The solution of differential equation \(\frac{d y}{d x}=\frac{y}{x}+\frac{\varphi\left(\frac{y}{x}\right)}{\varphi^{\prime}\left(\frac{y}{x}\right)}\) is

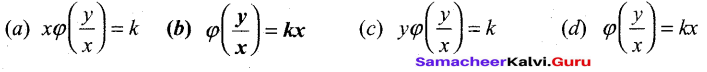
Answer:
(b) \(\varphi\left(\frac{y}{x}\right)=k x\)

Question 18.
A random variable X has the following distribution.

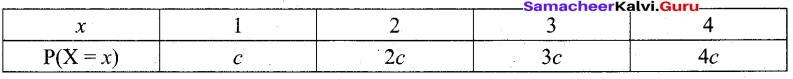
then the value of c is
(a) 0.1
(b) 0.2
(c) 0.3
(d) 0.4
Answer:
(a) 0.1

Question 19.
If P(X = 0) = 1 – P {X = 1} and E[X] = 3 Var (X), then P{X = 0} is
(a) \(\frac{2}{3}\)
(b) \(\frac{2}{5}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{1}{5}\)
Answer:
(c) \(\frac{1}{3}\)

Question 20.
Which one is the contrapositive of the statement (p v q) → r?

Answer:
(a) \(\neg r \rightarrow(\neg p \wedge \neg q)\)

Part – II

II. Answer any seven questions. Question No. 30 is compulsory. [7 x 2 = 14]

Question 21.
Solve the following system of linear equations by Cramer’s rule: 2x – y = 3,x + 2y = -1.
Answer:
2x – y = 3, x + 2y 2 -1 = -1

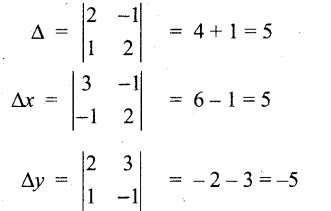
Question 22.
If z₁ z₂ and z₃ are complex numbers such that |z₁| = |z₂| = |z₃| = |z₁+ z₂ + z₃| = 1 find the value of \(\left|\frac{1}{z_{1}}+\frac{1}{z_{2}}+\frac{1}{z_{3}}\right|\)
Answer:

Question 23.
Find the value of \(\sin \left(\frac{\pi}{3}+\cos ^{-1}\left(\frac{-1}{2}\right)\right)\)
Answer:

Question 24.
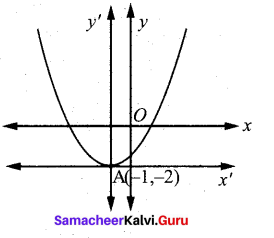
Find the equation of the parabola with vertex (-1,-2), axis parallel to x-axis and passing through (3, 6).
Answer:
Since axis is parallel to y-axis the required equation of the parabola is (x + 1)² = 4a (y + 2)
Since this passes through (3,6)
(3 + 1)² = 4a (6 + 2)
a = 1/2
Then the equation of parabola is (x + 1)² = 2 (y + 2) which on simplifying yields,
x² + 2x – 2y – 3 = 0.

Question 25.
If â, b̂, ĉ are three unit vectors such that b̂ and ĉ are non-parallel and â, x (b̂ x ĉ) = \(\frac{1}{2} \hat{b}\), find the angle between â and ĉ.
Answer:

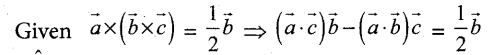
Since b and c are non collinear vectors. So, equating corresponding coefficients on both sides.

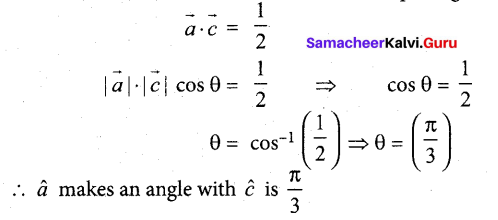
Question 26.
If the mass m(x) (in kilograms) of a thin rod of length x (in meters) is given by, m(x) = \(m(x)=\sqrt{3 x}\) then what is the rate of change of mass with respect to the length when it is x = 27 metres?
Answer:

Question 27.
Evaluate \(\int_{0}^{\infty} e^{-a x} x^{n} d x\) where a > 0.
Answer:
Making the substitution t = ax, we get dt = adx and x = 0 ⇒ t = 0 and x = ∞ ⇒ t = ∞. Hence, we get

Question 28.
Show that y = ax + b/x, x ≠ 0 is a solution of the differential equation x²y” + xy’ – y = 0.
Answer:
Given solution : y = ax + \(\frac{b}{x}\)  …………..(1)
y = ax + \(\frac{b}{x}\)
xy = ax²+b
Differentiate with respect to ‘x’
xy’ + y.1 = a(2x) = 2ax …(2)
Differentiate again with respect to ‘x’
xy” + y’ . 1 + y’ = 2a ⇒ xy” + 2y’ = 2a …(3)
Substitute (3) in (2)
xy’ + y = (xy” + 2y’) x
xy’+ y = x²y” + 2xy’ ⇒ x²y” + xy’- y = 0
Hence proved.

Question 29.
Find the mean of a random variable X, whose probability density function is
\(f(x)=\left\{\begin{array}{l}
\lambda e^{-\lambda x} \text { for } x \geq 0 \\
0 \text { otherwise }
\end{array}\right.\)
Answer:

Question 30.
Let * be a binary operation on set Q of rational numbers defined as a * b = \(\frac{a b}{8}\) Write the identity for * if any.
Answer:
Let S = {Q}
a * b = \(\frac{a b}{8}\)
∀ a∈S, e∈S such that
a * e = a
\(\frac{a e}{8}=a\) ⇒ ae = 8a
e = 8 ∈ S .
Identity element exist.

Part – III

III. Answer any seven questions. Question No. 40 is compulsory. [7 x 3 = 21]

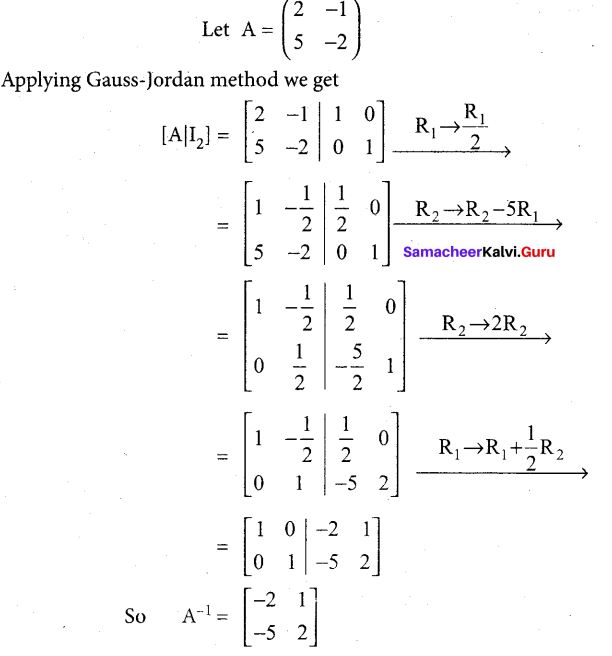
Question 31.
Find the inverse of \(\left[\begin{array}{cc}
2 & -1 \\
5 & -2
\end{array}\right]\) by Gauss-Jordan method.
Answer:

Question 32.
If w ≠ 1 is a cube root of unity, show that the roots of the equation (z – 1)³ + 8 = 0 are -1,1- 2w, 1- 2 w²
Answer:

Question 33.
Find all real numbers satisfying 4^x – 3(2^x+2) + 2⁵ = 0
Answer:
4^x – 3 (2^x+2) + 25 = 0
⇒ (2²)^x – 3 (2^x ,2²) + 25 = 0
(2²)^x – 12 .2^x + 32 = 0
Let y = 2^x
y² – 12y + 32 = 0
(y – 4) (y – 8) = 0 .
y = 4,8
Case (i) 2^x = 4
2^x= (2)² ⇒ x = 2
Case (ii) 2^x = 8
2^x = (2)³ ⇒x = 3
∴ The roots are 2, 3

Question 34.
Find the centre, foci, and eccentricity of the hyperbola 12x² – 4y² – 24x + 32y – 127 = 0.
Answer:
12x² – 4y²– 24x + 32y – 127 = 0
12[x² – 2x] – 4[y² – 8y] = 127
12[(x – 1)² – 1] – 4[(y – 4)² – 16] = 127
12(x – 1)²– 4(y – 4)² = 127 +12 – 64
12(x- 1)² – 4(y-4)² = 75

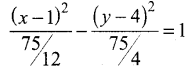
Let X = x – 1; Y = y – 4

(i) Centre : c[0,0]
X = o
x – 1 = 0
x = 1

Y = o
y – 4 = 0
y = 4

Centre (1,4)

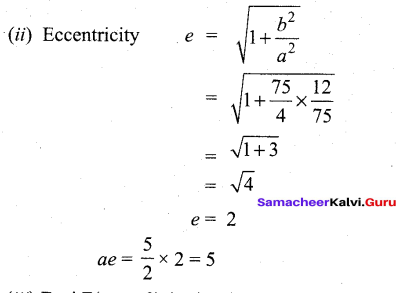
(iii) Foci F(± ae, 0) (i.e.,) F (± 5, 0)
X = 5
x- 1 = 5
x = 6
X = -5
x – 1 = -5
x = -4
Y = 0
y – 4 = 0
y = 4
Foci (6, 4) and (-4, 4)

Question 35.
Find the image of the point whose position vector is \(\hat{i}+2 \hat{j}+3 \hat{k}\) in the plane \(\vec{r} \cdot(\hat{i}+2 \hat{j}+4 \hat{k})=38\)
Answer:

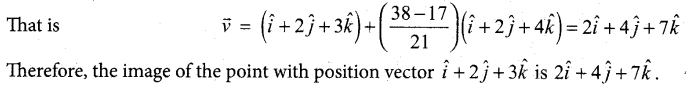
Question 36.
Evaluate:  \(\lim _{x \rightarrow 0^{+}} x \log x\)
Answer:
This is an indeterminate of the form (0 x ∞). To evaluate this limit, we first simplify and bring it to the form (∞/∞) and apply 1’Hopital Rule

Question 37.
Find a linear approximation for the function given below at the indicate points f(x) = x³ -5x + 12, x₀ = 2.
Answer:
f(x) = x³ – 5x + 12 .
f'(x) = 3x² – 5
f(x₀) = f(2) = (2)³– 5(2) + 12 = 8 – 10 + 12 = 10
f'(x₀) = f'(2) = 3(2)² – 5 = 12 – 5 = 7
The required linear approximation L(x) = f(x₀) + f’ (x₀) (x – x₀)
= 10 + 7 (x – 2)
= 10 + 7x – 14
= 7x – 4

Question 38.
By using the properties of definite integrals, evaluate \(\int_{0}^{3}|x-1| d x\)
Answer:

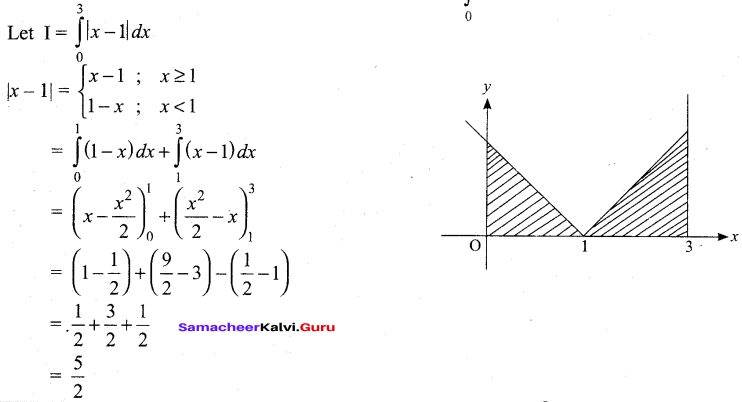
Question 39.
Solve: \(\frac{d y}{d x}\) + 2v cot x = 3x²cosec²x.
Answer:
This is in the form of \(\frac{d y}{d x}\) + Py = Q
P = 2 cot x ; Q = 3x²cosec²x.
∫ Pdx = ∫2 cot x dx = 2 log sin x = log (sin x)²
Integrating factor: e ^∫pdxe ^log(sinx)2 = (sinx)²

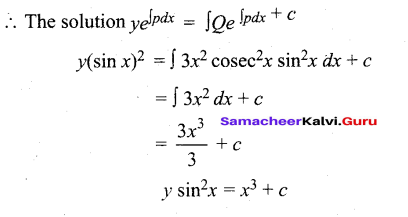
Question 40.
A fair coin is tossed a fixed number of times. If the probability of getting seven heads is
equal to that of getting nine heads, find the probability of getting exactly two heads.
Answer:
p = \(\frac{1}{2}\) q = \(\frac{1}{2}g\)
In binomial distribution
P(X = x) = nC_xp^x q^n-x x = 0, 1, 2,.. . n
By the given data P (X = 7) = P(X = 9)

Part – IV

IV. Answer all the questions. [7 x 5 = 35]

Question 41.
(a) By using Gaussian elimination method, balance the chemical reaction equation:
C₂H₆ → H₂ + CO₂
Answer:
We are searching for positive integers x₁ x₂, x₃ and x₄ such that
x₁ C₂H₆ + x₂O₂ = x₃H₂O + x₄CO₂ …(1)
The number of carbon atoms on LHS of (1) should be equal to number of carbon atoms on the RHS of (1). So we get a linear homogeneous equation.
2x₁ = x₄ ⇒ 2x₁ – x₄ = 0………(2)
Similarly considering hydrogen and oxygen atoms we get respectively.
2x₂ = x₃ + 2x₄
⇒ 2x₂ – x₃ – 2x₄ = 0 ……… (3)
and -2x₃ + 3x₄ = 0 …(4)
Equations (2), (3) and (4) constitute a homogeneous system of linear equations in four unknowns.
The augmented matrix (A,B) is (A,B)

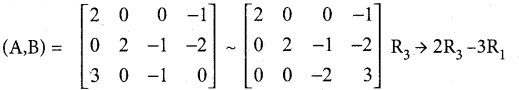
Now p(A, B) = ρ(A) = 3 < number of unknowns. So the system is consistent and has infinite number of solutions. Writing the equations using the echelon form we get
2₁ – x₄ = 0 …(5)
2x₂ – x₃ – 2x₄ = 0 …..(6)
-2x₃ + 3x₄ = 0…..(7)
Taking x₄ = t,(t ≠ 0) in (7) we get
2x₃ – 3t = 0
2x₃ = 3t
\(x_{3}=\frac{3}{2} t\)
Taking x₄ = t, in (5) we get
2₁ – t = 0
2x₁ = t
\(x_{1}=\frac{t}{2}\)

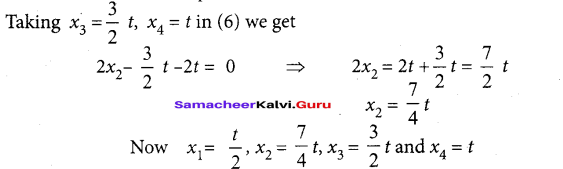
Since x₁ x₂, x₃ and x₄ are positive integers. Let us choose t = 4t.
Then we get x₁ = 2, x₂ = 7, x₃ = 6, and x₄ = 4
So the balanced equation is 2C₂H₆+7O₂
→ 6H₂O + 4CO₂

(b) If z = x + iy and arg \(\left(\frac{z-i}{z+2}\right)=\frac{\pi}{4}\), then show that x² + y² + 3x – 3y + 2 = 0.
Answer:

Question 42.
(a) Solve the equation: 3x⁴ – 16x⁴ + 26x⁴ – 16x + 3 = 0.
Answer:
It is an even degree reciprocal equations
Dividing (1) by x²

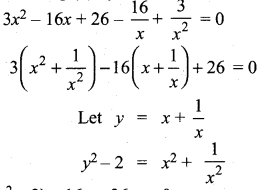
3(y² – 2) – 16y + 26 = 0
3y² – 6 – 16y + 26 = 0
3y² – 16y + 20 = 0
(3y- 10) (y-2) = 0
3y- 10 = 0
3y = 10
3(x + \(\frac{1}{x}\)) = 10
3(x² + 1) = 10x
3x² – 10x + 3=0
(3x- 1) (x- 3) = 0
x = \(\frac{1}{x}\) and x = 3
The roots are 1, 1, \(\frac{1}{3}\), 3
y – 2 = 0
y = 2.
x + \(\frac{1}{x}\) = 2
x² + 1 = 2x
x² – 2x + 1 = 0
(x – 1)² = 0
x = 1,1

OR

(b) Solve: \(\tan ^{-1}\left(\frac{x-1}{x-2}\right)+\tan ^{-1}\left(\frac{x+1}{x+2}\right)=\frac{\pi}{4}\)
Answer:
Tamil Nadu 12th Maths Model Question Paper 5 English Medium – 32

Question 43.
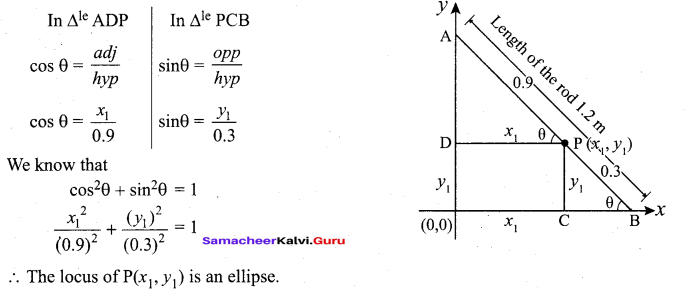
(a) A rod of length 1.2m moves with its ends always touching the coordinates axes. The locus of a point P on the rod, which is 0.3 m from the end in contact with x-axis is an ellipse. Find the eccentricity.
Answer:
From the diagram,
(i)∆^le OAB be a right angle triangle.

are corresponding angles, so corresponding angles are equal.

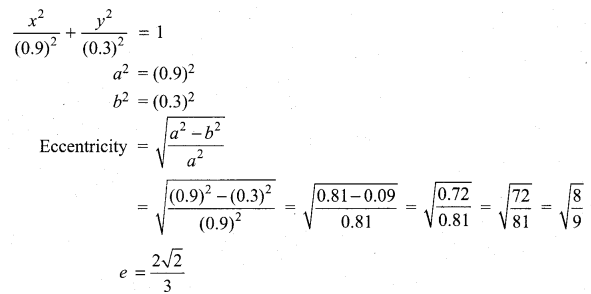
(b) Find the non-parametric and Cartesian equation of the plane passing through the point (4, 2, 4), and is perpendicular to the planes 2jt + 5y + 4z+l = 0 and 4JC + ly T 6z + 2 = 0.
Answer:
The required plane passing through the point (4, 2, 4) and parallel to the vectors

Question 44.
(a) A steel plant is capable of producing JC tonnes per day of a low-grade steel andy tonnes per day of a high-grade steel, where y = \(\frac{40-5 x}{10-x}\) If the fixed market price of low-grade steel is half that of high-grade steel, then what should be optimal productions in low-grade steel and high-grade steel in order to have maximum receipts.
Answer:
Let the price of low-grade steel be ₹p per tonne. Then the price of high-grade steel is ₹2p per tonne.

The total receipt per day is given by R = px + 2py = px + 2p \(\frac{40-5 x}{10-x}\) .
Hence the problem is to maximise R . Now, simplifying and differentiating R with respect to x, we get

and hence R will be maximum. If x = 10 – 2√5 then y = 5 – √5 Therefore the steel plant must produce low-grade and high-grade steels respectively in tonnes per day are 10 -2√5 and 5 – √5 .

[OR]

(b) Let z(x,y) xe^y+ye^x,x = ts²,y = st²,s,t ∈ R.Find \(\frac{\partial z}{\partial s}\) and \(\frac{\partial z}{\partial y}\)
Answer:

Question 45.
(a) Find the area of the region bounded between the parabola x2 = y and the curve
y = |x|.
Answer:
Both the curves are symmetrical about y-axis.
The curve \(y=|x| \text { is } y=\left\{\begin{array}{l}
x \text { if } x \geq 0 \\
-x \text { if } x \leq 0
\end{array}\right.\)
It intersects the parabola x2 = y at (1, 1) and (-1, 1). The area of the region bounded by the curves is sketched in Fig. It lies in the first quadrant as well as in the second quadrant. By symmetry, the required area is twice the area in the first quadrant.
In the first quadrant, the upper curve is y = x,0 ≤ x ≤ 1 and the lower curve is y = x², 0 ≤ x ≤ 1.
Hence, the required area is given by

(b) Water at temperature 100°C cools in 10 minutes to 80°C in a room temperature
of 25°C. Find (i) The temperature of water after 20 minutes (ii) The time when the
temperature is 40°C. [log_e\(\frac{11}{5}\) = -0.3101; log_e5 = 1.6094]
Answer:
Let’T’ be the temperature in time ‘f

Question 46.
(a) Suppose a discrete random variable can only take the values 0,1, and 2.
The probability mass function is defined by \(f(x)=\left\{\begin{array}{cc}
\frac{x^{2}+1}{k}, & \text { for } x=0,1,2 \\
0 & \text { otherwise }
\end{array}\right.\)
Find (i) the value of k (ii) cumulative distribution function (m) P(X ≥ 1).
Answer:

(b) Using truth table check whether the statements \(\neg(\boldsymbol{p} \vee \boldsymbol{q}) \vee \neg(\boldsymbol{p} \wedge \boldsymbol{q}) \text { and } \neg \boldsymbol{p}\) are logically equivalent.
Answer:

Question 47.
(a) Prove by vector method that sin(α + β) = sin α cos β + cos α sin β.
Answer:
Take two points A and B on the unit circle with centre as origin ‘O’, so \(|\overrightarrow{\mathrm{OA}}|=|\overrightarrow{\mathrm{OB}}|=1\)

• Let \(\vec{i}\) and \(\vec{j}\) be the unit vectors along the x, y direction respectively.
• The co-ordinates of A and B be (cos α, sin α) and (cos β, -sin β) respectively.


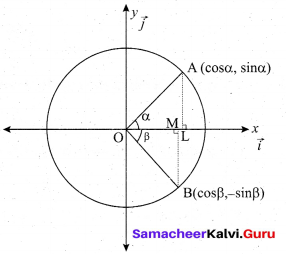
From (1) & (2), we get
sin (α + β) = sin α cos β + cos α sin β

[OR]

(b) Find the equation of tangent and normal to the curve y² – 4x + 2y + 5 = 0 at the point where it cuts the x-axis.
Answer:
y² – 4x + 2y + 5 = 0; given curve cuts the axis, so y = 0
.’. x = \(\frac{5}{4}\)
The required point ( \(\frac{5}{4}\) ,0)

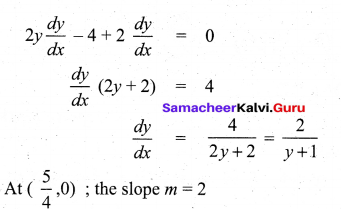
(i) Equation of the tangent

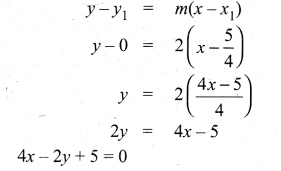
(ii) Equation of the Normal