Students can Download Tamil Nadu 12th Physics Model Question Paper 2 English Medium Pdf, Tamil Nadu 12th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 12th Physics Model Question Paper 2 English Medium
Instructions:
- The question paper comprises of four parts
- You are to attempt all the parts. An internal choice of questions is provided wherever: applicable
- All questions of Part I, II, III and IV are to be attempted separately
- Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
- Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
- Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
- Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Max Marks: 70
PART -1
Answer all the questions. Choose the correct answer. [15 × 1 = 15]
Question 1.
A parallel plate capacitor stores a charge Q at a voltage V. Suppose the area of the parallel plate capacitor and the distance between the plates are each doubled then which is the quantity that will change?
(a) Capacitance
(b) Charge
(c) Voltage
(d) Energy density
Answer:
(d) Energy density
![]()
Question 2.
A carbon resistance has colour bands in order yellow, brown, red. Its resistance is
(a) 41 Ω
(b) 41 × 102 Ω
(c) 4 × 103 Ω
(d) 4.2 Ω
Answer:
(b) 41 × 102 Ω
Question 3.
The magnetic field at the center O of the following
(a) \(\frac{\mu_{0} \mathbf{I}}{4 r} \otimes\)
(b) \(\frac{\mu_{0} I}{4 r} \odot\)
(c) \(\frac{\mu_{0} I}{2 r} \otimes\)
(d) \(\frac{\mu_{0} I}{2 r} \odot\)
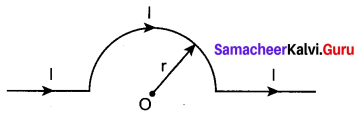
Answer:
(a) \(\frac{\mu_{0} \mathbf{I}}{4 r} \otimes\)
Question 4.
The horizontal component of earth’s magnetic field at a place is 3.6 × 10-5T. If the angle of dip at this place is 60°, the vertical components of earth’s field at this place is
(a) 1.2 × 10-5T
(b) 2.4 × 10-5T
(c) 4 × 10-5T
(d) 6.2 × 10-5T
Hint: Bv = BH tan δ = 3.6 × 10-5 × tan 60°
Bv = 6.2 × 10-5 T
Answer:
(d) 6.2 × 10-5T
Question 5.
In a series RL circuit, the resistance and inductive reactance are the same. Then the phase difference between the voltage and current in the circuit is
(a) \(\frac{\pi}{4}\)
(b) \(\frac{\pi}{2}\)
(c) \(\frac{\pi}{6}\)
(d) zero
Answer:
(a) \(\frac{\pi}{4}\)
![]()
Question 6.
Alternating current can be measured by
(a) moving coil galvanometer
(b) hot wire ammeter
(c) tangent galvanometer
(d) none of the above
Answer:
(b) hot wire ammeter
Question 7.
Let E = E0 sin[106 × -ωt] be the electric field of plane electromagnetic wave, the value of ω is
(a) 0.3 × 10-14 rad s-1
(b) 3 × 10-14 rad s-1
(c) 0.3 × 1014 rad s-1
(d) 3 × 1014 rad s-1
Answer:
(d) 3 × 1014 rad s-1
Question 8.
Two coherent monochromatic light beams of intensities I and 41 are superposed. The maximum and minimum possible intensities in the resulting beam are
(A) 51 and I
(b) 51 and 31
(c) 91 and I
(d) 91 and 31
Answer:
(c) 91 and I
Question 9.
The transverse nature of light is shown in,
(a) interference
(b) diffraction
(c) scattering
(d) polarisation
Answer:
(d) polarisation
![]()
Question 10.
Emission of electrons by the absorption of heat energy is called emission.
(a) photoelectric
(b) field
(c) thermionic
(d) secondary
Answer:
(c) thermionic
Question 11.
Proton and α – particle have the same de-Broglie wavelength. What is same for both of them?
(a) Time period
(b) Energy
(c) Frequency
(d) Momentum
Hint: λ = h/p, when wavelength λ is same, momentum p is also same.
Answer:
(d) Momentum
Question 12.
The ratio of the wavelengths for the transition from n = 2 to n = 1 in Li++, He+ and H is
(a) 1:2: 3
(b) 1:4: 9
(c) 3:2:1
(d) 4: 9: 36
Answer:
(d) 4: 9: 36
Question 13.
The principle in which a solar cell operates
(a) Diffusion
(b) Recombination
(c) Photovoltaic action
(d) Carrier flow
Answer:
(c) Photovoltaic action
Question 14.
The output transducer of the communication system converts the radio signal into
(a) Sound
(b) Mechanical energy
(c) Kinetic energy
(d) None of the above
Answer:
(a) Sound
Question 15.
The alloys used for muscle wires in Robots are
(a) Shape memory alloys
(b) Gold copper alloys
(c) Gold silver alloys
(d) Two dimensional alloys
Answer:
(a) Shape memory alloys
![]()
PART – II
Answer any six questions in which Q. No 22 is compulsory. [6 × 2 = 12]
Question 16.
What is Polarisation?
Answer:
Polarisation \(\overrightarrow{\mathrm{P}}\) is defined as the total dipole moment per unit volume of the dielectric.
\(\overrightarrow{\mathrm{P}}\) = χe \(\overrightarrow{\mathrm{P}}\)ext
Question 17.
Why current is a scalar?
Answer:
The current I is defined as the scalar product of current density and area vector in which the charges cross.
I = \(\overrightarrow{\mathrm{j}}\) . \(\overrightarrow{\mathrm{A}}\)
The dot product of two vector quantity is a scalar form. Hence, current is called as a scalar quantity.
Question 18.
The horizontal component and vertical components of Earth’s magnetic field at a place are 0.15 G and 0.26 G respectively. Calculate the angle of dip and resultant magnetic field.
Answer:
BH = 0.15 G and Bv = 0.26 G
tan I = \(\frac{0.26}{0.15}\) ⇒ I = tan-1 (1.732) = 60°
The resultant magnetic field of the Earth is
\(\mathrm{B}=\sqrt{\mathrm{B}_{\mathrm{H}}^{2}+\mathrm{B}_{\mathrm{H}}^{2}}=0.3 \mathrm{G}\)
Question 19.
State Fleming’s right hand rule.
Answer:
The thumb, index finger and middle finger of right hand are stretched out in mutually perpendicular directions. If the index finger points the direction of the magnetic field and the thumb indicates the direction of motion of the conductor, then the middle finger will indicate the direction of the induced current.
Question 20.
The wavelength of a light is 450 nm. How much phase it will differ for a path of 3 mm?
Answer:
The wavelength is, λ = 450 nm = 450 × 10-9 m
Path difference is, δ = 3 mm = 3 × 10-3 m
Relation between phase difference and path difference is, Φ = \(\frac{2 \pi}{\lambda} \times \delta\)
Substituting, Φ = \(\frac{2 \pi}{450 \times 10^{-9}} \times 3 \times 10^{-3}=\frac{\pi}{75} \times 10^{6}\)
Φ = \(\frac{\pi}{75} \times 10^{6} \mathrm{rad}\)
![]()
Question 21.
How will you define threshold frequency?
Answer:
For a given surface, the emission of photoelectrons takes place only if the frequency of incident light is greater than a certain minimum frequency called the threshold frequency.
Question 22.
Calculate the number of nuclei of carbon-14 undecayed after 22,920 years if the initial number of carbon-14 atoms is 10,000. The half-life of carbon-14 is 5730 years.
Answer:
To get the time interval in terms of half-life, n = \(\frac{t}{\mathrm{T}_{1 / 2}}=\frac{22,920 \mathrm{yr}}{5730 \mathrm{yr}}=4\)
The number of nuclei remaining undecayed after 22,920 years
\(\mathrm{N}=\left(\frac{1}{2}\right)^{n} \mathrm{N}_{0}=\left(\frac{1}{2}\right)^{4} \times 10,000 \Rightarrow \mathrm{N}=625\)
Question 23.
A diode is called as a unidirectional device. Explain
Answer:
Diode is called as a unidirectional device, i.e., current flows in only one direction (anode to cathode internally) when a forward voltage is applied, the diode conducts and when reverse voltage is applied, there is no conduction. A mechanical analogy is a rat chat, which allows motion in one direction only.
Question 24.
Give the factors that are responsible for transmission impairments.
Answer:
- Attenuation
- Distortion (Harmonic)
- Noise
![]()
PART-III
Answer any six questions ¡n which Q.No. 26 ¡s compulsory. (6 × 3 = 18)
Question 25.
A sample of HO gas ¡s placed in a uniform electric field of magnitude 3 × 104 N C-1. The dipole moment of each HCI molecule is 3.4 × 10-30 Cm. Calculate the maximum torque experienced by each HCl molecule.
Answer:
The maximum torque experienced by the dipole is when it is aligned perpendicular to the applied field.
\(\tau_{\max }\) = pE sin90° = 3.4 × 10-30 × 3 × 104Nm
\(\tau_{\max }\) =10.2 × 10-26Nm
Question 26.
The resistance ola wire is 20 Ω . What will be new resistance, ¡fit is stretched uniformly 8 times its original length?
Answer:
R1 = 20 Ω, R2 = ?
Let the original length (l1) be 1.
The new length, l2 = 8l1 (i.,e) l2 =8l
The original resistance,
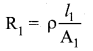
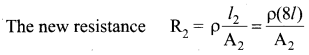
Though the wire is stretched, its volume is unchanged.
Initial volume = Final volume
A1l1 = A2l2 , A1l =A28l
\(\frac{A_{1}}{A_{2}}=\frac{8 l}{l}=8\)
By dividing equation R2 by equation R1, we get
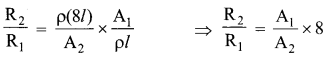
Substituting the value of \(\frac{A_{1}}{A_{2}}\) we get
\(\frac{R_{1}}{R_{2}}\) = 8 × 8 = 64 ⇒ R2 = 64 × 20 = 1280 Ω
Hence, strecthing the length of the wire has increased its resistance.
Question 27.
State Biot-Savart’s law.
The magnitude of magnetic field \(d \vec{B}\) at a point P at a distance r from the small elemental length taken on a conductor carrying current varies
- directly as the strength of the current I
- directly as the magnitude of the length element \(d \vec{l}\)
- directly as the sine of the angle (say,0) between d\(d \vec{l}\) and r̂ .
- inversely as the square of the distance between the point P and length element \(d \vec{l}\).
This is expressed as
\(d \mathrm{B} \propto \frac{\mathrm{I} d l}{r^{2}} \sin \theta\)
![]()
Question 28.
Give the principle of AC generator.
Answer:
Alternators work on the principle of electromagnetic induction. The relative motion between a conductor and a magnetic field changes the magnetic flux linked with the conductor which in turn, induces an emf. The magnitude of the induced emf is given by Faraday’s law of electromagnetic induction and its direction by Fleming’s right hand rule.
Question 29.
A transformer is used to light a 140 W, 24 V bulb from a 240 V AC mains. The current in the main cable is 0.7 A. Find the efficiency of the transformer.
Answer:
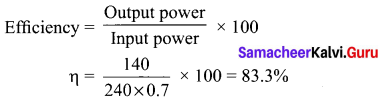
Question 30.
What are the Cartesian sign conventions for a spherical mirror?
Answer:
- The Incident light is taken from left to right (i.e. object on the left of mirror).
- All the distances are measured from the pole of the mirror (pole is taken as origin).
- The distances measured to the right of pole along the principal axis are taken as positive.
- The distances measured to the left of pole along the principal axis are taken as negative,
- Heights measured in the upward perpendicular direction to the principal axis are taken as positive.
- Heights measured in the downward perpendicular direction to the principal axis, are taken as negative.
Question 31.
Write the relationship of de Broglie wavelength k associated with a particle of mass m in terms of its kinetic energy K.
Answer:
Kinetic energy of the particle, K = \(\frac{1}{2}\) mv2 = \(\frac{p^{2}}{2 m}\)
p = \(\sqrt{2 m \mathrm{K}}\)
de-Broglie wavelength of the particle λ = \(\frac{h}{p}=\frac{h}{\sqrt{2 m \mathrm{K}}}\)
Question 32.
What is binding energy of a nucleus? Give its expression.
Answer:
when Z protons and N neutrons combine to form a nucleus, mass equal to mass defect disappears and the corresponding energy is released. This is called the binding energy of the nucleus (BE) and is equal to (Δm)c2 .
BE = (Zmp + Nmn – M ) c2
Question 33.
Distinguish between avalanche and zener breakdown.
Answer:
|
Avalanche Breakdown |
Zener Breakdown |
| It occurs injunctions which are lightly and have wide depletion widths. | It occurs injunctions which are heavily doped and have narrow depletion widths. |
| It occurs at higher reverse voltages when thermally generated electrons get enough kinetic energy to produce more electrons by collision. | It occurs due to rupture of covalent bonds by strong electric fields set up in depletion region by the reverse voltage. |
| At reverse voltage above 6V breakdown is due to avalanche effect. | At reverse voltage below 6V breakdown is due to zener effect. |
| Electric field produced is weak in nature. | A strong electric field is produced |
| Charge carriers obtain energy from the applied potential. | Zener current is independent of applied voltage. |
![]()
PART – IV
Answer all the questions. [5 × 5 = 25]
Question 34.
(a) Calculate the electric field due to a dipole on its axial line and equatorial plane.
Answer:
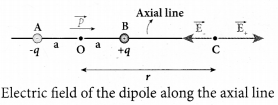
Case (i) Electric field due to an electric dipole at points on the axial line. Consider an electric dipole placed on the x-ax is as shown in figure. A point C is located at a distance of r from the midpoint O of the dipole along the axial line. line
The electric field at a point C due to +q is
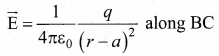
Since the electric dipole moment vector \(\vec{p}\) is from -q to +q and is directed along BC, the above equation is rewritten as

where P̂ is the electric dipole moment unit vector from -q to +q.
The electric field at a point C due to -q is

Since +q is located closer to the point C than -q, \(\vec{E}\)– \(\vec{E}\)+ us stronger than \(\vec{E}\)–. Therefore, the length of the \(\vec{E}\)+ vector is drawn large than that of \(\vec{E}\)– vector.
The total electric field at point C is calculated using the superposition principle of the electric field.
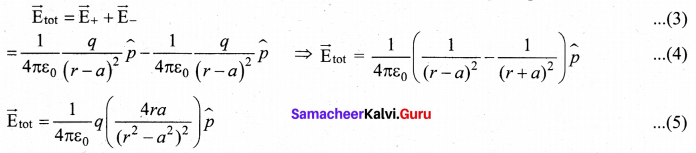
Note that the total electric field is along \(\vec{E}\)+ since +q is closer to C than -q.
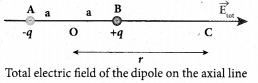
The direction of \(\vec{E}\)tot is shown in Figure
If the point C is very far away from the dipole then (r >> a).
Under this limit the term(r2 – a2) ≈ r4 Substituting this into equation, we get

If the point C is chosen on the left side of the dipole, the total electric field is still in the direction of \(\vec{p}\).
Case (ii) Electric field due to an electric dipole at a point on the equatorial plane
Consider a point C at a distance r from the midpoint O of the dipole on the equatorial plane as shown in Figure. Since the point C is quite-distant from +q and -q, the magnitude of the electric fields of +q and -q are the same. The direction of E is along BC and the direction of \(\vec{E}\)+ is along and the direction of \(\vec{E}\)– CA. \(\vec{E}\)+ and \(\vec{E}\)– are resolved into two components; one component parallel to the dipole axis and the other perpendicular to it. The perpendicular components \(\left|\overrightarrow{\mathrm{E}}_{+}\right|\) sin θ and \(\left|\overrightarrow{\mathrm{E}}_{-}\right| sin θ\) are oppositely directed and cancel each other. The magnitude of the total electric field at point C is the sum of the parallel components of \(\vec{E}\)+ and \(\vec{E}\)– and its direction is along -P̂
![]()
The magnitudes \(\vec{E}\)+ and \(\vec{E}\)– are the same and are given by
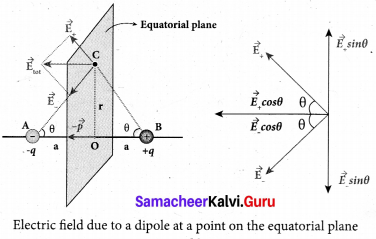
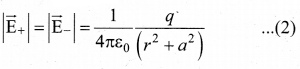
By substituting equation (1) into equation (2), we get

![]()
Question 34.
(b) Obtain the condition for bridge balance in Wheatstone’s bridge.
Answer:
An important application of Kirchhoff’s rules is the Wheatstone’s bridge. It is used to compare resistances and also helps in determining the unknown resistance in electrical network. The bridge consists of four resistances P, Q, R and S connected, A galvanometer G is connected between the points B and D. The battery is connected between the points A and C. The current through the galvanometer is IG and its resistance is G.
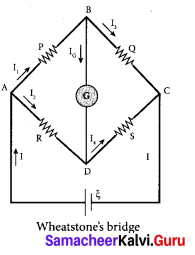
Applying Kirchhoff’s current rule to junction B,
I1 – IG – I3 = 0 ……. (1)
Applying Kirchhoff’s current rule to junction D,
I2 + IG – I4 = 0 ……. (2)
Applying Kirchhoff’s voltage rule to loop ABDA,
I1p + IGG – I2R = 0 ……. (3)
Applying Kirchhoff’s voltage rule to loop ABCDA,
I1p – I3Q – I4S – I2R = 0 ……. (4)
When the points B and D are at the same potential, the bridge is said to be balanced. As there is no potential difference between B and D, no current flows through galvanometer (IG = 0).
Substituting IG = O in equation, (I), (2) and (3), we get
I1 = I3 …… (5)
I2 = I4 ……… (6)
I1p = I2R ………. (7)
Substituting the equation (5) and (6) in equation (4)
I1P + I1Q – I2S – I2R= 0
I1(P + Q) = I2(R+S) …… (8)
Dividing equation (8) By equation (7), we get
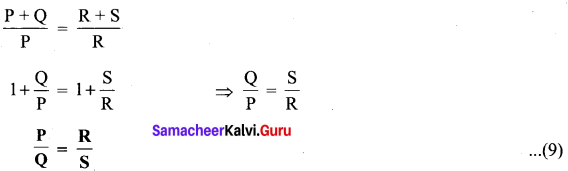
This is the bridge balance condition. Only under this condition, galvanometer shows null deflection. Suppose we know the values of two adjacent resistances, the other two resistances can be compared. If three of the resistances are known, the value of unknown resistance (fourth one) can be determined.
![]()
Question 35.
(a) Show the time period of oscillation when a bar magnet is kept in a uniform magnetic field is T = 2π\(\sqrt{\frac{1}{p_{m} \mathrm{B}}}\). in second, where I represents moment of interia of the bar magnet, p<sub<m is the magnetic moment and is the magnetic field.
Answer:
The magnitude of deflecting torque (the torque which makes the object rotate) acting on the bar magnet which will tend to align the bar magnet parallel to the direction of the uniform magnetic field \(\overrightarrow{\mathrm{B}}\) is
\(\vec{\tau}\) = pm B sin θ
The magnitude of restoring torque acting on the bar magnet can be written as
\(|\vec{\tau}|=\mathrm{I} \frac{d^{2} \theta}{d t^{2}}\)
Under equilibrium conditions, both magnitude of deflecting torque and restoring torque will be equal but act in the opposite directions, which means
\(\mathrm{I} \frac{d^{2} \theta}{d t^{2}}=-p_{m} \mathrm{B} \sin \theta\)
The negative sign implies that both are in opposite directions. The above equation can be written as
\(\frac{d^{2} \theta}{d t^{2}}=-\frac{p_{m} B}{I} \sin \theta\)
This is non-linear second order homogeneous differential equation. In order to make it linear, we use small angle approximation, i.e., sin θ ≈ θ, we get
\(\frac{d^{2} \theta}{d t^{2}}=-\frac{p_{m} \mathrm{B}}{\mathrm{I}} \theta\)
This linear second order homogeneous differential equation is a Simple Harmonic differential equation. Therefore,
Comparing with Simple Harmonic Motion (SHM) differential equation \(\frac{d^{2} x}{d t^{2}}=-\omega^{2} x\)
where ω is the angular frequency of the oscillation.
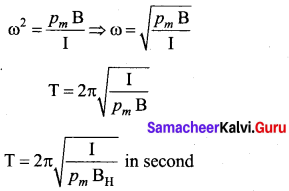
where, BH is the horizontal component of Earth’s magnetic field.
[OR]
Question 35.
(b) An inductor of inductance L carries an electric current i. How much energy is stored while establishing the current in it?
Answer:
Energy stored in an inductor: Whenever a current is established in the circuit, the inductance opposes the growth of the current. In order to establish a current in the circuit, work is done against this opposition by some external agency. This work done is stored as magnetic potential energy. Let us assume that electrical resistance of the inductor is negligible and inductor effect alone is considered. The induced emf eat any instant t is
ℰ = \(-\mathrm{L} \frac{d i}{d t}\) …(1)
Let dW be work done in moving a charge dq in a time dt against the opposition, then
dW = -edq = -ℰdq = -ℰidi [ ∵ dq = idt]
Substituting for e value from equation (1)
= \(-\left(-\mathrm{L} \frac{d i}{d t}\right) i d t\)
dW = Lidt ……. (2)
Total work done in establishing the current i is
This work done is stored as magnetic potential energy.
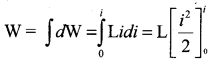
W = \(\frac{1}{2}\) Li2 ………. (3)
This work done is stored as magnetic potential energy.
∴ UB = \(\frac{1}{2}\) Li2
![]()
Question 36.
(a) Using Faraday’s law of electromagnetic induction, derive an equation for motional emf.
Answer:
Motional emf from Faraday’s law: Let us consider a rectangular conducting loop of width l in a uniform magnetic field \(\overrightarrow{\mathrm{B}}\) which is perpendicular to the plane of the loop and is directed inwards. A part of the loop is in the magnetic field while the remaining part is outside the field.
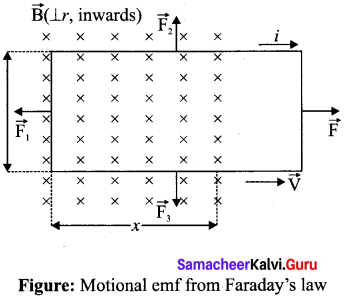
When the loop is pulled with a constant velocity \(\overrightarrow{\mathrm{v}}\) to the right, the area of the portion of the loop within the magnetic field will decrease. Thus, the flux linked with the loop will also decrease. According to Faraday’s law, an electric current is induced in the loop which flows in a direction so as to oppose the pull of the loop.
Let x be the length of the loop which is still within the magnetic field, then its area is lx. The magnetic flux linked with the loop is
ΦB = \(\int_{A} \vec{B} \cdot d \vec{A}=B A \cos \theta\)
Here θ = 0° and cos 0° = 1
= BA
ΦB = Blx ……… (1)
As this magnetic flux decreases due to the movement of the loop, the magnitude of the induced emf is given by
\(\varepsilon=\frac{d \Phi_{\mathrm{B}}}{d t}=\frac{d}{d t}(\mathrm{B} l x)\)
Here, both B and l are constants. Therefore,
\(\varepsilon=\mathrm{B} l \frac{d x}{d t}=\mathrm{B} l v\) …… (2)
where v = \(\frac{d x}{d t}\) is the velocity of the loop. This emf is known as motional emf since it is produced due to the movement of the loop in the magnetic field.
![]()
[OR]
Question 36.
(b) Derive the mirror equation and the equation for lateral magnification. The mirror equation:
Answer:
The mirror equation establishes a relation among object distance u, image distance v and focal length/for a spherical mirror. An object AB is considered on the principal axis of a concave mirror beyond the center of curvature C.
Let us consider three paraxial rays from point B on the object.
The first paraxial ray BD travelling parallel to principal axis is incident on the concave mirror at D, close to the pole P. After reflection the ray passes through the focus F. The second paraxial ray BP incident at the pole P is reflected along PB’. The third paraxial ray BC passing through centre of curvature C, falls normally on the mirror at E is reflected back along the same path.
The three reflected rays intersect at the point B’. A perpendicular drawn as A’ B’ to the principal axis is the real, inverted image of the object AB.
As per law of reflection, the angle of incidence ∠BPA is equal to the angle of reflection ∠B’PA’ . The triangles ∆BPA and ∆B’PA’ are similar. Thus, from the rule of similar triangles,
\(\frac{A^{\prime} B^{\prime}}{A B}=\frac{P A^{\prime}}{P A}\) …… (1)
The other set of similar triangles are, ∆DPF and ∆ BA.’ F. (PD is almost a straight vertical line)
\(\frac{A^{\prime} B^{\prime}}{P D}=\frac{A^{\prime} F}{P F}\)
As, the distances PD = AB the above equation becomes,
\(\frac{A^{\prime} B^{\prime}}{A B}=\frac{A^{\prime} F}{P F}\) …….. (2)
From equations (1) and (2) we can write,
\(\frac{P A^{\prime}}{P A}=\frac{A^{\prime} F}{P F}\)
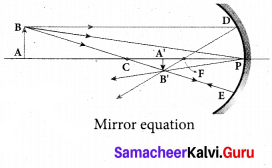
As, A’ F PA’ – PF, the above equation becomes,
\(\frac{P A^{\prime}}{P A}=\frac{P A^{\prime}-P F}{P F}\)
We can apply the sign conventions for the various distances in the above equation.
PA= -u. PA’= -v, PF = -f
All the three distances are negative as per sign convention, because they are measured to the left of the pole. Now, the equation (3) becomes.

The above equation (4) is called mirror equation
Lateral magnification in spherical mirrors:
The lateral or transverse magnification is defined as the ratio of the height of the image to the height of the object. The height of the object and image are measured perpendicular to the principal axis.
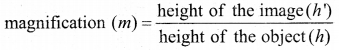
m = \(\frac{h^{\prime}}{h}\) …… (5)
Applying proper sign conventions for equation (1), A’B’ PA’
\(\frac{A^{\prime} B^{\prime}}{A B}=\frac{P A^{\prime}}{P A}\)
A’B’ = -h, AB = h, PA’ = -v, PA = -u
\(\frac{-h^{\prime}}{h}=\frac{-v}{-u}\)
On simplifying we get,
\(m=\frac{h^{\prime}}{h}=-\frac{v}{u}\) …….(6)
Using mirror equation, we can further write the magnification as,
\(m=\frac{h^{\prime}}{h}-\frac{f-v}{f}=\frac{f}{f-u}\) ……… (7)
![]()
Question 37.
(a) Obtain Einstein’s photoelectric equation with necessary explanation.
Answer:
Einstein’s explanation of photoelectric equation:
When a photon of energy hv is incident on a metal surface, it is completely absorbed by a single electron and the electron is ejected.
In this process, a part of the photon energy is used for the ejection of the electrons from the metal surface (photoelectric work function Φ0) and the remaining energy as the kinetic energy of the ejected electron. From the law of conservation of energy,
hυ = Φ0 + \(\frac { 1 }{ 2 }\) mv2 …… (1)
where m is the mass of the electron and u its velocity
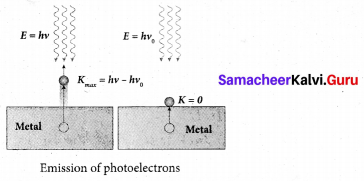
If we reduce the frequency of the incident light, the speed or kinetic energy of photo electrons is also reduced. At some frequency v0 of incident radiation, the photo electrons are ejected with almost zero kinetic energy. Then the equation (1) becomes
hυ0 = Φ0
where v0 is the threshold frequency. By rewriting the equation (1), we get
hυ = hυ0 + \(\frac { 1 }{ 2 }\) mv2 …….(2)
The equation (2) is known as Einstein’s Photoelectric equation.
If the electron does not lose energy by internal collisions, then it is emitted with maximum kinetic energy Kmax. Then
Kmax = \(\frac { 1 }{ 2 }\) mv2max
where υmax is the maximum velocity of the electron ejected. The equation (1) is rearranged as follows:
Kmax = hυ – Φ0
![]()
[OR]
Question 37.
(b) Derive the energy expression for hydrogen atom using Bohr atom model.
Answer:
The energy of an electron in the nth orbit
Since the electrostatic force is a conservative force, the potential energy for the orbit is
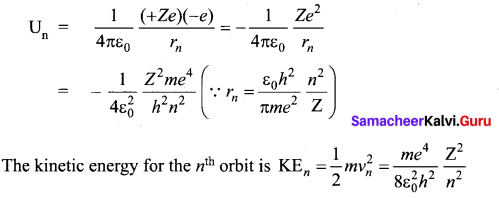
This implies that Un = -2 KEn. Total energy in the «th orbit is
En = KEn + Un = KEn – 2KEn = -KEn
En = \(-\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{2}} \frac{Z^{2}}{n^{2}}\)
For hydrogen atom (Z = 1),
En = \(\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{2}} \frac{1}{n^{2}} \text { joule }\) ……. (1)
where n stands for principal quantum number. The negative sign in equation (1) indicates that the electron is bound to the nucleus.
Substituting the values of mass and charge of an electron (m and e), permittivity of free space s0 and Planck’s constant h and expressing in terms of eW. we get
En = -13.6\(\frac{1}{n^{2}}\)eV
For the first orbit (ground state), the total energy of electron is E1 = – 13.6 eV. For the second orbit (first excited state), the total energy of electron is E2 = -3.4 eV. For the third orbit (second excited state), the total energy of electron is E3 =1.51 eV and so on.
Notice that the energy of the first excited state is greater than the ground state, second excited state is greater than the first excited state and so on. Thus, the orbit which is closest to the nucleus (r1) has lowest energy (minimum energy compared with other orbits). So, it is often called ground state energy (lowest energy state). The ground state energy of hydrogen (-13.6 eV ) is used as a unit of energy called Rydberg (1 Rydberg = -13.6 eV ).
The negative value of this energy is because of the way the zero of the potential energy is defined. When the electron is taken away to an infinite distance (very far distance) from nucleus, both the potential energy and kinetic energy terms vanish and hence the total energy also vanishes.
Question 38.
(a) Explain the construction and working of a full wave rectifier.
Full wave rectifier:
The positive and negative half cycles of the AC input signal pass through the full wave rectifier circuit and hence it is called the full wave rectifier. It consists of two p-n junction diodes, a center tapped transfonner, and a load resistor (RL). The centre is usually taken as the ground or zero voltage reference point. Due to the centre tap transformer, the output voltage rectified by each diode is only one half of the total secondary voltage.
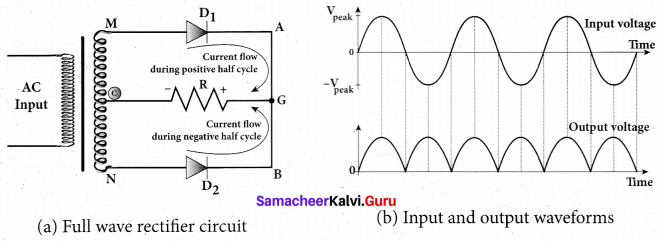
During positive half cycle:
When the positive half cycle of the ac input signal passes through the circuit, terminal M is positive, G’ is at zero potential and N is at negative potential. This forward biases diode D1 and reverse biases diode D2 Hence, being forward biased, diode D1 conducts and current flows along the path MD1 AGC . As a result, positive half cycle of the voltage appears across RL in the direction G to C.
During negative half cycle:
When the negative half cycle of the ac input signal passes through the circuit, terminal N is positive, G is at zero potential and M is at negative potential. This forward biases diode D2 and reverse biases diode D1. Hence, being forward biased, diode D2 conducts and current flows along the path ND2 BGC . As a result, negative half cycle of the voltage appears across RL in the same direction from G to C
Hence in a full wave rectifier both positive and negative half cycles of the input signal pass through the circuit in the same direction as shown in figure (b). Though both positive and negative half cycles of ac input are rectified, the output is still pulsating in nature.
The efficiency ( η) of full wave rectifier is twice that of a half wave rectifier and is found to be 81.2 %. It is because both the positive and negative half cycles of the ac input source are rectified.
![]()
[OR]
Question 38.
(b) Give the applications of ICT in mining and agriculture sectors.
Answer:
(i) Agriculture
The implementation of information and communication technology (ICT) in agriculture sector enhances the productivity, improves the living standards of farmers and overcomes the challenges and risk factors.
(a) ICT is widely used in increasing food productivity and farm management.
(b) It helps to optimize the use of water, seeds and fertilizers etc.
(c) Sophisticated technologies that include robots, temperature and moisture sensors, aerial images, and GPS technology can be used.
(d) Geographic information systems are extensively used in farming to decide the suitable place for the species to be planted.
(ii) Mining
(a) ICT in mining improves operational efficiency, remote monitoring and disaster locating system.
(b) Information and communication technology provides audio-visual warning to the trapped underground miners.
(c) It helps to connect remote sites.