Tamil Nadu 12th Physics Model Question Paper 4 English Medium

Students can Download Tamil Nadu 12th Physics Model Question Paper 4 English Medium Pdf, Tamil Nadu 12th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 12th Physics Model Question Paper 4 English Medium

Instructions:

1. The question paper comprises of four parts
2. You are to attempt all the parts. An internal choice of questions is provided wherever: applicable
3. All questions of Part I, II, III and IV are to be attempted separately
4. Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each.  These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
6. Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
7. Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.

Time: 3 Hours
Max Marks : 70

PART -1

Answer all the questions. Choose the correct answer. [15 × 1 = 15]

Question 1.
Two identical conducting balls having positive charges q₁ and q₂ are separated by a center to center distance r. If they are made to touch each other and then separated to the same distance, the force between them will be …………………… .
(a) less than before
(b) same as before
(c) more than before
(d) zero
Answer:
(c) more than before

Question 2.
Two plates are 1 cm apart and the potential difference between them is 10 V. The electric field between the plates is …………………. .
(a) 10 NC^-1
(b) 250 NC^-1
(c) 500 NC^-1
(d) 1000 NC^-1
Hint: E = \(\frac{V}{d}=\frac{10}{1 \times 10^{-2}}\) = 1000 NC^-1
Answer:
(d) 1000 NC^-1

Question 3.
A toaster operating at 240 V has a resistance of 120 Ω. The power is ………………… .
(a) 400 W
(b) 2 W
(c) 480 W
(d) 240 W
Answer:
(c) 480 W

Question 4.
Three wires of equal lengths are bent in the form of loops. One of the loops is circle, another is a semi-circle and the third one is a square. They are placed in a uniform magnetic field and same electric current is passed through them. Which of the following loop configuration will experience greater torque ?
(a) circle
(b) semi-circle
(c) square
(d) all of them
Answer:
(a) circle

Question 5.
A bar magnet of magnetic moment M is cut into two parts of equal length. The magnetic moment of either part is ………………….. .
(a) M
(b) 2M
(c) \(\frac{M}{2}\)
(d) Zero
Answer:
(c) \(\frac{M}{2}\)

Question 6.
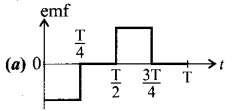
The current flowing in a coil varies with time as shown in ® the figure. The variation of induced emf with time would be …………….. .


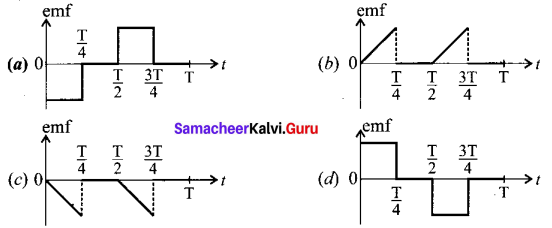
Answer:

Question 7.
Which of the following electromagnetic radiation is used for viewing objects through fog?
(a) microwave
(b) gamma rays
(c) X- rays
(d) infrared
Answer:
(d) infrared

Question 8.
Stars twinkle due to …………………. .
(a) reflection
(b) total internal reflection
(c) refraction
(d) polarisation
Answer:
(c) refraction

Question 9.
When a plane electromagnetic wave enters a glass slab, then which of the following will not change?
(a) Wavelength
(b) Frequency
(c) Speed
(d) Amplitude
Hint: Only the frequency of the electromagnetic wave remains unchanged.
Answer:
(b) Frequency

Question 10.
In an electron microscope, the electrons are accelerated by a voltage of 14 kV. If the voltage is changed to 224 kV, then the de Broglie wavelength associated with the electrons would …………………… .
(a) increase by 2 times
(b) decrease by 2 times
(c) decrease by 4 times
(d) increase by 4 times
Hint: At Voltage, V = 14 kV
de-Broglie wavelength of electron, λ = \(\frac{12.3}{\sqrt{14000}}\) Å = 0.104 Å
At voltage, V = 224 kV
λ’ = \(\frac{12.3}{\sqrt{224000}}\) Å = 0.026 Å
\(\frac{\lambda}{\lambda^{\prime}}=\frac{0.104}{0.0260}\) = 4 ⇒ λ = 4λ’ ⇒ λ’ = \(\frac{\lambda}{4}\)
Answer:
(c) decrease by 4 times

Question 11.
The charge of cathode rays is …………………. .
(a) positive
(b) negative
(c) neutral
(d) not defined
Answer:
(a) positive
(b) negative

Question 12.
The primary use of a zener diode is …………………… .
(a) Rectifier
(b) Amplifier
(c) Oscillator
(d) Voltage regulator
Answer:
(d) Voltage regulator

Question 13.
For a common base circuit if \(\frac{I_{C}}{I_{E}}\) = 0.98, then current gain for common emitter circuit will be ………………. .
(a) 49
(b) 98
(c) 4.9
(d) 25.5
Ir a 0 98

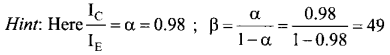
Answer:
(a) 49

Question 14.
The internationally accepted frequency deviation for the purpose of FM broadcasts.
(a) 75 kHz
(b) 68 kHz
(c) 80 kHz
(d) 70 kHz
Answer:
(a) 75 kHz

Question 15.
“Sky wax” is an application of nano product in the field of …………………….. .
(a) Medicine
(b) Textile
(c) Sports
(d) Automotive industry
Answer:
(c) Sports

PART – II

Answer any six questions. Question No. 23 is compulsory. [6 × 2 = 12]

Question 16.
The electric field lines never intersect. Justify.
Answer:
As a consequence, if some charge is placed in the intersection point, then it has to move in two different directions at the same time, which is physically impossible. Hence, electric field lines do not intersect.

Question 17.
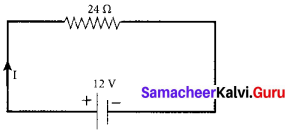
A potential difference across 24 ft resistor is 12 V. What is the current through the resistor?
Answer:
V = 12 V
and R = 24 Ω
Current, I = ?
From Ohm’s law, \(I=\frac{V}{R}=\frac{12}{24}=0.5 \mathrm{A}\)

Question 18.
State Coulomb’s inverse law.
Answer:
The force of attraction or repulsion between two magnetic poles is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between ‘ them.
\(\overrightarrow{\mathrm{F}} \propto \frac{q_{m_{\mathrm{A}}} q_{m_{b}}}{r^{2}} \hat{r}\)

Question 19.
State Lenz’s law.
Answer:
Lenz’s law states that the direction of the induced current is such that it always opposes the cause responsible for its production.

Question 20.
What is angle of deviation due to reflection?
Answer:
The angle between the incident and deviated light ray is called angle of deviation of the light ray. It is written as, d = 180 – (i + r). As, i = r in reflection, we can write angle of deviation in  reflection at plane surface as. d = 180 – 2i

Question 21.
What is photoelectric effect?
Answer:
The ejection of electrons from a metal plate when illuminated by light or any other electromagnetic radiation of suitable wavelength (or frequency) is called photoelectric effect.

Question 22.
Define impact parameter.
Answer:
The impact parameter is defined as the perpendicular distance between the centre of the gold nucleus and the direction of velocity vector of alpha particle when it is at a large distance.

Question 23.
In a transistor connected in the common base configuration, α = 0.95, I_E = mA. Calculate the values of I_c and I_B
Answer:
α = \(\frac{\mathrm{I}_{\mathrm{C}}}{\mathrm{I}_{\mathrm{E}}}\)
I_c = αI_E = 0.95 × 1 = 0.95 mA
I_E = I_B + I_c
∴ I_B = I_c – I_E = 1 – 0.95 = 0.05 mA

Question 24.
What do you mean by Internet of Things?
Answer:
Internet of Things (IoT), it is made possible to control various devices from a single device. Example: home automation using a mobile phone.

PART-III

Answer any six questions. Question No. 28 is compulsory. [6 × 3 = 18]

Question 25.
Write down Coulomb’s law in vector form and mention what each term represents.
Answer:
The force on a charge q₁ exerted by a point charge q₂ is given by
\(\overrightarrow{\mathrm{F}}_{12}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}} \hat{r}_{21}\)
Here r̂₂₁ is the unit vector from charge q₂ to q₁
But r̂₂₁ = -r̂₂₁

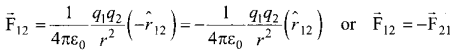
Therefore, the electrostatic force obeys Newton’s third law.

Question 26.
Write down the various forms of expression for power in electrical circuit.
Answer:
The electric power P is the rate at which the electrical potential energy is delivered,
\(P=\frac{d U}{d t}=\frac{1}{d t}(V \cdot d Q)=V \cdot \frac{d Q}{d t}\)
[dU = V.dQ]
The electric power delivered by the battery to any electrical system.
P = VI
The electric power delivered to the resistance R is expressed in other forms.
P = VI = I(IR) = I²R
P = IV = \(\left(\frac{V}{R}\right) V=\frac{V^{2}}{R}\)

Question 27.
The repulsive force between two magnetic poles in air is 9 × 10^-3 N. If the two poles are equal in strength and are separated by a distance of 10 cm, calculate the pole strength of each pole.
Answer:
The force between two poles are given by \(\overrightarrow{\mathrm{F}}=k \frac{q_{m_{\mathrm{A}}} q_{m_{\mathrm{B}}}}{r^{2}}\)
The magnitude of the force is F = \(F=k \frac{q_{m_{A}} q_{m_{B}}}{r^{2}}\)
Given : F = 9 × 10^-3 N, r = 10 cm = 10 × 10^-2 m
Therefore 9 × 10^-3 = 10^-7 × \(\frac{q_{m}^{2}}{\left(10 \times 10^{-2}\right)^{2}}\) ⇒ q_m = 30NT^-1

Question 28.
A 200 turn coil of radius 2 cm is placed co-axially within a long solenoid of 3 cm radius. If the turn density of the solenoid is 90 turns per cm, then calculate mutual inductance of the coil.
Answer:
Numbef of turns of the solenoid, N₂ = 200
Radius of the solenoid, r cm = 2 × 10^-2 m
Area of the solenoid, A = πr² = 3.14 × (2 × 10^-2)^-2 = 1.256 × 10^-3 m²
Turn density of long solenoid per cm, N₁ = 90 × 10²

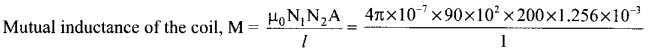
= 283956.48 × 10^-8 ⇒ M = 2.84 mH

Question 29.
Compute the speed of the electromagnetic wave in a medium if the amplitude of electric and magnetic fields are 3 × 10⁴ N C^-1 and 2 × 10^-4 T, respectively.
Answer:
The amplitude of the electric field, E₀ = 3 × 10⁴ N C^-1.
The amplitude of the magnetic field, B_o = 2 × 10^-4 T. Therefore, speed of the electromagnetic wave in a medium is
\(v=\frac{3 \times 10^{4}}{2 \times 10^{-4}}=1.5 \times 10^{8} \mathrm{ms}^{-1}\)

Question 30.
State the laws of refraction.
Answer:
Law of refraction is called Snell’s law.
Snell’s law states that,
(a) The incident ray, refracted ray and normal to the refracting surface are all coplanar (i.e. lie in the same plane).
(b) The ratio of angle of incident i in the first medium to the angle of reflection r in the second medium is equal to the ratio of refractive index of the second medium n₂ to that of the refractive index of the first medium n₁.
\(\frac{\sin i}{\sin r}=\frac{n_{2}}{n_{1}}\)

Question 31.
A proton and an electron have same de Broglie wavelength. Which of them moves faster and which possesses more kinetic energy?
Answer:
We know that λ = \(\frac{h}{\sqrt{2 m K}}\)
Since proton and electron have same de Broglie wavelength, we get

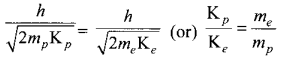
Since m_e < m_p , K_p < K_e, the electron has more kinetic energy than the proton.

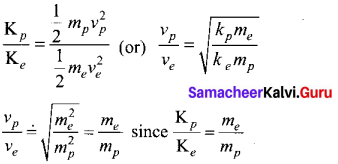
Since m_e < m_p ν_p < ν_e , the electron moves faster than the proton.

Question 32.
In alpha decay, why the unstable nucleus emits ⁴₂He nucleus? Why it does not emit four separate nucleons?
Answer:
After all ⁴₂He consists of two protons and two neutrons. For example, if ²³⁸₉₂U nucleus decays into ²³⁴₉₀Th by emitting four separate nucleons (two protons and two neutrons), then the disintegration energy Q for this process turns out to be negative. It implies that the total mass of products is greater than that of parent (²³⁸₉₂U) nucleus. This kind of process cannot occur in nature because it would violate conservation of energy. In any decay process, the conservation of energy, conservation of linear momentum and conservation of angular momentum must be obeyed.

Question 33.
Distinguish between intrinsic and extrinsic semiconductors.
Answer:

Intrinsic semiconductors	Extrinsic semiconductors
These are pure semiconducting tetravalent crystals.	These are semiconducting tetravalent crystals doped with impurity atoms group III (or) V
Their electrical conductivity is low.	Their electrical conductivity is high.
There is no permitted energy state between valence and conduction band.	There is no permitted energy state of the impurity atom between valence and conduction band.
Their electrical conductivity depends on temperature.	Their electrical conductivity depends on temperature as well as dopant concentration.

PART – IV

Answer all the questions. [5 × 1 = 5]

Question 34.
(a) Derive an expression for electrostatic potential due to an electric dipole.
Answer:
Electrostatic potential at a point due to an electric dipole: Consider two equal and opposite charges separated by a small distance 2a. The point P is located at a distance r from the midpoint of the dipole. Let θ be the angle between the line OP and dipole axis AB.
Let r₁ be the distance of point P from +q and r₂ be the distance of point P from -q.
Potential at P due to charge +q = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r_{1}}\)
Potential at P due to charge -q = \(-\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r_{2}}\)
Total potential at the point P,
V = \(\frac{1}{4 \pi \varepsilon_{0}} q\left(\frac{1}{r_{1}}-\frac{1}{r_{2}}\right)\) ……… (1)
Suppose if the point P is far away from the dipole, such that r>>a, then equation can be expressed in terms of r. By the cosine law for triangle BOP,

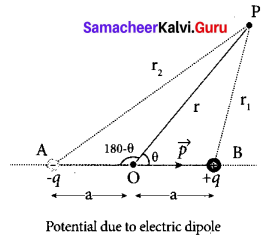
r²₁ = r² + a² – 2ra cos θ = r²\(\left(1+\frac{a^{2}}{r^{2}}-\frac{2 a}{r} \cos \theta\right)\)

Since the point P is very far from dipole, then r >> a. As a result the term \(\frac{a^{2}}{r^{2}}\) is very small and can be neglected. Therefore

since \(\frac{a}{r}\)<< 1, we can use binominal theorem and retain the terms up to first order r
\(\frac{1}{r_{1}}=\frac{1}{r}\left(1+\frac{a}{r} \cos \theta\right)\) …… (2)
Similarly applying the cosine law for triangle AOP,
r₂² = r² + a² – 2ra cos(180 – θ) since cos (180 – θ) = -cos θ we get
r₂² = r² + a² + 2ra cos θ
Neglecting the term \(\frac{a^{2}}{r^{2}}\) (because r >> a)

Using Binomial theorem, we get
\(\frac{1}{r_{2}}=\frac{1}{r}\left(1-a \frac{\cos \theta}{r}\right)\) ………. (3)
Substituting equations (3) and (2) in equation (1)

But the electric dipole moment p = 2qa and we get,
\(\mathrm{V}=\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{p \cos \theta}{r^{2}}\right)\)
Now we can write p cos θ = \(\vec{r}\) . r̂ where r̂ is the unit vector from the point O to point P.
Hence the electric potential at a point P due to an electric dipole is given by
V = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\vec{p} \cdot \hat{r}}{r^{2}}\) (r >> a) …(4)
Equation (4) is valid for distances very large compared to the size of the dipole. But for a point dipole, the equation (4) is valid for any distance.

Special cases:
Case (1) If the point P lies on the axial line of the dipole on the side of +q, then θ = 0. Then the electric potential becomes
\(V=\frac{1}{4 \pi \varepsilon_{0}} \frac{p}{r^{2}}\)

Case (ii) If the point Plies on the axial line of the dipole on the side of -q. then θ = 180°, then
\(\mathrm{V}=-\frac{1}{4 \pi \varepsilon_{0}} \frac{p}{r^{2}}\)

Case (iii) If the point P lies on the equatorial line of the dipole, then θ = 90°. Hence, V = 0.

Question 34.
(b) Explain the determination of the internal resistance of a cell using voltmeter.
Answer:
Determination of internal resistance: The emf of cell ξ is measured by connecting a high resistance voltmeter across it without connecting the external resistance R. Since the voltmeter draws very little current for deflection, the circuit may be considered as open. Hence, the voltmeter reading gives the emf of the ceíl. Then, external resistance R is included in the circuit and current I is established in the circuit. The potential difference across R is equal to the potential difference across the cell (V).

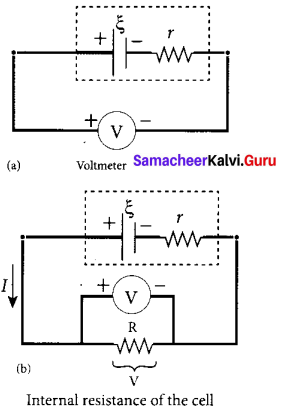
The potential drop across the resistor R is
V = IR …….. (1)

Due to internal resistance r of the cell, the voltmeter reads a value V, which is less than the emf of cell ξ. It is because, certain amount of voltage (Ir) has dropped across the internal resistance r.
Then V = ξ – Ir
Ir = ξ – V ……… (2)
Dividing equation (2) by equation (1), we get
\(\frac{I r}{I R}=\frac{\xi-V}{V}\)
\(r=\left|\frac{\xi-V}{V}\right| R\) ……… (3)
since ξ, V and R are known, internal resistance r can be determined

Question 35.
(a) Calculate the magnetic induction at a point on the axial line of a bar magnet.
Answer:
Magnetic field at a point along the axial line of the magnetic dipole (bar magnet): Consider a bar magnet NS. Let N be the North Pole and S be the south pole of the bar magnet, each of pole strength q, and separated by a distance of 2l. The magnetic field at a point C (lies along the axis of the magnet) at a distance from the geometrical center O of the bar magnet
can be computed by keeping unit north pole (q_MC = 1 A m) at C. The force experienced by the unit north pole at C due to pole strength can be computed using Coulomb’s law of magnetism as follows:
The force of repulsion between north pole of the bar magnet and unit north pole at point C (in free space) is
\(\overrightarrow{\mathrm{F}}_{\mathrm{N}}=\frac{\mu_{0}}{4 \pi} \frac{q_{m}}{(r-l)^{2}} \hat{l}\) …. (1)
where r – l is the distance between north pole of the bar magnet and unit north pole at C.
The force of attraction between South Pole of the bar magnet and unit North Pole at point C (in free space) is
\(\overrightarrow{\mathrm{F}}_{\mathrm{S}}=-\frac{\mu_{0}}{4 \pi} \frac{q_{m}}{(r+l)^{2}} \hat{l}\) ……. (2)
where r + l is the distance between South pole of the bar magnet and unit north pole at C.

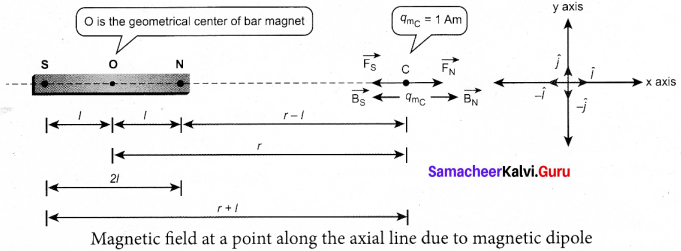
From equation (1) and (2), the net force at point C is \(\vec{F}\) = \(\vec{F}\)_N + \(\vec{F}\)_s . From definition, this net force is the magnetic field due to magnetic dipole at a point C (\(\vec{F}\) = \(\vec{B}\))

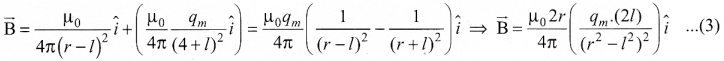
Since, magnitude of magnetic dipole moment is |\(\vec{P}\)_m| = P_m = q_m .2l the magnetic field point C equation (3) can be written as
\(\vec{B}\)_axial = \(\frac{\mu_{0}}{4 \pi}\left(\frac{2 r p_{m}}{\left(r^{2}-l^{2}\right)^{2}}\right) \hat{i}\) …… (4)
If the distance between two poles in a bar magnet are small (looks like short magnet) compared to the distance between geometrical centre O of bar magnet and the location of point C i.e.,
r >> l then (r² – l²)² ≈ r⁴ ……. (5)
Therefore, using equation (5) in equation (4), we get

[OR]

Question 35.
(b) Show mathematically that the rotation of a coil in a magnetic field over one rotation induces an alternating emf of one cycle.
Answer:
Induction of emf by changing relative orientation of the coil with the magnetic field:
Consider a rectangular coil of N turns kept in a uniform magnetic field \(\vec{B}\) figure (a). The coil rotates in anti-clockwise direction with an angular velocity co about an axis, perpendicular to the field.

At time = 0, the plane of the coil is perpendicular to the field and the flux linked with the coil has its maximum value Φ_m = BA (where A is the area of the coil).

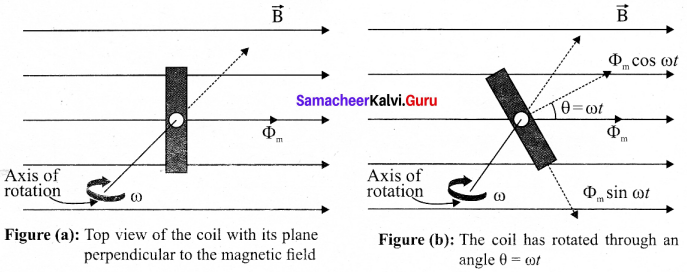
In a time t seconds, the coil is rotated through an angle θ (= ωt) in anti-clockwise direction. In this position, the flux linked is Φ_m cos ωt., a component of Φ_m normal to the plane of the coil (figure (b)). The component parallel to the plane (Φ_m sinωt) has no role in electromagnetic induction. Therefore, the flux linkage at this deflected position is NΦ_B = NΦ_m cos ωt. According to Faraday’s law, the emf induced at that instant is


ε = \(-\frac{d}{d t}\) (NΦ_B) = \(-\frac{d}{d t}\) (NΦ_m cos ωt)
= -NΦ_m (-sin ωt)ω = NΦ_m ω sin ωt
When the coil is rotated through 90° from initial position, sin ωt = 1. Then the maximum value of induced emf is
ε_m = NΦ_m ω = NBAω since Φ_m = BA
Therefore, the value of induced emf at that instant is then given by
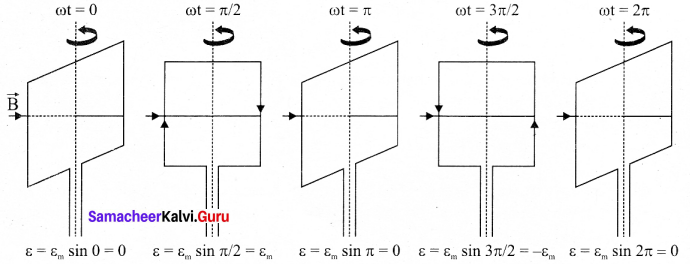
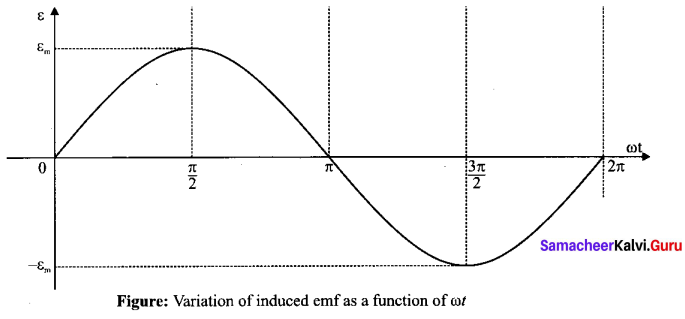
ε = ε_m sin ωt
It is seen that the induced emf varies as sin ωt function of the time angle ωt. The graph between induced emf and time angle for one rotation of coil will be a sine curve and the emf varying in this manner is called sinusoidal emf or alternating emf.

Question 36.
(a) Write down the properties of electromagnetic waves.
Answer:
Properties of electromagnetic waves:
1. Electromagnetic waves are produced by any accelerated charge.

2. Electromagnetic waves do not require any medium for propagation. So electromagnetic wave is a non-mechanical wave.

3. Electromagnetic waves are transverse in nature. This means that the oscillating electric field vector, oscillating magnetic field vector and propagation vector (gives direction of propagation) are mutually perpendicular to each other.

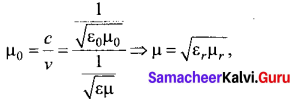
4. Electromagnetic waves travel with speed which is equal to the speed of light in vacuum or free space, c = \(\frac{1}{\sqrt{\varepsilon_{0} \mu_{0}}}\) = 3 × 10⁸ ms^-1

5. The speed of electromagnetic wave is less than speed in free space or vacuum, that is, v < c. In a medium of refractive index,

Question 36.
(b) Derive the equation for acceptance angle and numerical aperture, of optical fiber.
Answer:
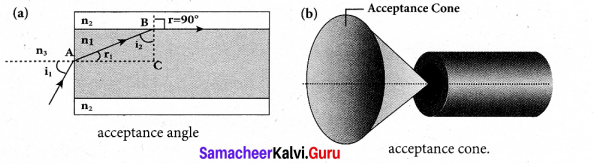
Acceptance angle in optical fibre:
To ensure the critical angle incidence in the core-cladding boundary inside the optical fibre, the light should be incident at a certain angle at the end of the optical fiber while entering in to it. This angle is called acceptance angle. It depends on the refractive indices of the core n₁ cladding n₂ and the outer medium n₃. Assume the light is incident at an angle i_a called acceptance angle i at the outer medium and core boundary at A.
The Snell’s law in the product form, equation for this refraction at the point A.

n₃ sin i_a = n₁ sin r_a …(1)
To have the total internal reflection inside optical fibre, the angle of incidence at the core-cladding interface at B should be atleast critical angle i_c . Snell’s law in the product form, equation for the refraction at point B is,
n₁ sin i_c = n₂ sin 90° …(2)
n₁ sin i_c = n₂ ∵ sin 90° = 1
∴ sin i_c = \(\frac{n_{2}}{n_{1}}\) …(3)
From the right angle triangle ∆ABC,
i_c = 90° – r_a
Now, equation (3) becomes, sin (90° – r_a) = \(\frac{n_{2}}{n_{1}}\)
Using trigonometry, cos r_a = \(\frac{n_{2}}{n_{1}}\) …(4)
sin r_a = \(\sqrt{1-\cos ^{2} r_{a}}\)
Substituting for cos r_a
sin r_a = \(\sqrt{1-\left(\frac{n_{2}}{n_{1}}\right)^{2}}=\sqrt{\frac{n_{1}^{2}-n_{2}^{2}}{n_{1}^{2}}}\) …… (5)
Substituting this in equation (1)
n₃ sin i_a = \(n_{1} \sqrt{\frac{n_{1}^{2}-n_{2}^{2}}{n_{1}^{2}}}=\sqrt{n_{1}^{2}-n_{2}^{2}}\) ….. (6)
On further simplification,

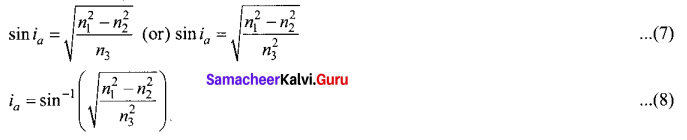
If outer medium is air, then n₃ = 1. The acceptance angle i_a becomes,
i_a = sin^-1\((\sqrt{n_{1}^{2}-n_{2}^{2}})\) …… (9)

Light can have any angle of incidence from 0 to i_a with the normal at the end of the optical fibre forming a conical shape called acceptance cone. In the equation (6), the term (n₃ sin i_a) is called numerical aperture NA of the optical fibre.
NA = n₃ sin i_a \((\sqrt{n_{1}^{2}-n_{2}^{2}})\) ….. (10)

If outer medium is air, then n₃ = 1. The numerical aperture NA becomes,
NA = sin i_a \(\sqrt{n_{1}^{2}-n_{2}^{2}}\) ….. (11)

Question 37.
(a) Explain the effect of potential difference on photoelectric current.
Answer:
Effect of potential difference on photoelectric current:
To study the effect of potential difference V between the electrodes on photoelectric current, the frequency and intensity of the incident light are kept constant. Initially the potential of A is kept positive with respect to C and the cathode is irradiated with the given light.

Now, the potential of A is increased and the corresponding photocurrent is noted. As the potential of A is increased, photocurrent is also increased. However a stage is reached where photocurrent reaches a saturation value (saturation current) at which all the photoelectrons from C are collected by A. This is represented by the flat portion of the graph between potential of A and photocurrent.

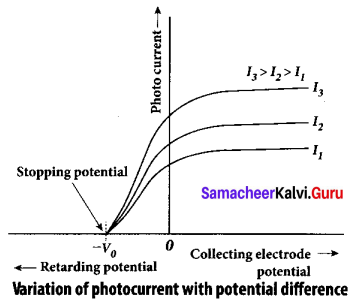
When a negative (retarding) potential is applied to A with respect to C, the current does not immediately drop to zero because the photoelectrons are emitted with some definite and different kinetic energies. .

The kinetic energy of some of the photoelectrons is such that they could overcome the retarding electric field and reach the electrode A.

When the negative (retarding) potential of A is gradually increased, the photocurrent starts to decrease because more and more photoelectrons are being repelled away from reaching the electrode A. The photocurrent becomes zero at a particular negative potential V₀ , called stopping or cut-off potential.

Stopping potential is that the value of the negative (retarding) potential given to the collecting electrode A which is just sufficient to stop the most energetic photoelectrons emitted and make the photocurrent zero.

At the stopping potential, even the most energetic electron is brought to rest. Therefore, the initial kinetic energy of the fastest electron (K_max) is equal to the work done by the stopping potential to stop it (eV₀).
K_max = \(\frac { 1 }{ 2 }\) mv²_maxK = eV₀ ……… (1)
where v_max is the maximum speed of the emitted photoelectron.

From equation (1),
K_max = eV₀ (in joule) (or) K_max – V₀ (in eV)

From the graph, when the intensity of the incident light alone is increased, the saturation current also increases but the value of V₀ remains constant.

Thus, for a given frequency of the incident light, the stopping potential is independent of intensity of the incident light. This also implies that the maximum kinetic energy of the photoelectrons is independent of intensity of the incident light.

[OR]

Question 37.
(b) Explain the J.J. Thomson experiment to determine the specific charge of electron.
Answer:
In 1887, J. J. Thomson made remarkable improvement in the scope of study of gases in discharge tubes. In the presence of electric and magnetic fields, the cathode rays are deflected. By the variation of electric and magnetic fields, mass normalized charge or the specific charge (charge per unit mass) of the cathode rays is measured.

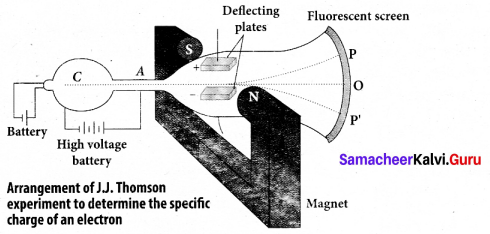
A highly evacuated discharge tube is used and cathode rays (electron beam) produced at cathode are attracted towards anode disc A. Anode disc is made with pin hole in order to allow only a narrow beam of cathode rays. These cathode rays are now allowed to pass through the parallel metal plates, maintained at high voltage. Further, this gas discharge tube is kept in between pole pieces of magnet such that both electric and magnetic fields are perpendicular to each other. When the cathode rays strike the screen, they produce scintillation and hence bright spot is observed. This is achieved by coating the screen with zinc sulphide.

(i) Determination of velocity of cathode rays
For a fixed electric field between the plates, the magnetic field is adjusted such that the cathode rays (electron beam) strike at the original position O. This means that the magnitude of electric force is balanced by the magnitude of force due to magnetic field. Let e be the charge of the cathode rays, then
eE eBv
⇒ ν = \(\frac{E}{B}\) …… (1)

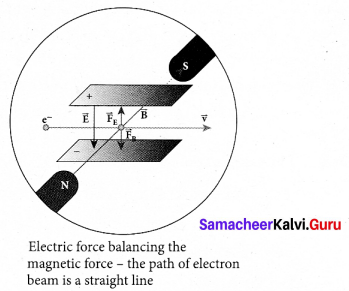
(ii) Determination of specific charge:
Since the cathode rays (electron beam) are accelerated from cathode to anode, the potential energy of the electron beam at the cathode is converted into kinetic energy of the electron beam at the anode. Let V be the potential difference between anode and cathode, then the potential energy is eV. Then from law of conservation of energy,
eV = \(\frac{1}{2}\)mV² ⇒ \(\frac{e}{m}=\frac{v^{2}}{2 \mathrm{V}}\)
Substituting the value of velocity from equation (1), we get
\(\frac{e}{m}=\frac{1}{2 \mathrm{V}} \frac{\mathrm{E}^{2}}{\mathrm{B}^{2}}\) ….. (2)
Substituting the values of E, B and V, the specific charge can be determined as
\(\frac{e}{m}\) = 1.7 × 10¹¹ C kg^-1

(iii) Deflection of charge only due to uniform electric field:
When the magnetic field is turned off, the deflection is only due to electric field. The deflection in vertical direction is due to the electric force.

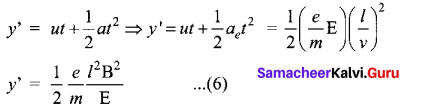
F_e = eE …(3)
Let m be the mass of the electron and by applying Newton’s second law of motion, acceleration of the electron is
a_e = \(\frac{1}{m}\) F_e ……. (4)
Substituting equation (4) in equation (3),
a_e = \(\frac{1}{m} e E=\frac{e}{m} E\)

Let y be the deviation produced from Deviation of path by applying uniform electric field original position on the screen. Let the initial upward velocity of cathode ray be u = 0 before entering the parallel electric plates. Let t be the time taken by the cathode rays to travel in electric field. Let l be the length of one of the plates, then the time taken is
t = \(\frac{1}{v}\) …(5)
Hence, the deflection y’ of cathode rays is (note: u = 0 and a_e = \(\frac{e}{m}\)E)

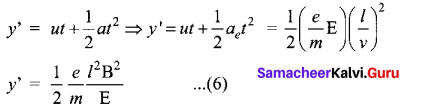
Therefore, the deflection y on the screen is
y ∝ y’ ⇒ y = Cy’
where C is proportionality constant which depends on the geometry of the discharge tube and substituting y’ value in equation (6), we get y = C \(\frac{1}{2} \frac{e}{m} \frac{l^{2} \mathrm{B}^{2}}{\mathrm{E}}\) ……. (7)
Rearranging equation (7) as \(\frac{e}{n}=\frac{2 y \mathrm{E}}{\mathrm{Cl}^{2} \mathrm{B}^{2}}\) …… (8)
Substituting the values on RHS, the value of specific charge is calculated as
\(\frac{e}{m}\) = 1.7 × 10¹¹Ckg^-1m

(iv) Deflection of charge only due to uniform magnetic field
Suppose that the electric field is switched off and only the magnetic field is switched on. Now the deflection occurs only due to magnetic field. The force experienced by the electron in uniform magnetic field applied perpendicular to its path is
F_m = evB (in magnitude)
Since this force provides the centripetal force, the electron beam undergoes a semicircular path. Therefore, we can equate F_m to centripetal force \(\frac{m v^{2}}{R}\)
F_m = evB = \(m \frac{v^{2}}{R}\)
where v is the velocity of electron beam at the point where it enters the magnetic field and R is the radius of the circular path traversed by the electron beam.
eB = \(m \frac{v}{\mathrm{R}} \Rightarrow \frac{e}{m}=\frac{v}{\mathrm{BR}}\) ……. (9)
Further, substituting equation (1) in equation (9), we get
\(\frac{e}{m}=\frac{E}{B^{2} R}\) …….. (10)
By knowing the values of electric field, magnetic field and the radius of circular path, the value of specific charge \(\left(\frac{e}{m}\right)\) can be calculated

Question 38.
(a) Draw the circuit diagram of a half wave rectifier and explain its working
Answer:
Half wave rectifier circuit:
The half wave rectifier circuit. The circuit consists of a transformer, a p-n junction diode and a resistor. In a half wave rectifier circuit, either a positive half or the negative half of the AC input is passed through while the other half is blocked. Only one half of the input wave reaches the output. Therefore, it is called halfwave rectifier. Here, a p-n junction diode acts as a rectifying diode.

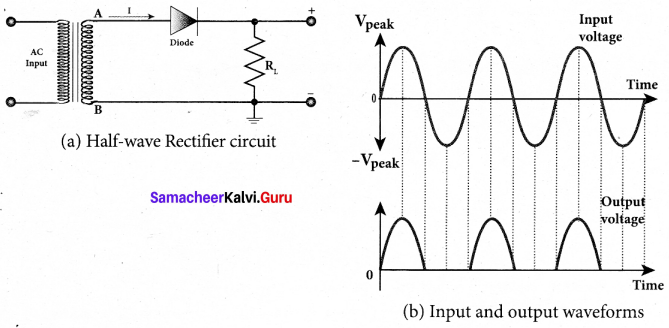
During the positive half cycle:
When the positive half cycle of the ac input signal passes through the circuit, terminal A becomes positive with respect to terminal B. The diode is forward biased and hence it conducts. The current flows through the load resistor R_L and the AC voltage developed across R_L constitutes the output voltage V₀ and the waveform of the diode current.

During the negative half cycle:
When the negative half cycle of the ac input signal passes through the circuit, terminal A is negative with respect to terminal B. Now the diode is reverse biased and does not conduct and hence no current passes through R_L. The reverse saturation current in a diode is negligible. Since there is no voltage drop across R_L, the negative half cycle of ac supply is suppressed at the output.

The output of the half wave rectifier is not a steady dc voltage but a pulsating wave. This pulsating voltage is not sufficient for electronic equipments. A constant or a steady voltage is required which can be obtained with the help of filter circuits and voltage regulator circuits. Efficiency (η) is the ratio of the output dc power to the ac input power supplied to the circuit. Its value for half wave rectifier is 40.6 %

[OR]

Question 38.
(b) Fiber optic communication is gaining popularity among the various transmission media – justify.
Answer:
The method of transmitting information from one place to another in terms of light pulses through an optical fiber is called fiber optic communication. It is in the process of replacing wire transmission in communication systems.
Light has very high frequency (400 THz – 790 THz) than microwave radio systems. The fibers are made up of silica glass or silicon dioxide which is highly abundant on Earth.
Now it has been replaced with materials such as chalcogenide glasses, fluoroaluminate crystalline materials because they provide larger infrared wavelength and better transmission capability.
As fibers are not electrically conductive, it is preferred in places where multiple channels are to be laid and isolation is required from electrical and electromagnetic interference.

Applications
Optical fiber system has a number of applications namely, international communication, inter¬city communication, data links, plant and traffic control and defense applications.

Merits

• Fiber cables are very thin and weight lesser than copper cables.
• This system has much larger bandwidth. This means that its information carrying capacity is larger.
• Fiber optic system is immune to electrical interferences.
• Fiber optic cables are cheaper than copper cables.

Demerits

• Fiber optic cables are more fragile when compared to copper wires.
• It is an expensive technology.